8大排序算法-我熟知一（冒泡、直接插入）

参考：https://itimetraveler.github.io/2017/07/18/%E5%85%AB%E5%A4%A7%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95%E6%80%BB%E7%BB%93%E4%B8%8Ejava%E5%AE%9E%E7%8E%B0/#四、堆排序（Heap-Sort）

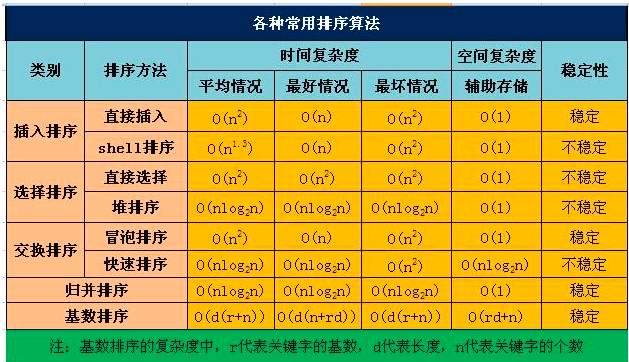
分类：

1）插入排序（直接插入排序、希尔排序）
2）交换排序（冒泡排序、快速排序）
3）选择排序（直接选择排序、堆排序）
4）归并排序
5）分配排序（基数排序）
所需辅助空间最多：归并排序
所需辅助空间最少：堆排序
平均速度最快：快速排序

不稳定：快速排序，希尔排序，堆排序。

1、冒泡算法(bubble)-  -属于交换排序 -- --o(n^2)

　　两两相邻元素比较，不符合就交换。直到最后没有可交互的元素。一趟排序下来，最大的元素在尾部,越小的元素会经由交换慢慢“浮”到数列的顶端。

冒泡排序算法的运作如下：

1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
3. 针对所有的元素重复以上的步骤，除了最后一个。
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

coding:

    public static void bubbleSort(int[] arr) {
    int i, j, temp, len = arr.length;
    for (i = 0; i < len - 1; i++) {
        for (j = 0; j < len - 1 - i; j++) {
            if (arr[j] > arr[j + 1]) {
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    } 
    }

优化的冒泡：

由于可能在前几次就已经排好序，但是在上一种冒泡排序中仍然需要一直遍历到最后。最坏情况为O（N^2）

优化措施：设置一个标志，如果这一趟发生了交换，则为true，否则为false。明显如果有一趟没有发生交换，说明排序已经完成。最坏的情况可以优化到O（n）

public void BubbleSort1(int[] a) {
        int temp = 0;
        int len = a.length;
        boolean flag = true;
        while (flag) {
            flag = false;
            for (int j = 1; j < len - 1; j++)
                if (a[j - 1] > a[j]) {
                    // 注意分清是a[j-1]还是a[j]不然容易出现边界问题
                    // 从小到大排序
                    temp = a[j - 1];
                    a[j - 1] = a[j];
                    a[j] = temp;
                    // 设置标志位
                    flag = true;
                }
        }
    }

2、直接插入

基本思想：将需要排序的关键数与前面已经排好序的数据从后往前进行比较，使其插入到合适的位置。

 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率；

coding: 

 public static void insertSort(int[] array) {
     for (int i = 1; i < array.length; i++) {
         int temp = array[i];
         int j = i - 1;
         for (; j >= 0 && array[j] > temp; j--) {
             //将大于temp的值整体后移一个单位
             array[j + 1] = array[j];
         }
         array[j + 1] = temp;
     }
     System.out.println(Arrays.toString(array) + " insertSort");
 }

 冒泡排序是与插入排序拥有相等的运行时间，但是两种算法在需要的交换次数却很大地不同。在最坏的情况，冒泡排序需要次交换，而插入排序只要最多交换。冒泡排序的实现（类似下面）通常会对已经排序好的数列拙劣地运行（），而插入排序在这个例子只需要{displaystyle O(n)}个运算。因此很多现代的算法教科书避免使用冒泡排序，而用插入排序取代之。

 3、