关于神经网络和逻辑回归的关系,学它们俩和编程的时候有点似懂非懂。这里尝试记录现在所体会整理到的感觉。结论本身没有科学研究的价值或意义,只是在编程和设计全连接神经网络时能带来一定程度的指导。
对于最经典的二分类逻辑回归。用一组二元的输入和它们各自对应的一个非0即1的输出,能将二元输入扩展为多项式求和形式,使用梯度下降或其它优化算法学习得到一组theta。
所使用的代价函数即对应梯度如图(含正则项):

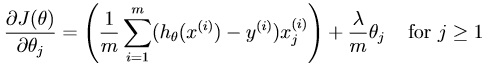
不管是代价函数还是梯度,我们都不对作为常数项或者稍后说的偏置项theta0进行正则化。使用矩阵能大幅简化运算。
为了有更直观的感受,我们考虑特殊情形:
假设有很多二元输入(x1,x2)的样本及其对应非0即1的输出y,我们使用每一个样本中的两个输入值(x1,x2)扩展出一个x1和x2至高6次方的多项式,也就是1+x1+x2+x1^2+x1x2+x2^2...+x1x2^5+x2^6,总计有28项(0次方一项,1次方两项...1+2+3+...+6+7=28)。
现在的输入变成了很多个28维度的行/列向量,最后只需要得到一个预测值并与阈值比较后判断原输入是否为目标类型。由于二分类逻辑回归使用的激励函数/预测函数是sigmoid,可以想见theta也应该有28项(不考虑转置的情况,单个输入为28*1的矩阵,最后需要得到一个标量,所以theta必为28*1矩阵)。
虽然有的地方说sigmoid值的意义并不是预测概率,但实际分类确实就是根据sigmoid值与阈值判断的,可以近似认为sigmoid值作用就是分类预测可信度。所以可以认为最后学习到的theta的作用是:对应于二分类问题中的目标类别,使用该theta与某样本输入进行逻辑回归预测,或者说代入到sigmoid函数中计算,就能得知该样本是否属于目标类。
二分类中这一意义的体现非常直观,接下来是多分类。
我所学习的多分类是基于OneVsAll的,这也确实是将逻辑回归从二分类推广到多分类问题最直接的做法。
多分类问题中,我们同样有一大堆输入,不同的是现在所给的输出不再是非0即1,而是有很多类别,不过仍可以用0-m的不同数字给这些类别编号。
按照OneVsAll的思想,我们应该依次将每一种类别都作为目标类别,与其它所有类别进行二分类逻辑回归。可见代价函数和梯度计算方法是不变的。
同样对于具体一点的例子,比如对一大堆20*20像素的手写数字图片,这些图像无非属于0-9这十个数中一个。这时候得到的theta是什么呢?
通常我们会把20*20总共400个像素点与一个偏置项“1”,写在一行或一列便于计算,这并不影响这个图像的含义,这时候这一行有401项的行/列向量就是一个单独的输入样本!稍加思考可以明白,我们将每一种类别作为目标类别,比如2,的时候,实际上仍然需要使用所有像这样处理了的输入样本进行学习。由上面二分类时的讨论可知,由于每次样本输入有401项,对于类别2,我们需要一行/列401项的theta来得到输入对于类别2的预测概率值。对于本例0-9每个类别都要学习这样的theta,所以需要10个401项的theta。这10个theta分别对应不同的类别。
对于一个新的1*401的输入,如果将它与每个有1*401项theta分别计算,则可以得到该输入对每个类别的概率。最后取概率最大值位置便是该输入所属类别。
虽然编程的时候这部分已经有点绕了,但也都还好,之后是神经网络。
神经网络的更细节的部分并不想在这篇文中阐述,我想记录的只是更直观感性的一点认知。神经网络的层与层之间到底在干什么。
一个单隐藏层的神经网络图如下:

直接用具体例子思考,输入输出仍然是上面多分类那样,给定一张20*20像素的手写数字图像判断其数字类别。对每幅图像的输入同样进行上面那样化为一行/列的处理,这里使用的神经网络依次需要401个输入层单元(对应每幅图像得到的401项输入),25个隐藏层单元(本例人为规定)和总类别数量决定的10个输出层单元。
由于全连接,我们可以发现对于输入层-隐藏层这一部分,对于每一个隐藏单元,都有401个单元指向它。整个输入-隐藏的层间需要25*401条权重,也就是theta的大小,这里表示为Theta1。而同样地,研究隐藏-输出这一部分的Theta2,我们需要10*26(25个单元+1个隐藏层偏置项)条权重,也就是Theta2大小为10*26。
将这种情况与多分类问题时对比,就可以得到一个对层间交互的感性认知:神经网络每两层之间都是一个多分类问题。这样编程时或许就不会再有“突然手足无措”的感觉。首先由原始输入得到它“属于”每个隐藏单元的概率,每经过一层就相当于用前一层的概率新构建了一个虚拟样本。同时,原始输入有401个项,虚拟样本则相当于只有26项,原始输入中难以发现的特征也在这过程中得到了概括和抽象,而最后一个隐藏层才计算得到对于每个分类的真正概率。