栈
导言
随着生活水平的不断提高,越来越多的轿车走进千家万户,不过这也带来了一个严重的问题——停车位的寻找变得困难,因此在生活中我们经常会遇到把车停在不应该停的位置,导致半夜接到电话要求挪车或者收了罚单。现在我们来想象一个情景,我要在一个只有一个出口的窄巷子停车,那么停在内部的车想要开出来,就必须等在最外面的车开走,新的车停进来,只能停在窄巷子的最外面,最里面的车想要开出来就必须让其他所有的车都开走。

这真是一种我们很不愿意见到的情景,好在现实中司机一般不会做这种事情。如果我们把这个窄巷子抽象成一个线性表,车当做表中的元素,我们会发现这个线性表只能对表尾操作,放入新的元素就必须从表尾放入,由于尾部的元素把表的唯一出口堵死了,因此想要把表中的元素拿出,就只能拿出表尾,即最后一个元素。那么这种特殊的顺序表就是一种新的数据结构——栈,它的特点是先进后出,后进先出。栈在计算机相关领域中使用广泛,举个大家熟悉的例子,例如浏览器的后退功能,同个这个按键,我们可以查看单个网页的页面之前查看过的连接,而且这个按键的操作也是单向的,后查看的链接会被先查看。

什么是栈?
栈(stack)又名堆栈,它是一种运算受限的线性表,受限于该结构仅能在表尾进行元素的插入和删除操作。首先栈本质上还是一个线性表,只是有一些操作上较为特殊,栈中的元素具有仍然具有线性关系。在允许进行插入和删除的一段被称之为栈顶,表的另一端被称为栈底,若在栈中没有任何元素,栈就被称为空栈,栈结构的插入操作被称为压栈,删除操作被称为退栈或出栈。栈最鲜明的特点就是先进后出,后进先出,出栈的元素一定是位于栈顶的元素,在栈顶的元素出栈之后,下一个元素就成为新的栈顶,当栈底的元素执行出栈操作之后栈就成为了空栈。

栈的抽象数据类型
ADT Stack
{
Data:
D = {ai | 1 ≤ i ≤ n, n ≥ 0, ai 为 ElemType 类型} //同线性表
Relation:
R = { <ai,ai+1> | ai,ai+1 ∈ D, i = 1, i ∈ (0,n)} //同线性表
Operation:
InitStack(&s); //初始化栈,开辟一个空间给栈 s
StackEmpty(*s); //判断栈是否为空栈,若为空栈返回 true,否则返回 false
Push(&s,e); //进栈操作,将元素 e 加入栈结构中并使其作为栈顶
Pop(&s,&e); //出栈操作,将位于栈顶的元素删除,并赋值给变量 e
GetTop(s,&e); //取栈顶操作,若栈不为空栈,返回栈顶元素并赋值给变量 e
ClearStack(&s); //清空栈,将栈中的所有元素清空,即将栈变为空栈
DestroyStack(&s); //销毁栈,将释放栈的空间
}
顺序栈及其基本操作
顺序栈
栈是一种特殊的线性表,也自然可以使用顺序存储结构来实现。在 CC++ 中,我们对于顺序存储往往使用数组来描述,因此我们需要为一个数组选择栈底和栈顶,为了方便描述空栈判定和栈满判定,我们使用下标为 0 的位置作为栈底,当栈顶的下标为数组元素上限时即为栈满,为了时刻定位栈顶的位置,需要定义一个栈顶指针作为游标来辅助。

顺序栈的结构体定义
#define MAXSIZE 100
typedef struct
{
ElemType data[MAXSIZE];
int top; //栈顶指针
}SqStack;
初始化栈
为一个新建立的栈 s 分配足够的空间,由于空栈没有任何元素,因此栈顶指针将初始化为 -1。
void InitStack(SqStack s)
{
s = new SqStack;
s->top = -1; //栈顶指针将初始化为 -1,表示没有任何元素
}

空栈判断
某个结构为空一直是一个显然而敏感的状态,如果不妥善处理就会出现严重的异常,就例如对空栈执行出栈操作,就会出现非法读取的情况。因此虽然空栈判断的代码简单,但是值得我们重视。函数在栈为空栈时返回 true,反之返回 false。
bool StackEmpty(SqStack *s)
{
if(s->top == -1)
{
return true;
}
return false;
}
进栈操作
由于栈是一种操作受限的线性表,因此进栈操作是其核心操作之一。进栈的关键在于只能在表尾进行插入,并且当栈的空间为满的时候,不能入栈。函数将在栈不为满栈的情况下,在栈顶指针 top 处插入元素 e 并使其自增 1,插入成功返回 true,否则返回 false。时间复杂度 O(1)。
bool Push(SqStack &s,ElemType e)
{
if(s->top == MAXSIZE - 1) //判断是否栈满
{
return false;
}
s->data[s->top++] = e; //入栈
return true;
}
出栈操作
同进栈,出栈也是很重要的操作,出栈的关键在于只能在表尾进行插入,并且当栈的空间为空的时候,不能出栈。函数将在栈不为空栈的情况下,将位于栈顶指针 top 处的元素出栈并赋值给变量 e ,top 需要并使其自减 1,退栈成功返回 true,否则返回 false。时间复杂度 O(1)。
bool Pop(SqStack &s,ElemType e)
{
if(StackEmpty(s)) //判断是否为空栈
{
return false;
}
e = s->data[s->top--]; //退栈
return true;
}
取栈顶操作
取栈顶操作与出栈操作不同的是,取栈顶操作只需把栈顶元素赋值给变量 e,无需对栈进行修改。时间复杂度 O(1)。
bool GetTop(SqStack &s,ElemType e)
{
if(StackEmpty(s)) //判断是否为空栈
{
return false;
}
e = s->data[s->top]; //取栈顶
return true;
}
链栈及其基本操作
链栈
当栈使用链式存储结构来存储时,可以建立单链表来描述,显然以链表的表头结点作为栈顶是最方便的。使用连式存储结构的优点在于,栈的空间在一般情况下不需要考虑上限。对于链栈来说,我们可以不设置头结点。

链栈的结构体定义
typedef struct StackNode
{
ElemType data;
struct StackNode *next;
}Node,*Stack;
初始化栈
初始化的操作是为了构造一个空栈,在不设置头结点的情况下,我们把栈顶指针搞成 NULL 即可。
bool InitStack(Stack &s)
{
s = NULL;
return true;
}
空栈判断
某个结构为空一直是一个显然而敏感的状态,如果不妥善处理就会出现严重的异常,就例如对空栈执行出栈操作,就会出现非法读取的情况。因此虽然空栈判断的代码简单,对于链栈值得我们重视。函数在栈为空栈时返回 true,反之返回 false。
bool StackEmpty(Stack *s)
{
if(s == NULL)
{
return true;
}
return false;
}
进栈操作
对于链栈的进栈操作,我们不需要判断是否出现栈满的情况,只需要用头插法引入新结点即可,插入成功返回 true,否则返回 false。时间复杂度 O(1)。
bool Push(Stack &s,ElemType e)
{
Stack ptr = new Node; //为新结点申请空间
ptr->next = s; //修改新结点的后继为 s 结点,入栈
ptr->data = e;
s = ptr; //修改栈顶为 ptr
return true;
}

出栈操作
同顺序栈,当栈的空间为空的时候,不能出栈,函数将在栈不为空栈的情况下,需要把栈顶结点的空间释放掉,退栈成功返回 true,否则返回 false。时间复杂度 O(1)。
bool Pop(Stack &s,ElemType e)
{
Stack ptr;
if(StackEmpty(s)) //判断是否为空栈
{
return false;
}
e = s->data; //将栈顶元素赋值给 e
ptr = S; //拷贝栈顶元素
S = S->next; //退栈
delete ptr; //释放原栈顶元素结点的空间
return true;
}

取栈顶操作
当栈非空时,把栈顶元素赋值给变量 e,时间复杂度 O(1)。
bool GetTop(SqStack &s,ElemType e)
{
if(StackEmpty(s)) //判断是否为空栈
{
return false;
}
e = s->data; //取栈顶
return true;
}
双端栈
实现目标

复杂的操作由基本操作组合而成
我们这么去理解,假设我们已经定义了两个栈,开辟了一定的空间,那么会不会出现一个栈满了,而另一个栈还有很多空间呢?那么我们在这个时候就很希望能够让第一个栈使用第二个栈的空间,从理论上讲,这样是完全可行的,因为我们只需要让这两个栈能够分别找到自己的栈顶和栈底即可。例如在一个数组中,我们可以让数组的始端和末端分别为两个栈的栈底,再通过操作游标来实现对栈顶的描述。对于栈满的判断呢?只要两个栈的栈顶不见面,栈就不为满栈。



代码实现
建立双端栈
Stack CreateStack(int MaxSize) //建立双端栈
{
Stack sak = (Stack)malloc(sizeof(struct SNode));
sak->MaxSize = MaxSize;
sak->Data = (ElementType*)malloc(MaxSize * sizeof(ElementType));
sak->Top1 = -1;
sak->Top2 = MaxSize;
return sak;
}
入栈操作
bool Push(Stack S, ElementType X, int Tag) //入栈
{
if (S->Top2 - 1 == S->Top1)
{
printf("Stack Full
");
return false;
}
if (Tag == 1)
{
S->Data[++S->Top1] = X;
}
else
{
S->Data[--S->Top2] = X;
}
return true;
}
出栈操作
ElementType Pop(Stack S, int Tag) //出栈
{
if (Tag == 1)
{
if (S->Top1 < 0)
{
printf("Stack %d Empty
",Tag);
return ERROR;
}
else
{
return S->Data[S->Top1--];
}
}
else
{
if (S->Top2 == S->MaxSize)
{
printf("Stack %d Empty
",Tag);
return ERROR;
}
else
{
return S->Data[S->Top2++];
}
}
}
栈的应用
符号配对
应用情景

情景分析
由于我们只关注表达式的括号是否是成双成对的,因此只需要获取我们所需即可。当我获取第一个括号时,虽然后面可能会有贼多括号,但是我们只继续接受下一个括号,若下一个括号仍然为左括号,那么这个括号需要配对的优先级是高于第一个左括号的。继续读取,若下一个括号为右括号,就拿来和配对优先级较高的第二个括号比对,若成功配对则消解第二个括号,而第一个括号需要配对的优先级就提升了。经过分析我们发现,使用栈结构来描述这个过程极为合适。
伪代码

代码实现
#include <iostream>
#include <stack>
#include <string>
using namespace std;
int main()
{
string equation;
stack<char> brackets; //存储被配对的左括号
int flag = 0;
cin >> equation;
for (int i = 0; equation[i] != 0; i++)
{
if (equation[i] == '(' || equation[i] == '[' || equation[i] == '{') //第 i 个字符是左括号
{
brackets.push(equation[i]);
}
else if (brackets.empty() && (equation[i] == ')' || equation[i] == ']' || equation[i] == '}'))
{
flag = 1; //第 i 个字符是右括号但栈是空栈
break;
}
else if (equation[i] == ')' && brackets.top() == '(') //栈顶括号与右括号配对
{
brackets.pop();
}
else if (equation[i] == ']' && brackets.top() == '[')
{
brackets.pop();
}
else if (equation[i] == '}' && brackets.top() == '{')
{
brackets.pop();
}
}
if (flag == 1) //输出配对结果
{
cout << "no";
}
else if (brackets.empty() == true)
{
cout << "yes";
}
else
{
cout << brackets.top() << "
" << "no";
}
return 0;
}
逆波兰式的转换
逆波兰式
众所周知,对于一个算式而言,不同的运算符有优先级之分,例如“先乘除,后加减”,如果是我们人工进行计算的话,可以用肉眼观察出算式的运算顺序进行计算。可是对于计算机而言,如果是一个一个读取算式进行计算的话,可能不能算出我们想要的答案,因为这么做是没有优先级可言的。想要让计算机实现考虑优先级的算式计算,我们首先要先找到一种算式的描述方式,这种方式不需要考虑运算符优先级。
逆波兰式(Reverse Polish notation,RPN,或逆波兰记法),也叫后缀表达式(将运算符写在操作数之后的表达式),是波兰逻辑学家卢卡西维奇提出的,例如“2 + 3 * (7 - 4) + 8 / 4”这样一个表达式,它对应的后缀表达式是“2 3 7 4 - * + 8 4 / +”,这种表达式的计算方法是遇到运算符就拿前面的两个数字来计算,用这个数字替换掉计算的两个数字和运算符,直到得出答案。
应用情景

伪代码

代码实现
#include <iostream>
#include <stack>
#include <queue>
#include <string>
#include <map>
using namespace std;
int main()
{
string str;
stack<char> sign; //存储符号
queue<char> line; //存储转换好的逆波兰式,便于后续实现计算
map<char, int> priority;
priority['('] = 3; //为符号设置优先级
priority[')'] = 3;
priority['*'] = 2;
priority['/'] = 2;
priority['+'] = 1;
priority['-'] = 1;
int flag = 0;
cin >> str;
for (int i = 0; i < str.size(); i++)
{ //读取到数字
if (((i == 0 || str[i - 1] == '(') && (str[i] == '+' || str[i] == '-')) || (str[i] >= '0' && str[i] <= '9'))
{
line.push('#');
if (str[i] != '+')
{
line.push(str[i]);
}
while ((str[i + 1] >= '0' && str[i + 1] <= '9') || str[i + 1] == '.')
{
line.push(str[++i]);
}
}
else //读取到运算符
{
if (str[i] == ')') //运算符是右括号
{
while (!sign.empty() && sign.top() != '(') //左括号之后的运算符全部出栈
{
line.push('#');
line.push(sign.top());
sign.pop();
}
sign.pop();
continue;
}
else
{
while (!sign.empty() && sign.top() != '(' && priority[str[i]] <= priority[sign.top()])
{
line.push('#');
line.push(sign.top());
sign.pop();
}
}
sign.push(str[i]);
}
}
while (!sign.empty()) //将栈内剩余的符号出栈
{
line.push('#');
line.push(sign.top());
sign.pop();
}
while (!line.empty())
{
if (flag == 0 && line.front() == '#')
{
flag++;
}
else if(line.front() == '#')
{
cout << ' ';
}
else
{
cout << line.front();
}
line.pop();
}
return 0;
}
迷宫寻路(深度优先)
应用情景
例如如图所示迷宫,黄色方格代表起点,橙色方格代表终点,绿色方格代表可走路径,蓝色方格代表障碍物。已知这是一个 M × N 大小的迷宫,可以用 0 表示可走路径,1 表示障碍,算法要求实现从迷宫的任意一点出发,试探出一条通向终点的路径。

应用解析
刚看到这个情景,我们是一头雾水的,因此在开始解析之前,我们先把迷宫的构成说明白。如图是一个我已经鸽了很久的 RPG 游戏制作页面,我们发现这个页面和游戏的界面是不一样的,游戏的舞台被一个个方格所切割,制作这类的游戏时,我无论是绘制地图、设置事件还是踩雷遇怪,都是通过对这些方格填充内容实现的,而这些方格在一张确定大小的地图上都是有对应坐标的。

我们是怎么定位可控角色在地图的位置的?其实也是通过这些坐标,确定好角色所在的方格之后就把角色的贴图填充进去。当角色进行移动时,我们先获取这个角色的坐标,确定移动到哪个方格之后,播放设置好的行走图即可实现。不知道爱玩游戏的你是否想过这些问题呢?(笑)

现在我们已经把背景说明白了,再来思考一下,我们可以把需求的迷宫描述为一个二维数组,二维数组抽象成几何图形的时候是一个矩阵,因此我们的问题就变成了描述起点到终点坐标的问题了。这个时候我们就要模拟一个玩家,这个玩家要标记他走过的坐标,由于要自动寻路,有东南西北四个维度,因此我们就以这个顺序先作为玩家的寻路顺序。当玩家遇到死路时,就要退回之前走过的路,因此我们就发现了栈结构“后进先出”的特性很适合用于描述走回头路的过程。
代码实现
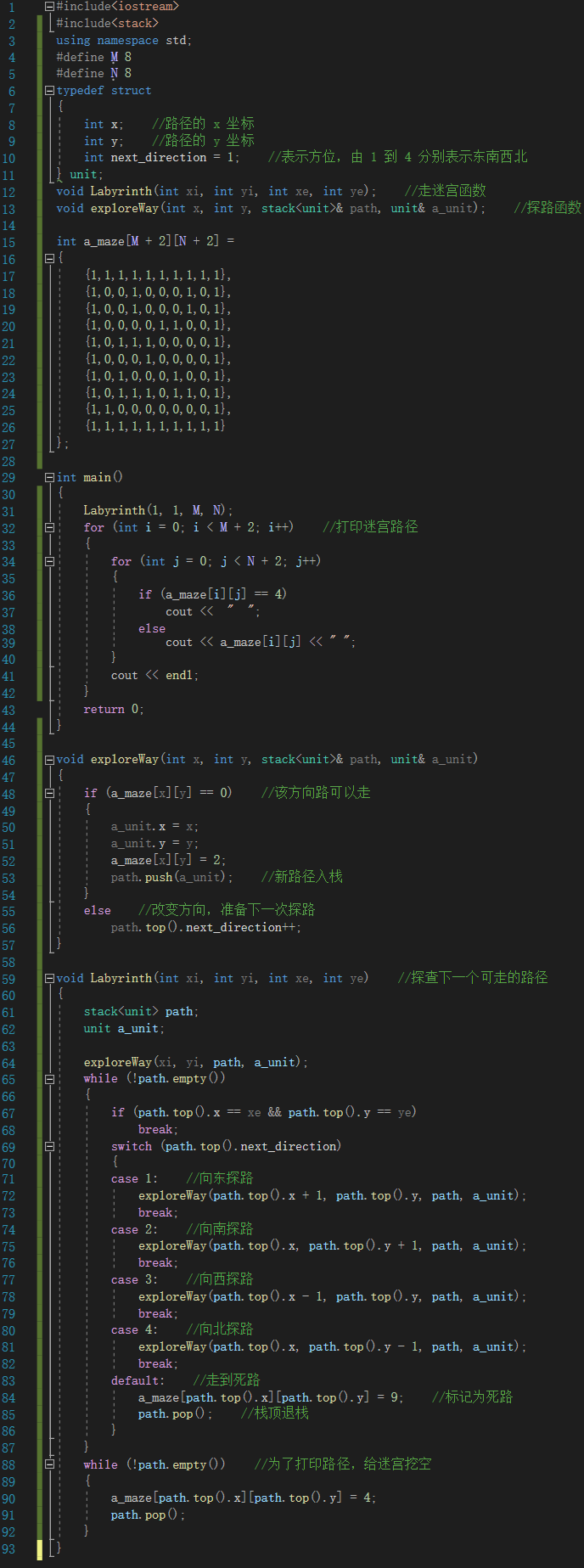
运行效果

- 虽然这段代码是以深度优先搜索为基础写出来的,但是这并不完整,因为理论上深度优先搜索是可以找到所有路径的。解决方案是找到终点之后仍然走回头路,在有岔路的地方再次进行试探,直到没有岔路可走为止。此处只是为了展示栈结构的应用,深度优先搜索并不是我们当前要谈的问题,因此我简化的操作,并且将路径挖空,帮助我们更好地理解。如果你想感受下“深度优先搜索”的话,请继续阅读下面的八皇后问题。
八皇后问题(栈实现)
左转我另一篇博客八皇后问题——回溯法思想运用
队列
导言
队列在生活中处处可见,例如在食堂买饭,你需要排队,先来的同学先买,后面的同学需要等前面的同学买好才能够前进(这不废话吗)。对于程序设计,队列的思想应用广泛,例如在操作系统中的作业排队也是使用队列来实现的,在一个允许多道程序运行的计算机系统中,面对多个运行的作业,它们就需要按照请求输入的次序排队,当通道阐述完毕时,队头的作业就先出队列进行输出操作。

什么是队列?
有别于栈,队列 (queue) 是只允许在一端进行插入操作,在另一端进行删除操作的线性表,核心思想是先进先出,其中允许插入操作的一端被称为队尾 (rear),允许删除操作的一端被称为队头 (front)。

队列的抽象数据类型
ADT Queue
{
Data:
D = {ai | 1 ≤ i ≤ n, n ≥ 0, ai 为 ElemType 类型} //同线性表
Relation:
R = { <ai,ai+1> | ai,ai+1 ∈ D, i = 1, i ∈ (0,n)} //同线性表
Operation:
InitQueue(&q); //初始化队列,开辟一个空间给队列 q
QueueEmpty(*q); //判断栈是否为空队列,若为空队列返回 true,否则返回 false
EnQueue(&q,e); //入队列操作,将元素 e 加入队列结构中并使其成为队尾元素
DeQueue(&q,&e); //出队列操作,将位于队列头的元素删除,并赋值给变量 e
GetHead(q,&e); //取队头操作,若栈不为空队列,返回队列头元素并赋值给变量 e
ClearQueue(&q); //清空队列,将栈中的所有元素清空,即将队列变为空队列
DestroyQueue(&q); //销毁队列,将释放队列的空间
QueueLength(q); //返回队列元素个数
}
顺序队列及其基本操作
假溢出
与顺序栈相似,由于队列本质上也是个线性表,因此我们对于顺序存储往往使用数组来描述,因此我们需要为一个数组设置队列头和队列尾,需要分别定义队头、队尾指针作为游标来辅助。初始化时,我们令 front = rear = 0,每当有元素入队列时,尾指针 rear 增加1,有元素出队列时,头指针 front 增加1,这样就能保证头指针始终指向队列头元素,尾指针始终指向队列尾元素,这样队列的头尾就说清楚了。
顺序队列的结构体定义
#define MAXSIZE 100
typedef struct
{
ElemType data[MAXSIZE];
int front; //队列头指针
int rear; //队列尾指针
}SqQueue;
但是这样会出现一个很严重的问题,假设有如图所示队列(MAXSIZE = 5),我们入队 5 个元素,然后出队 4 个元素,那么队列的状态就会变为图示的状态,此时如果继续有元素入队的话,就会因数组越界而发生溢出的情况,但是我们发现队列还是有很多的空闲空间的,这就说明我们的对列空间没有得到充分的利用,这是由“队尾入队,对头出队”的操作限制引起的。

顺序队列
对于假溢出问题,解决的思路很明确,就是我们需要实现某种机制让我们能回到数组下标为 0 的位置继续使用空闲的空间即可,也就是说我们需要一些代码让我们的队头指针和队尾指针复位,由于数组的长度我们可知,因此我们可以通过取模的方式来实现这种操作。当我们使用这种方法解决假溢出的问题时,这种队列结构也被称为循环队列,但是其本质只是添加了复位功能的队列而已。

如何判断空队列
因此可见,对于一个循环队列我们不能单纯地使用头指针或尾指针的值来描述空队列,对于这个问题有两种解决方案:
- 少使用一个数组空间,也就是说当数组中的元素数量达到 MAXSIZE - 1 时就认为是队列满,采用这种机制时,头尾指针数值相同时认为是空队列:
Q.front = Q.rear;
而尾指针数值加1之后等于头指针的数值时,认为队满:
(Q.rear + 1) % MAXSIZE == Q.front;
2.设置一个标志位来盘对是否为空队列。
初始化队列
构造一个空队列,分配一个最大容量是 MAXSIZE 的数组空间,头指针和尾指针的初始化为0,表示这是空队列。
void InitQueue(Queue &q)
{
q = new SqQueue;
q->front = q->reat = 0;
}
求队列长度
由于我们使用循环队列的描述方式,因此尾指针的值可能比头指针的数值小,也就是说尾指针与头指针的数值之差可能是负数,因此就需要对这个差值加上 MAXSIZE 之后对 MAXSIZE 求余。
int QueueLength(SqQueue q)
{
return (q.rear - q.front + MAXSIZE) % MAXSIZE;
}
入队列
在队尾插入一个新元素,若队满则无法插入,返回 false,否则返回 true。
bool EnQueue(SqQueue &q,ElemType e)
{
if((q,rear + 1) % MAXSIZE == q.front) //判断是否队列满
{
return false;
}
q.data[q.rear] = e;
q.rear = (q.rear + 1) % MAXSIZE;
return true;
}
出队列
将队列头的元素删除并赋值给 e,若为空队列则返回 false,否则返回 true.
bool DnQueue(SqQueue &q,ElemType e)
{
if(q.front == q.rear) //判断是否为空队列
}
取队列头元素
ElemType GetHead(SqQueue q)
{
if(q.front != q.rear) //判断是否是空队列
return q.data[q.front];
}
链队列
对于用链表描述的队列,我们需要两个指针分别指向队列头和队列尾,为了便于描述我们将添加一个头结点,用头指针指向。

链队列的结构体定义
typedef struct QueueNode
{
ElemType data;
struct QueueNode *next;
}Node,*QueuePtr;
typedef struct
{
QueuePtr front; //头指针
QueuePtr rear; //尾指针
}LinkQueue;
初始化队列
构造一个只有头结点的空队列,头指针和尾指针均指向头结点,头结点的指针域为 NULL。
void InitQueue(LinkQueue &q)
{
q.front = q.rear = new Node; //头指针和尾指针均指向头结点
q.front->next = NULL; //头指针的后继为 NULL
}

入队列
申请一个新结点,新结点的数据域为 e,通过尾插法的方式插入链队列中。对于链队列而言,不需要判断是否队满。
bool EnQueue(LinkQueue &q,ElemType e)
{
QueuePtr ptr = new Node;
if(ptr = NULL)
{
return false;
}
ptr->data = e;
ptr->next = NULL;
q.rear->next = ptr; //尾插法插入结点
q.rear = ptr; //修改尾指针
return true;
}

出队列
将链队列的表头结点的空间释放,若为空队列返回 false,否则返回 true。
bool DnQueue(LinkQueue &q,ElemType e)
{
QueuePtr ptr;
if(q.front == q,rear) //判断是否是空队列
return false;
ptr = q.front->next;
e = ptr->data;
q.front->next = ptr->next; //修改头结点的后继
if(q,rear == p) //若出队列操作后,队列为空队列,令尾指针指向头结点
q.rear = q.front;
delete ptr;
return true;
}

准确描述头尾指针
实现目标

应用解析
在不设置尾指针的情况下,我们该这么描述尾指针呢?如果你对尾指针和头指针存在的意义理解透彻的话,你就能明白,队列中的元素个数我们用“(q.rear - q.front + MAXSIZE) % MAXSIZE”来描述,现在我们只是需要反过来实现而已。
代码实现
入队列
bool AddQ(Queue Q, ElementType X)
{
if (Q->MaxSize == Q->Count)
{
printf("Queue Full
");
return false;
}
Q->Count++;
Q->Data[(Q->Front + Q->Count) % Q->MaxSize] = X;
return true;
}
出队列
ElementType DeleteQ(Queue Q)
{
if (Q->Count == 0)
{
printf("Queue Empty
");
return ERROR;
}
Q->Count--;
Q->Front = (Q->Front + 1) % Q->MaxSize;
return Q->Data[Q->Front];
}
队列应用
舞伴问题
应用情景

代码实现
int QueueLen(SqQueue Q) //取队列长度
{
return (Q->rear - Q->front);
}
int EnQueue(SqQueue& Q, Person e) //入队列
{
Q->data[Q->rear++] = e;
return 1;
}
int QueueEmpty(SqQueue& Q) //判断空队列
{
return !(Q->rear - Q->front);
}
int DeQueue(SqQueue& Q, Person& e) //出队列
{
e = Q->data[Q->front++];
return 1;
}
void DancePartner(Person dancer[], int num) //舞伴配对
{
Person people[2];
for (int i = 0; i < num; i++)
{
if (dancer[i].sex == 'F')
{
EnQueue(Fdancers, dancer[i]);
}
else
{
EnQueue(Mdancers, dancer[i]);
}
}
while (!QueueEmpty(Mdancers) && !QueueEmpty(Fdancers))
{
DeQueue(Fdancers, people[0]);
DeQueue(Mdancers, people[1]);
cout << people[0].name << " " << people[1].name << endl;
}
}

银行排队模拟
左转我的另一篇博客——PTA习题解析——银行排队问题
迷宫寻路(广度优先)
例如如图所示迷宫,黄色方格代表起点,橙色方格代表终点,绿色方格代表可走路径,蓝色方格代表障碍物。已知这是一个 M × N 大小的迷宫,可以用 0 表示可走路径,1 表示障碍,算法要求实现从迷宫的任意一点出发,试探出一条通向终点的路径。

应用解析
在这里我们想利用广度优先的思想来实现,本算法的思想是从 (xi,yi) 开始,利用队列的特点,一层一层扩大搜索的直径,把可走的点都导入到队列中,直到搜索到终点。
不过我这里主要是为了展示队列的应用,因此对于广度优先我在这里不过多阐述,可以自行查阅相关资料理解。这里需要强调的是,由于我们需要得到完整的路径,也就是说搜索过的路径不能够真出队列,以便于我们得到答案,因此就不能使用 STL 库的 queue 容器来实现,自建队列的话就要使用顺序队列来描述。不过我认为此处最适合的是 STL 库的 vector 容器,我们只需要定义两个游标来描述 vector 对象的队列头和尾的位置,就可以使用 vector 的方法来实现插入等操作,我们在解决银行排队问题的时候也是这么做的。
代码实现
#include<iostream>
#include<vector>
using namespace std;
#define M 8
#define N 8
typedef struct
{
int x;
int y; //路径的坐标
int pre; //表示该路径前驱的游标
} unit;
int exploreWay(int x, int y, vector<unit>& path, unit& a_unit, int front, int& rear); //添加单个路径
void Labyrinth(int xi, int yi, int xe, int ye, vector<unit>& min_path); //路径搜索函数
int a_maze[M + 2][N + 2] =
{
{1,1,1,1,1,1,1,1,1,1},
{1,0,0,1,0,0,0,1,0,1},
{1,0,0,1,0,0,0,1,0,1},
{1,0,0,0,0,1,1,0,0,1},
{1,0,1,1,1,0,0,0,0,1},
{1,0,0,0,1,0,0,0,0,1},
{1,0,1,0,0,0,1,0,0,1},
{1,0,1,1,1,0,1,1,0,1},
{1,1,0,0,0,0,0,0,0,1},
{1,1,1,1,1,1,1,1,1,1}
};
int main()
{
vector<unit> min_path; //存储最短路径
Labyrinth(1,1, M, N,min_path);
cout << "最短路径为:" << endl;
for (int i = min_path.size() - 1; i >= 0; i--)
{
cout << "(" << min_path[i].x << " , " << min_path[i].y << ") ";
if ((min_path.size() - i) % 5 == 0)
cout << endl;
}
return 0;
}
int exploreWay(int x, int y, vector<unit>& path, unit& a_unit, int front, int& rear)
{
if (a_maze[x][y] == 0) //若路径可走
{
a_unit.x = x;
a_unit.y = y;
a_unit.pre = front;
path.push_back(a_unit); //添加路径
rear++; //移动尾指针
a_maze[x][y] = 2;
return 1;
}
return 0;
}
void Labyrinth(int xi, int yi, int xe, int ye, vector<unit>& min_path) //搜索路径为:(xi,yi)->(xe,ye)
{
vector<unit> path; //存储所有可走路径
unit a_unit;
int front, rear = -1;
front = rear;
exploreWay(xi, yi, path, a_unit, front, rear); //添加起点路径,同时初始化头尾指针
while (rear != front)
{
front++; //判断路径东侧结点是否添加
if (exploreWay(path[front].x + 1, path[front].y, path, a_unit, front, rear) == 1
&& a_unit.x == xe && a_unit.y == ye)
break; //判断路径南侧结点是否添加
if (exploreWay(path[front].x, path[front].y + 1, path, a_unit, front, rear) == 1
&& a_unit.x == xe && a_unit.y == ye)
break; //判断路径西侧结点是否添加
if (exploreWay(path[front].x - 1, path[front].y, path, a_unit, front, rear) == 1
&& a_unit.x == xe && a_unit.y == ye)
break; //判断路径北侧结点是否添加
if (exploreWay(path[front].x, path[front].y - 1, path, a_unit, front, rear) == 1
&& a_unit.x == xe && a_unit.y == ye)
break;
}
while (rear != -1) //将搜索到的最短路径移动到 min_path
{
min_path.push_back(path[rear]);
rear = path[rear].pre;
}
}
运行效果

优先级队列
阅读代码部分,左转我另一篇博客数据结构——堆
参考资料
《大话数据结构》—— 程杰 著,清华大学出版社
《数据结构教程》—— 李春葆 主编,清华大学出版社
《数据结构与算法》—— 王曙燕 主编,人民邮电出版社
《数据结构(C语言版|第二版)》—— 严蔚敏 李冬梅 吴伟民 编著,人民邮电出版社