[bzoj1375] [Baltic2002] Bicriterial routing 双调路径

Description

如今的道路收费发展很快。道路的密度越来越大，因此选择最佳路径是很现实的问题。城市的道路是双向的，每条道路有固定的旅行时间以及需要支付的费用。
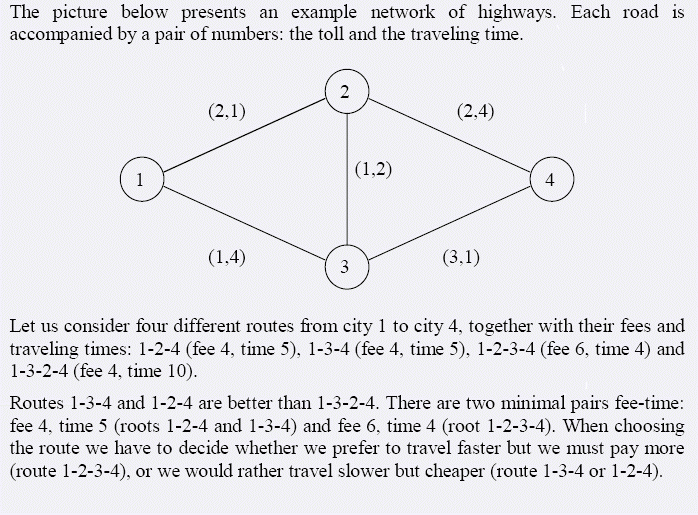
路径是连续经过的道路组成的。总时间是各条道路旅行时间的和，总费用是各条道路所支付费用的总和。一条路径越快，或者费用越低，该路径就越好。严格地说，如果一条路径比别的路径更快，而且不需要支付更多费用，它就比较好。反过来也如此理解。如果没有一条路径比某路径更好，则该路径被称为最小路径。
这样的最小的路径有可能不止一条，或者根本不存在路径。
问题：读入网络，计算最小路径的总数。费用时间都相同的两条最小路径只算作一条。你只要输出不同种类的最小路径数即可。

Input

第一行有四个整数，城市总数 (n)，道路总数 (m)，起点和终点城市 (s),(e)；
接下来的 (m) 行每行描述了一条道路的信息，包括四个整数，两个端点 (p),(r)，费用 (c)，以及时间 (t)；
两个城市之间可能有多条路径连接。

Output

仅一个数，表示最小路径的总数。

Sample Input

4 5 1 4

2 1 2 1

3 4 3 1

2 3 1 2

3 1 1 4

2 4 2 4

Sample Output

2

HINT

---

题解

首先，题目中对最小路径的描述有些歧义，实际上最小路径 (u) 应满足不存在路径 (v) 使 (cost[v] leq cost[u])，(len[v] leq len[u])
这可以说是一道 (DP) 题，也可以说是一道分层图 (SPFA)（本质是一样的）

分层图 (SPFA) 要好写一些。
设 (f[i][j]) 表示走到第 (i) 个结点，费用为 (j) 时的最短路
“转移”就是 (f[k][j+cost]=min(f[k][j+cost],f[i][j]+len)) ，不断更新

之后类似二维偏序，用树状数组就行了。

---

代码

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 105;
typedef pair<int,int> P;

struct node {
	int v,len,cost;
	node *next;
}pool[N*6],*h[N];
int cnt;
void addedge(int u,int v,int len,int cost){
	node *p=&pool[++cnt],*q=&pool[++cnt];
	p->v=v;p->next=h[u];h[u]=p;p->len=len;p->cost=cost;
	q->v=u;q->next=h[v];h[v]=q;q->len=len;q->cost=cost;
}

int n,m,s1,s2,S,T;
int f[N][N*N],vis[N][N*N];
queue<P> que;
void spfa(){
	for(int i=1;i<=n;i++)
		for(int j=0;j<=s1;j++) f[i][j]=1e8;
	f[S][0]=0; vis[S][0]=1; que.push(P(S,0));
	while(!que.empty()){
		int u=que.front().first,c=que.front().second,v;
		que.pop();
		vis[u][c]=0;
		s2=max(s2,f[u][c]);
		if(u==T) continue;
		for(node *p=h[u];p;p=p->next)
			if(c+p->cost<=s1 && f[v=p->v][c+p->cost]>f[u][c]+p->len){
				f[v][c+p->cost]=f[u][c]+p->len;
				if(!vis[v][c+p->cost]){
					vis[v][c+p->cost]=1;
					que.push(P(v,c+p->cost));
				}
			}
	}
}

int d[N*N];
int lowbit(int x) { return x&(-x); }
int add(int x,int y){
	while(x<=s2){
		d[x]+=y;
		x+=lowbit(x);
	}
}
int sum(int x){
	int ret=0;
	while(x){
		ret+=d[x];
		x-=lowbit(x);
	}
	return ret;
}

int main()
{
	int x,y,len,c,ans=0;
	scanf("%d%d%d%d",&n,&m,&S,&T);
	for(int i=0;i<m;i++){
		scanf("%d%d%d%d",&x,&y,&c,&len);
		addedge(x,y,len,c);
		s1=max(s1,c);
	}
	s1*=(n-1);
	
	spfa();
	s2++;
	for(int i=0;i<=s1;i++)
		if(f[T][i]!=1e8){
			if(sum(f[T][i]+1)==0) ans++;
			add(f[T][i]+1,1);
		}
	printf("%d
",ans);
	
	return 0;
}