好久不见,长假过后焕然一新的我回来了……
第一次学斜率优化是2年前…现在才写总结【微笑】
参考:论文《1D1D动态规划优化初步》
斜率优化是干啥的?
对动态规划的优化,将其 (O(n^2)) 的复杂度降为 (O(nlogn)) 或 (O(n))
第一次学还是初一,啥都不懂,只是觉得这种类似数形结合的方法真的很妙!
斜率优化模型
状态转移方程类似这样:
$ f[i]=mathop{min}limits_{j=1}^{i-1} lbrace a[i] imes x[j] + b[i] imes y[j]
brace $
我们可以把 (x[i]) 当成横坐标, (y[i]) 当成纵坐标,那么 ((x[i],y[i])) 可当做平面直角坐标系中一个点
$ f[i]=a[i] imes x[j] + b[i] imes y[j]$ 便表示平面内的一条直线,换个形式写为:
$ y[j]=-frac{a[i]}{b[i]} imes x[j] + frac{1}{b[i]} imes f[i]$
其中斜率 (-frac{a[i]}{b[i]}) 为定值,(f[i]) 前系数 (frac{1}{b[i]}) 为定值,对于不同的 (j) , (x[j],y[j]) 均已知
即对每个 (j) 可确定一条直线
要 (f[i]) 最小即要这条直线的纵截距最小
可以理解为一条斜率确定的线从下向上平移,碰到的第一个点为最优决策点 (j)
而一个重要的性质叫做:所有最优决策点都在平面点集的凸包上
(为什么大家都说显然啊…画图可直观理解,但证明大概要用线性规划知识…?orz)
然后可根据这个事实进行优化。
另一种理解方式
个人认为可更好想明白为啥在凸包上……
状态转移方程仍类似这样:
$ f[i]=mathop{min}limits_{j=1}^{i-1} lbrace a[i] imes x[j] + b[i] imes y[j]
brace $
我们考虑两个决策点 (j) 与 (k) ,若满足 (j>k) 且 (j) 优于 (k),则
移项可知 (-frac{a[i]}{b[i]}) 与 (frac{y[j]-y[k]}{x[j]-x[k]}) 的大小关系
(-frac{a[i]}{b[i]}) 是已知确定的,设其为 (kk)
同样把 ((x[i],y[i])) 看做平面直角坐标系中的点,(frac{y[j]-y[k]}{x[j]-x[k]}) 就为两点所在直线斜率
上述式子有两种情况:
情况一:(frac{y[j]-y[k]}{x[j]-x[k]} > kk)
翻译成文字:若这两点斜率大于 (kk) 则 (j) 优于 (k),反之亦然
那么所有的最优决策点不会出现如下图情况:
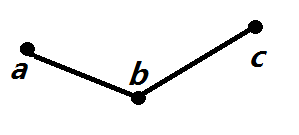
原因是:图中 (k_{ab}<k_{bc})
若 $ k_{ab} leq kk$,则 (a) 优于 (b) , (b) 不是最优决策点
若 (kk<k_{ab}<k_{ac}),则考虑 (bc) 段, (c) 优于 (b) , (b) 又不是最优决策点
所以最优决策点只能在一个斜率递减的凸包上。
情况二: (frac{y[j]-y[k]}{x[j]-x[k]} > kk)
与第一种情况类似,(略过长串过程),最优决策点只能在一个斜率递增的凸包上。
这就是一个很妙的性质啦!
应用分类
决策直线斜率与二元组坐标同时满足单调性
这应该是最经典最常见的应用了。
由于斜率变化单调,所以决策点在凸包上只会单调移动。
我们只需维护一个单调队列及决策指针,每次决策时移动指针至最优决策点,决策,然后将新状态插入队列中,删点维护凸壳。
复杂度 (O(n))
例题挺多啦,如 (bzoj1010) 玩具装箱,(bzoj1096) 仓库建设……
这里以 (bzoj3156) 防御准备 为例
题目:https://www.lydsy.com/JudgeOnline/problem.php?id=3156
令 (dp[i]) 表示在第 (i) 个检查点放置守卫塔且前 (i) 个检查点通过安全检查的最小花费
可列出状态转移方程:
令 (dp[i]+frac{1}{2}i^2 + frac{1}{2}i) 为 (x[i]),(i) 为 (y[i])
原方程可化为 $dp[i]==mathop{min}limits_{j=0}^{i-1} lbrace 1 imes x[j] - i imes y[j]
brace+a[i]+frac{1}{2}i^2-frac{1}{2}i $
最优决策点在斜率递减的凸包上
决策指针移动时不断删头,最优决策取队首
代码:
注意 (dp[0]) 的赋值以及 (long long)
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1000005;
typedef long long ll;
ll n;
ll q[N],h,t;
ll a[N],dp[N],g[N];
int main()
{
scanf("%d",&n);
for(ll i=1;i<=n;i++) scanf("%lld",&a[i]);
h=t=0;
dp[0]=g[0]=0;
q[t++]=0;
for(ll i=1;i<=n;i++){
while(t-h>1 && g[q[h+1]]-g[q[h]]<=i*(q[h+1]-q[h])) h++;
dp[i]=a[i]+1ll*i*(i-1)/2+g[q[h]]-i*q[h];
g[i]=dp[i]+i*(i+1)/2;
while(t-h>1 && (g[q[t-1]]-g[q[t-2]])*(i-q[t-1])>=(g[i]-g[q[t-1]])*(q[t-1]-q[t-2])) t--;
q[t++]=i;
}
printf("%lld
",dp[n]);
return 0;
}
其它情况
一种方法是用平衡树动态维护凸壳
另一种则是用 (CDQ) 分治。
复杂度 (O(nlogn))
例题如 (bzoj1492[NOI2007]) 货币兑换
题目:https://www.lydsy.com/JudgeOnline/problem.php?id=1492
题目真是复杂666
设 (dp[i]) 表示第 (i) 天可获得的最多的钱
状态转移方程:
需要维护斜率递减的凸包
代码:
先是 (splay) 版的
细节很多,要多多多注意
(eps) 要坑死我了。。。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
#define INF 1e12
#define eps 1e-9
using namespace std;
const int N = 100005;
typedef double db;
int n;
db s,A[N],B[N],R[N],dp[N];
struct node{
db x,y,lk,rk;
node *ch[2],*pa;
}pool[N],*root,*rf,*tmp;
int cnt;
db sl(node *p,node *q){
if(fabs(p->x-q->x)<eps) return INF;
return (p->y-q->y)/(p->x-q->x);
}
void rotate(node *p,int ty){
node *pa=p->pa,*son=p->ch[ty^1],*gp=pa->pa;
pa->ch[ty]=son; if(son) son->pa=pa;
p->ch[ty^1]=pa; pa->pa=p;
p->pa=gp; gp->ch[pa==gp->ch[1]]=p;
if(root==pa) root=p;
}
void splay(node *p,node *q){
while(p->pa!=q){
if(p->pa->pa==q)
rotate(p,p==p->pa->ch[1]);
else{
node *pa=p->pa,*gp=pa->pa;
int f=pa==gp->ch[0]; /**/
if(p==pa->ch[f]) rotate(p,f),rotate(p,!f);
else rotate(pa,!f),rotate(p,!f);
}
}
}
void insert(node *p,node *nd){
int f=(nd->x>p->x || fabs(nd->x-p->x)<eps);
if(!p->ch[f]){
p->ch[f]=nd;
nd->pa=p;
}
else insert(p->ch[f],nd);
}
node *findl(node *p,node *nd){ /**/
if(!p) return p;
db k=sl(p,nd);
node *q;
if(k<p->lk || fabs(k-p->lk)<eps){
q=findl(p->ch[1],nd);
return q ? q : p ;
}
else return findl(p->ch[0],nd);
}
node *findr(node *p,node *nd){
if(!p) return p;
db k=sl(p,nd);
node *q;
if(k>p->rk || fabs(k-p->rk)<eps){
q=findr(p->ch[0],nd);
return q ? q : p ;
}
else return findr(p->ch[1],nd);
}
void Ins(node *nd){
insert(root,nd);
splay(nd,rf);
node *p=findl(nd->ch[0],nd),*q=findr(nd->ch[1],nd);
if(p){
splay(p,root);
p->ch[1]=NULL;
nd->lk=p->rk=sl(p,nd);
}
else nd->lk=INF;
if(q){
splay(q,root);
q->ch[0]=NULL;
nd->rk=q->lk=sl(q,nd);
}
else nd->rk=-INF;
if(nd->lk < nd->rk) {// del nd
if(p && q) { splay(p,rf); splay(q,root); q->ch[0]=NULL; }
else if(p) { splay(p,rf); p->ch[1]=NULL; }
else if(q) { splay(q,rf); q->ch[0]=NULL; }
}
}
node *query(node *p,db k){
if(p->lk<k) return query(p->ch[0],k);
if(p->rk>k) return query(p->ch[1],k);
return p;
}
int main()
{
scanf("%d",&n); scanf("%lf",&s);
for(int i=1;i<=n;i++) scanf("%lf%lf%lf",&A[i],&B[i],&R[i]);
rf=&pool[++cnt];
for(int i=1;i<=n;i++){
if(i==1) dp[i]=s;
else{
tmp=query(root,-A[i]/B[i]);
dp[i]=max(dp[i-1],A[i]*tmp->x+B[i]*tmp->y);
}
tmp=&pool[++cnt];
tmp->y=dp[i]/(A[i]*R[i]+B[i]); tmp->x=tmp->y*R[i];
if(!root) {
root=tmp;
root->pa=rf; rf->ch[0]=root;
root->lk=INF; root->rk=-INF;
}
else Ins(tmp);
}
printf("%.3lf
",dp[n]);
return 0;
}
然后是 (CDQ) 分治
先上一篇 (CDQ) 大神论文,第一个例子就是这题:https://wenku.baidu.com/view/52f9c11cff00bed5b9f31d2d.html