洛谷P1772 [ZJOI2006]物流运输

题目描述

物流公司要把一批货物从码头A运到码头B。由于货物量比较大，需要n天才能运完。货物运输过程中一般要转停好几个码头。物流公司通常会设计一条固定的运输路线，以便对整个运输过程实施严格的管理和跟踪。由于各种因素的存在，有的时候某个码头会无法装卸货物。这时候就必须修改运输路线，让货物能够按时到达目的地。但是修改路线是—件十分麻烦的事情，会带来额外的成本。因此物流公司希望能够订一个n天的运输计划，使得总成本尽可能地小。

输入输出格式

输入格式：

第一行是四个整数n(l≤n≤100)、m(l≤m≤20)、K和e。n表示货物运输所需天数，m表示码头总数，K表示每次修改运输路线所需成本，e表示航线条数。接下来e行每行是一条航线描述，包括了三个整数，依次表示航线连接的两个码头编号以及航线长度(>0)。其中码头A编号为1，码头B编号为m。单位长度的运输费用为1。航线是双向的。再接下来一行是一个整数d，后面的d行每行是三个整数P(1<P<m)，a，b(1≤a≤b≤n)。表示编号为P的码头从第a天到第b天无法装卸货物（含头尾）。同一个码头有可能在多个时间段内不可用。但任何时间都存在至少一条从码头A到码头B的运输路线。

输出格式：

包括了一个整数表示最小的总成本。总成本=n天运输路线长度之和+K*改变运输路线的次数。

输入输出样例

输入样例#1： 

  5 5 10 8
  1 2 1
  1 3 3
  1 4 2
  2 3 2
  2 4 4
  3 4 1
  3 5 2
  4 5 2
  4
  2 2 3
  3 1 1
  3 3 3
  4 4 5

输出样例#1： 

32

说明

【样例输入说明】

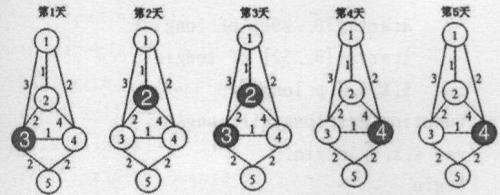
上图依次表示第1至第5天的情况，阴影表示不可用的码头。

【样例输出说明】

前三天走1-4-5，后两天走1-3-5，这样总成本为(2+2)*3+(3+2)*2+10=32。

_NOI导刊2010提高（01）

这道题的突破口可以说是m<=20吧

看到m这么小之后，我完美的想到了状压dp，复杂度n*(1<<m)*m……

（dp[i][st]表示第i天，路线为map[st]的最小成本）

本来以为可以过的，但是复杂度还是略微有些高，只对了3个点，其他都T了

QWQ

无奈之下只好又去翻题解，哎

同样是dp，dp[i]表示到第i天的最小成本，转移时枚举从j到i连续不改路线的最小成本

如何算从j到i连续不改路线时的路线长度是多少呢？

每次直接SPFA搞定（每次复杂度最最最多m*m*m）

这样就能过了啊！

代码：

（注意有的地方要转long long）

#include<cstdio>
#include<iostream>
#include<string.h>
#define INF 214748647
#define ll long long
using namespace std;

struct node{
    int v,len;
    node *next;       
}pool[2500],*h[25];
int cnt;
void addedge(int u,int v,int len){
    node *p=&pool[++cnt],*q=&pool[++cnt];
    p->v=v;p->next=h[u];h[u]=p;p->len=len;
    q->v=u;q->next=h[v];h[v]=q;q->len=len;     
}
int n,m;
int used[25][105];
ll f[105];

int d[25],s,t,vis[25],que[100005],mm[25];
int spfa(int l,int r){
    int u,v;
    memset(vis,0,sizeof(vis));
    memset(mm,0,sizeof(mm));
    for(int i=2;i<=m;i++) d[i]=INF;
    for(int i=1;i<=m;i++)
        for(int j=l;j<=r;j++) if(used[i][j]) mm[i]=1;
    d[1]=0;
    s=t=0;
    que[t++]=1;vis[1]=1;
    while(s<t){
        u=que[s++];
        vis[u]=0;
        for(node *p=h[u];p;p=p->next){
            v=p->v;
            if(d[v]>d[u]+p->len && mm[v]==0){
                d[v]=d[u]+p->len;
                if(!vis[v]) que[t++]=v,vis[v]=1;                   
            }
        }
    }
    return d[m];
}

int main()
{
    int K,E,D,i,j,x,y,z;
    scanf("%d%d%d%d",&n,&m,&K,&E);
    for(i=0;i<E;i++)
        scanf("%d%d%d",&x,&y,&z),addedge(x,y,z);
    scanf("%d",&D);
    for(i=0;i<D;i++){
        scanf("%d%d%d",&x,&y,&z);
        for(j=y;j<=z;j++) used[x][j]=1;
    }
    
    for(i=1;i<=n;i++){
        f[i]=(ll)spfa(1,i)*i;
        for(j=2;j<=i;j++){
            f[i]=min(f[i],f[j-1]+(ll)spfa(j,i)*(i-j+1)+K);                  
        }
    }
    printf("%lld",f[n]);

    return 0;    
}