题目描述
印尼首都雅加达市有 N 座摩天楼,它们排列成一条直线,我们从左到右依次将它们编号为 0 到 N − 1。除了这 NN 座摩天楼外,雅加达市没有其他摩天楼。
有 M 只叫做 “doge” 的神秘生物在雅加达市居住,它们的编号依次是 0 到 M − 1。编号为 i 的 doge 最初居住于编号为 Bi 的摩天楼。每只 doge 都有一种神秘的力量,使它们能够在摩天楼之间跳跃,编号为 i 的 doge 的跳跃能力为 Pi (Pi>0)。
在一次跳跃中,位于摩天楼 b 而跳跃能力为 p 的 doge 可以跳跃到编号为 b − p (如果 b − p < N)或 b+p(如果0≤b+p<N)的摩天楼。
编号为 0 的 doge 是所有 doge 的首领,它有一条紧急的消息要尽快传送给编
号为 1 的 doge。任何一个收到消息的 doge 有以下两个选择:
跳跃到其他摩天楼上;
将消息传递给它当前所在的摩天楼上的其他 doge。
请帮助 doge 们计算将消息从 0 号 doge 传递到 1 号 doge 所需要的最少总跳跃步数,或者告诉它们消息永远不可能传递到 1 号 doge。
输入输出格式
输入格式:
输入的第一行包含两个整数 N 和 M。
接下来 M 行,每行包含两个整数 Bi 和 Pi。
输出格式:
输出一行,表示所需要的最少步数。如果消息永远无法传递到 1 号 doge,输出 −1。
输入输出样例
5 3 0 2 1 1 4 1
5
说明
【样例解释】
下面是一种步数为 5 的解决方案:
0 号 doge 跳跃到 2 号摩天楼,再跳跃到 4 号摩天楼(2 步)。
0 号 doge 将消息传递给 2 号 doge。
2 号 doge 跳跃到 3 号摩天楼,接着跳跃到 2 号摩天楼,再跳跃到 1 号摩天楼(3 步)。
2 号 doge 将消息传递给 1 号 doge。
【数据范围】
所有数据都保证 0≤Bi<N。
子任务 1 (10 分)1≤N≤10
1≤Pi≤10
2≤M≤3
子任务 2 (12 分)1≤N≤100
1≤Pi≤100
2≤M≤2000
子任务 3 (14 分)1≤N≤2000
1≤P≤2000
2≤M≤2000
子任务 4 (21 分)1≤N≤2000
1≤Pi≤2000
2≤M≤30000
子任务 5 (43 分)1≤N≤30000
1≤Pi≤30000
2≤M≤30000
题解:
哇哇哇这道题A掉真不容易
这道题看到就想着建图,但是直接建肯定是不行的。
为啥不行呢?原来,对于某一个doge的p值,我们的建图方法是这样滴:
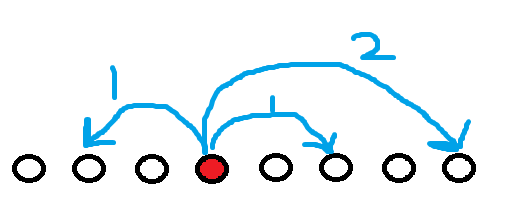
如果p值较大的话,那还好办,因为不会连出去多少边
但是,如果p值小的话,那么每一个点可能会往外连好多个边,而且可能有重复的!
复杂度可能接近 n² 哦
那么,如何改进建边方法?
老师教我们做分层图(似乎也叫分块?并不太清楚……)
对于p值较大的,比如大于sqrt(n)的,我们还直接建边
但是对于p值较小的,我们就对于不同的p值分别建图,然后每两个可一步到达的“相邻”点间都连正反两条边
就像这样:
p=1层的图:
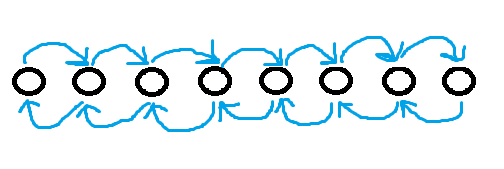
p=2层的图:
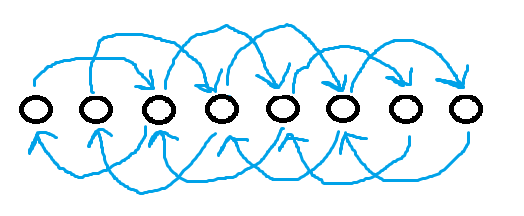
(画图好累……)
好了大概层里建图就是这样
可是不能光在一个层里面跑啊,得在不同层间跑
那么不同层间的边怎么连?
不同层间的边其实就相当于一栋楼中有些可跳距离不同的doge,那对于每一个doge都把同一个点不同层的点指向该点(这样说好抽象啊……看代码应该好理解些)
这样建图复杂度是nlogn的
这样图建完后跑最短路就可以了
我一开始用dijkstra堆优化,但是始终T一个点。后来改成SPFA又修改了许多耗时的地方才A掉……95分了好长时间……
我做这道题时中间有一段时间一直65分,因为我在建图时有一块儿想错了
我把p值较大的暴力建图时是按照p值较小的建图方法建的(如上2图)
但是这样是有问题的

两者的区别不单是前者边少后者边多,更是前者只能从一个点出发去其他点,而后者可从每一个点出发去其他点!
虽然感觉上求两点之间距离这两种方法是一样的,但当有其他点、边或其他操作插进来后就很不一样了
比如前一个图,第三个点与第四个点是无法互相到达的,而在后面图中就可以
下次写题是一定要注意这一点!要想清楚了!
代码:

1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<math.h> 5 #include<queue> 6 #define INF 1000000007 7 using namespace std; 8 9 const int MAXN = 30005; 10 struct node{ 11 int v,len,lev; 12 node *next; 13 }pool[500*MAXN],*h[400][MAXN]; 14 int cnt; 15 16 int read(){ 17 int x=0,f=1; 18 char ch=getchar(); 19 while(ch>'9' || ch<'0') ch=getchar(); 20 while('0'<=ch && ch<='9') x=x*10+ch-'0',ch=getchar(); 21 return x; 22 } 23 24 void addedge(int u,int lu,int v,int lv,int len){ 25 node *p=&pool[++cnt]; 26 p->v=v;p->len=len;p->lev=lv; 27 p->next=h[lu][u];h[lu][u]=p; 28 } 29 30 int n,m,sn; 31 int b[MAXN],p[MAXN],vis[405]; 32 33 int d[400][MAXN],use[400][MAXN]; 34 struct qqq{ 35 int num,lev; 36 }; 37 queue<qqq> que1; 38 void spfa(int S,int lS,int T){ 39 int u,v,l; 40 qqq newq,now; 41 for(int i=0;i<sn;i++) 42 for(int j=0;j<n;j++) d[i][j]=INF; 43 while(!que1.empty()) que1.pop(); 44 d[lS][S]=0; 45 newq.num=S;newq.lev=lS; 46 que1.push(newq); 47 while(!que1.empty()){ 48 now=que1.front();que1.pop(); 49 u=now.num;l=now.lev; 50 for(node *p=h[l][u];p;p=p->next) 51 { 52 v=p->v; 53 if(d[p->lev][v]>d[l][u]+p->len){ 54 d[p->lev][v]=d[l][u]+p->len; 55 if(use[p->lev][v]) continue; 56 newq.num=v;newq.lev=p->lev; 57 que1.push(newq); 58 use[p->lev][v]=1; 59 } 60 } 61 use[l][u]=0; 62 } 63 } 64 65 int main() 66 { 67 int i,j,l2,S,T,lS; 68 n=read();m=read(); 69 for(i=0;i<m;i++) b[i]=read(),p[i]=read(); 70 sn=min((int)sqrt(n),100); 71 S=b[0];T=b[1]; 72 if(p[0]<sn) lS=p[0];else lS=0; 73 74 //addedge 75 for(i=0;i<m;i++){ 76 if(p[i]>=sn){ 77 vis[0]=1; 78 for(j=b[i]%p[i];j<n;j+=p[i]){ 79 if(j==b[i]) continue; 80 addedge(b[i],0,j,0,abs(j-b[i])/p[i]); 81 } 82 } 83 else vis[p[i]]=1; 84 } 85 for(i=1;i<sn;i++) 86 if(vis[i]){ 87 for(j=0;j+i<n;j++){ 88 addedge(j,i,j+i,i,1); 89 addedge(j+i,i,j,i,1); 90 } 91 } 92 //level 93 for(i=0;i<m;i++){ 94 if(p[i]<sn) l2=p[i]; 95 else l2=0; 96 for(j=0;j<sn;j++) 97 if(j!=l2 && vis[j]){ 98 addedge(b[i],j,b[i],l2,0); 99 } 100 } 101 102 //spfa 103 spfa(S,lS,T); 104 int ans=INF; 105 for(i=0;i<sn;i++) ans=min(ans,d[i][T]); 106 if(ans==INF) printf("-1 "); 107 else printf("%d ",ans); 108 109 return 0; 110 }
