聚类是根据样本的相似度,将样本归并到一类别的方法。
聚类相似度的确定则需要根据样本的特性选择合适的相似度度量方法来计算。一般相似度的度量方法有距离度量,即将样本看作向量空间的集合,以样本在空间中的距离表示样本之间的相似度,而常见的距离度量有欧氏距离。
相似度的度量方法还有:相关系数,夹角余弦等等的方法。
在确定相似度的度量方法后,聚类的算法也有两种:
层次聚类(自下而上型):
层次聚类在初始时,将每个样本各自分为一类,将距离最近的两个类合并,成为一个新的类别,重复直到其满足停止条件。
层次聚类算法(采用欧氏距离):
输入:n个样本组成的样本集合及样本之间的距离;
输出:对样本集合的一个层次化聚类。
(1)计算n个样本两两之间的距离,放入矩阵D,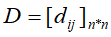
(2)构造n个类,每个类只包含一个样本;
(3)合并类间距离最小的两个类成为一个新的类;
(4)计算新类与其他类的距离,若类的个数达到预定的个数,则停止,否则重复步骤(3)
对于上述的层次聚类的算法,其复杂度为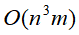 (m为样本的维数),以为着其复杂度随样本规模n呈立方增长。
(m为样本的维数),以为着其复杂度随样本规模n呈立方增长。
k均值聚类:
k均值聚类则是基于中心聚类的方法,通过迭代将样本分到k个类中,使样本与其所属类的中心或均值最近。
理论上,为计算样本整体的聚合程度能定义一个样本与其所属类的中心之间的距离的总和函数,即样本整体的聚合程度的损失函数:
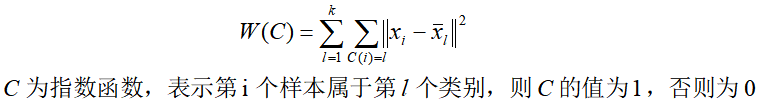
而求解样本整体最优的聚合划分即转化为求能使上述的损失函数达到最小的最优聚类划分
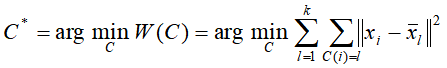
同样,若按该损失函数去优化最优聚合划分,此问题的复杂度也将是指数级的复杂度。
不过k均值聚合算法通过迭代的方式能使问题的复杂度降为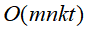 (m为样本的维数,k是为样本设定的类别个数,t为迭代次数),故能用k均值聚合算法求损失函数逐步减小的聚类划分方法。
(m为样本的维数,k是为样本设定的类别个数,t为迭代次数),故能用k均值聚合算法求损失函数逐步减小的聚类划分方法。
k均值聚类算法(采用欧氏距离):
输入:n个样本组成的样本集合;
输出:样本的集合的聚类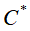
(1)为样本随机选择k个样本点作为聚类的中心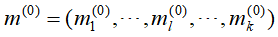
(2)进行第 t 次迭代,计算每个样本到各个类中心的距离,选择与类中心距离最近的,将该样本划归到那个类,构成聚类结果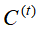
(3)对(2)中的结果,计算各个类的样本均值,并更新作为新的类中心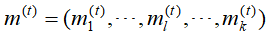
(4)如果迭代收敛或者达到停止条件,输出样本的最终聚类结果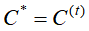 ,否则,返回(2)进行下一轮迭代。
,否则,返回(2)进行下一轮迭代。
# 随机选择 k 个样本初始化为类别中心 self.__gen_center(X_train,k) self.dist = np.zeros((n_sample, self.k_clusters)) cent_pre = np.zeros(self.cluster_centers_.shape)
# 样本类别中心的变化 cent_move = np.linalg.norm(self.cluster_centers_ - cent_pre) epoch = 0 # 迭代次数 from copy import deepcopy while epoch < self.max_iter and cent_move > self.tol: epoch += 1 # 首先计算每个样本离每个类中心的距离 for i in range(self.k_clusters): self.dist[:,i]=np.linalg.norm(X_train-self.cluster_centers_[i], axis=1) # 选择与类中心距离最近的,将该样本划归到那个类 self.labels_ = np.argmin(self.dist, axis=1) cent_pre = deepcopy(self.cluster_centers_) # 计算每个类别下的均值坐标,更新类别中心 for i in range(self.k_clusters): self.cluster_centers_[i] = np.mean(X_train[self.labels_ == i], axis=0) cent_move = np.linalg.norm(self.cluster_centers_ - cent_pre) |
k均值聚类的部分代码实现
虽然,k均值聚类算法能降低聚类的复杂度,但这种方法不能保证得到能使损失函数达到全局最小的最优聚类划分,而且为样本设定的类别的初始中心会影响聚类的结果。