朴素贝叶斯(Naive Bayes)是基于贝叶斯定理与特征条件独立假设的分类方法。即对于给定的训练数据,首先基于特征条件独立假设学习输入输出联合概率分布,然后基于此模型,对给定输入的x,利用贝叶斯定理输出最大的后验概率y。
假设输入空间X,对应的输出空间Y为标记集合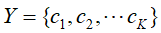 ,而且在这些数据集中先验分布概率为:
,而且在这些数据集中先验分布概率为: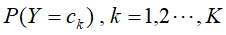 ,条件分布概率为:
,条件分布概率为: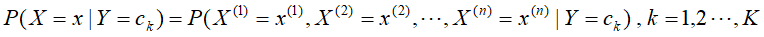 。
。
然而,对于条件分布概率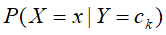 ,其每个
,其每个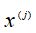 有
有 种取值,且输出空间Y的标记也有K种取值,那么条件分布概率的计算将有指数个参数需要参与。如此庞大的参数规模可能致使条件分布概率变为不可能。
种取值,且输出空间Y的标记也有K种取值,那么条件分布概率的计算将有指数个参数需要参与。如此庞大的参数规模可能致使条件分布概率变为不可能。
对此,朴素贝叶斯法对条件分布概率做了条件独立性的假设,使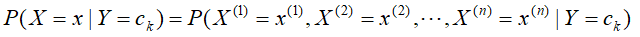 变为
变为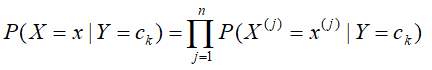 ,让条件概率计算的参数分布到各个独立性条件概率的计算上。
,让条件概率计算的参数分布到各个独立性条件概率的计算上。
接着对应的输入X=x的输出标记分类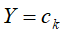 ,可由计算后验概率,得到的输入X=x和输出标记分类
,可由计算后验概率,得到的输入X=x和输出标记分类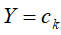 最大的后验概率
最大的后验概率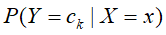 可判断,输入x的对应标记分类类别。后验概率的计算根据利用朴素贝叶斯法的贝叶斯定理进行:
可判断,输入x的对应标记分类类别。后验概率的计算根据利用朴素贝叶斯法的贝叶斯定理进行:
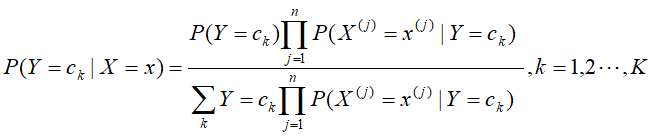
在上述的计算公式中,由于分母是相同的,故可以对公式做进一步的简化:
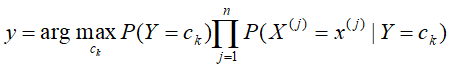
算法流程:
输入:训练数据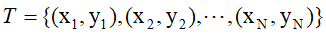 ,其中
,其中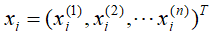 ,
,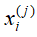 是第i个样本的第j个特征,
是第i个样本的第j个特征,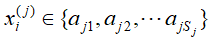 ,
,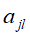 是第j个特征可能取的第
是第j个特征可能取的第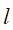 个值,
个值, ;实例x;
;实例x;
(计算的过程中,用极大似然估计可能会出所要估计的概率为0的情况,而这会影响到后验概率的计算结果,使的实例x的分类结果产生偏差。为了消除差,采用贝叶斯估计)
输出:实例x的分类
- 如果有先验概率,直接输入;没有则根据贝叶斯估计计算先验概率:
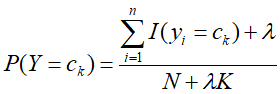
- 同样利用贝叶斯估计分别计算第k个分类条件下,第j个特征可能取第
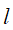 个值的条件概率:
个值的条件概率:
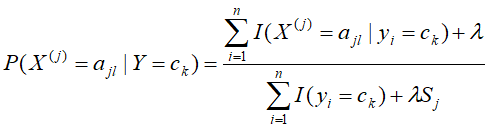
- 对实例x分别计算:
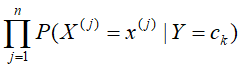
然后选取其中计算结果最大的一个便能判别实例x对应y的分类类别。
朴素贝叶斯的主要优点有:
1)朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
2)对小规模的数据表现很好,能个处理多分类任务,适合增量式训练,尤其是数据量超出内存时,我们可以一批批的去增量训练。
3)对缺失数据不太敏感,算法也比较简单,常用于文本分类。
主要缺点有:
1) 理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
2)需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
3)由于我们是通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率。
4)对输入数据的表达形式很敏感。