一.自顶向下伸展树
伸展树考虑到局部性原理,为使整个查找时间更小,将被频繁查找的节点调整到根部,即通过不断改变树的结构,从而使其的操作保持了O(logN)的摊还时间界。
伸展树的单旋转、一字形旋转和之字形旋转的旋转示意图如下,

图1-1 伸展树的单旋转、一字形旋转和之字形旋转的展开旋转示意图
在执行完最后一步的展开后,需要对L、R以及中间树进行合并,形成单一的树,合并的示意图如下
图1-2 伸展树执行完伸展后的合并
伸展树的自顶向下的展开代码如下,
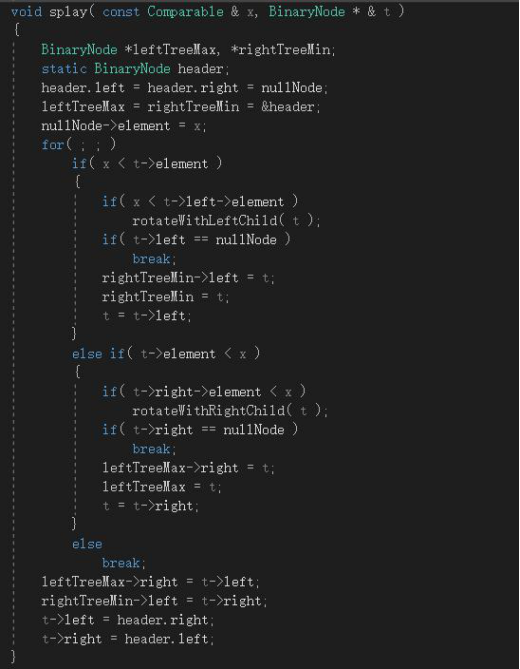
图1-3 伸展树自顶向下的展开代码
伸展树将最近搜索的节点放在最容易搜索的根节点的位置,让其在许多环境中得到应用,比如网络应用中,某些固定内容会被大量重复访问。伸展树可以让这种重复搜索以很高的效率完成。
二.红黑树
红黑树是一种自平衡二叉查找树,和AVL树类似,都是在进行插入和删除操作时通过特定操作使树保持平衡,从而获得较高的查找性能。
红黑树的特性:
(1) 每个节点或者是黑色,或者是红色。
(2) 根节点是黑色。
(4) 如果一个节点是红色的,则它的子节点必须是黑色的。
(5) 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
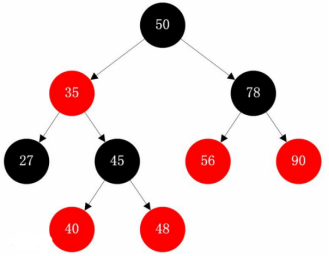
图2-1 常规的红黑树
在红黑树上查找操作不需要对其修改,但在插入和删除操作中,红黑树的性质可能遭到破坏,需要恢复红黑属性,不过其插入和删除的操作的时间复杂度仍为O(log n),但是这些操作却有些复杂。
红黑树的插入和删除可以与伸展树以自顶向下的方式进行。
设当前节点为Current,其兄弟节点为Brother,父节点为Parent,祖父节点为Grand,曾祖父为Great(空节点的默认颜色是黑色)。
在自顶向下的插入过程中,若Current节点有两个红孩子时,进行颜色翻转(使Current为红,其两孩子为黑,不管Current是否为根,都令根为黑)。
颜色翻转后,若Current的父节点Parent为红,则进行旋转。
自顶向下的插入操作实现代码如下,


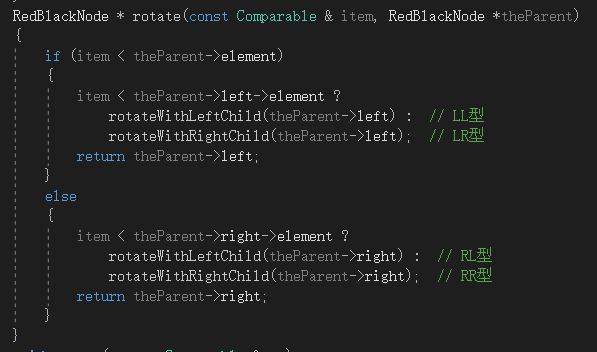
图2-2 红黑树自顶向下的插入过程
在自顶向下的删除过程中,与AVL树同样将删除非叶子节点转换为删除叶子节点,具体过程如下
第一步,检查根,并将根变为红色,
1. 若根有两个黑儿子,向下并进入第二步
2. 其他则进入第二步B情况
第二步,
A情况,当前节点Current有两个黑儿子
A1.兄弟节点Brother节点也有两个黑儿子,翻转Current、Parent和Brother节点的颜色,向下(示意图如下)
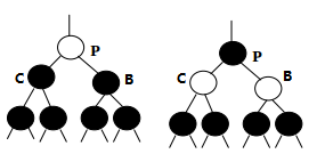
图2-3 红黑树自顶向下删除A1的情况
A2.兄弟节点Brother节点的左儿子为红,进行之字形旋转,并翻转Current和Parent颜色,向下(示意图如下)

图2-4 红黑树自顶向下删除A2的情况
A3.兄弟节点Brother节点的右儿子为红,进行一字形旋转,并翻转Current、Parent、Brother和Brother右儿子节点的颜色,再向下(示意图如下)
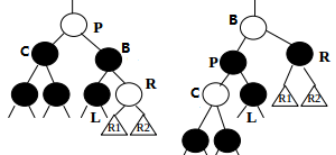
图2-5 红黑树自顶向下删除A3的情况
B情况,当前节点Current至少有一个红儿子,
Current节点继续向下,若新的Current节点为红,继续向下。若新的Current节点为黑,则单旋转Brother节点和Parent节点,同时翻转Brother和Parent节点,回到第二步;
第三步,最终找到要删除节点,这是一个叶节点,将节点以红节点身份删除,否则转换为删除叶子节点;
第四步,将根恢复为黑色。