算法设计常见的5种基本技巧,有贪婪算法、分治算法、动态规划、随机化算法和回溯算法。
一.贪婪算法
虽然每次的选择都是局部最优,当在算法结束的时候,其期望是全局最优才是正确的。不过有时,在不同条件与要求下时,最优解的答案可能不止有一个或不一样,而贪婪算法也可以得出一个近似的答案。
1.多处理器作业调度
在多处理器的调度完成作业的问题中,表1-1中的作业可也按图1-1和图1-2的方式进行调度的到平均时间最小的最优答案。
|
作业 |
J1 |
J2 |
J3 |
J4 |
J5 |
J6 |
J7 |
J8 |
J9 |
|
时间 |
3 |
5 |
6 |
10 |
11 |
14 |
15 |
18 |
20 |
表1-1 作业与时间表
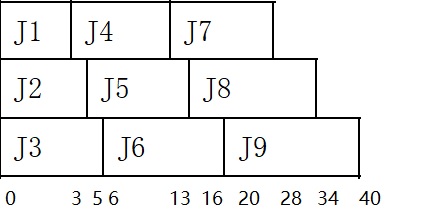
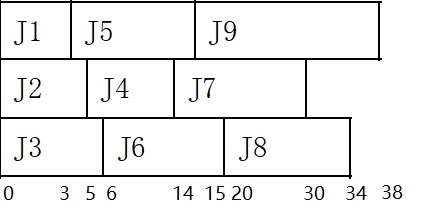
图1-1 作业调度方式1 图1-2 作业调度方式2
在这两种不同的作业调度方式中,第一种调度方式使用贪婪算法,每个处理器开始按序首先调度处理作业时间要求最少的先进行处理,得到平均处理时间为18.33。第二种调度方式中,不改变作业调度的相对顺序,而改变其在其他处理器中进行处理,得出的平均处理时间同样为18.33。
然而,在第二种调度方式中,作业的最后完成时间为38,而第一种的最后完成时间为40。如果在考虑作业的最后完成时间的情况下,第一种调度方式所使用的贪婪算法则不算是得到最优的答案。
贪婪算法的另一项应用就时装箱问题,运用贪婪算法,装箱问题可以得到较快的解决速度,而得到的答案未必最优,但却也近似最优。
2.哈夫曼算法
哈夫曼算法也是一种典型的运用贪婪算法的算法。
在森林中,选取两棵权值最小的数形成新的树,再在其中选取两棵权值最小的数形成新的树,直到森林中最后只剩一棵树,即为权值最小的树。哈夫曼的代码实现如下,
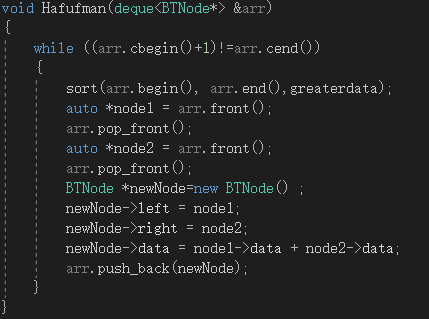
图1-3 哈夫曼树算法代码实现
若用优先队列实现哈夫曼算法,可将其运行时间优化为O(NlogN)。
二.分治算法
分治算法不是简单的递归,而是将大的问题递归解决较小的问题,然后从子问题的解构建原问题的解。比如,快速排序和归并排序算分分治算法,而图的递归深度搜索和二叉树的递归遍历则不是分治算法的运用。
分治算法运行时间的计算有一重要定理
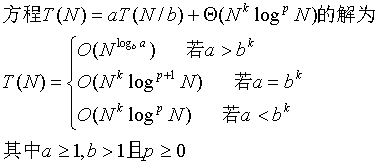
分治算法有较广泛的运用,很多规模较大的问题都可以用分治算法分解成独立的小问题解决。
快速选择算法是基于快速比较的一种分治算法的运用。对于规模较大的选择问题,在快速选择算法中用五元中值组取中值分割法使递归的子问题最多为原问题的规模的70%,以加快算法的效率,使运行时间为O(N)。
五元中值组取中值分割法即将N个元素分成每5个元素一组,运用8次比较找出每组的中值,得到约(N/5)个中值组,再对中值组调用分割的快速选择算法,直至找到第k小的元素。
在位数较多的整数相乘中,使用分治算法对其的运算进行优化,可将其运行时间优化为亚二次方时间。同样,在繁琐的矩阵乘法中,分治算法可将其运行时间优化为亚立方时间。
三.动态规划
动态规划与分治算法的区别是,两种算法同样是将较大的问题分解成较小问题,而动态规划对这些较小的问题并不是对原问题明晰的分割,其中一部分是被重复求解的,因此动态规划将较小问题的解记录下来,使得在处理较大问题的时候,可以不用重复去处理较小的问题,而是直接利用所记录的较小问题的答案来求解。
动态规划的典型运用就是对斐波那契数T(N)=T(N-1)+T(N-2)的求解,斐波那契数的求解同样可以运用分治算法,不过在其使分治算法中,其运行时间是随着N呈指数增长的,这显然会造成程序效率的低效。
而对斐波那契数使用动态规划求解的时候,计算T(N)只需将前面求解过的T(N-1)和T(N-2)进行相加即可,这种算法的实现也比较简单,代码可以实现如下,

图3-1 使用动态规划设计的斐波那契数求解算法代码
Floyd算法在求图的每一个顶点到其他所有顶点的最短路径中也应用了动态规划的设计技巧。虽然dijkstra算法通过迭代V次也可以以O(V^3)求出,但Floyd算法在求解稠密图的时候更快,且能应对存在负边值无圈的图。
该算法在求解顶点i和j之间的最短路径时,尝试绕过其他顶点k来求最短路径,并保留相应的结果,以备其他顶点在求解时使用,其代码的实现也相对容易,设置两个矩阵以保留最短路径权值和路径通路,实现如下

图3-2 Floyd算法的实现
四.随机化算法
随机化算法的一个应用是在快速排序中对枢纽元素的选择,使得算法的运行时间不止依赖于特定的输入,还而且还依赖于所出现的随机数。虽然一个随机化算法的最坏情形运行时间常常与非随机化算法的最坏情形运行时间相同,但两者还是有区别的,好的随机化算法没有坏的输入,而只有坏的随机数。
即在非随机化算法中,存在特定的输入序列总使得算法产生最坏的O(N^2)运行时间。如果运用随机化算法,且将该特定的序列输入运行,该算法的每一次运行将会得到不同的运行时间。
随机化算法的第二个应用是测试大数是否为素数,虽然该算法会出错,但随着测试次数的增多,那么错误的概率可以小到忽略不计。
五.回溯算法
回溯算法相当于穷举搜索的巧妙实现,对比蛮力的穷举搜索,回溯算法可以对一些不符合要求的或者是重复的情况进行裁剪,不再对其进行搜索,以减少搜索的工作量提高效率。比如,在图运用回溯算法的深度优先搜索遍历中,会对已搜索遍历过的顶点进行标记,避免下次的回溯搜索中对再次出现的该顶点进行重复遍历。
书中一例子是收费公路重建问题的应用。
对距离集合D,在一条路径上重构出符合距离集合D的点集X。比如,对距离集合D={1,2,2,2,3,3,3,4,5,5,5,6,7,8,10}重构出点集X,而重建所的到的决策树如下图5-1,对于下x4=7的决策点,其下的决策都的得不到符合距离集合D的要求结果,因此需要回溯到x5=8的决策点,再对其下同下x4=7对等的决策点x2=3进行测试,以求最终结果。
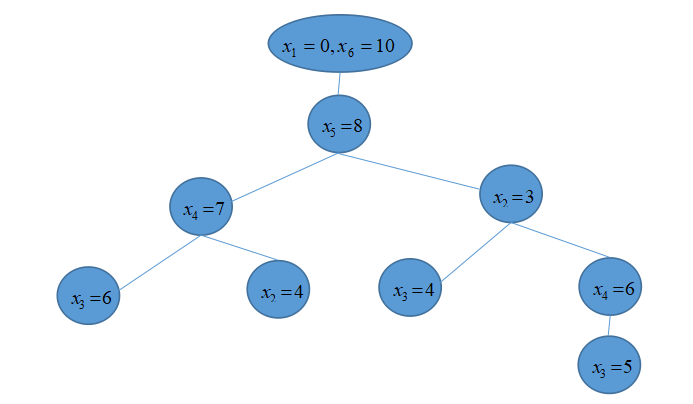
图5-1 收费公路重建距离集D对应的决策树
重建完后,可以得到如下结果,

图5-2 距离集合D对应的点集重建