树和二叉树

6.1 树的定义与基本术语

树：是n（n>=0）个结点的有限集合T。

       n=0时（没有结点），称为空树。

        n>0时， 必有一根；其余n-1个结点可以划分为m个根的子树。

每棵树除了根结点以外，每个结点有且仅有一个直接前驱，但可以有0个或多个直接后继。

基本概念及常用术语

1. 结点的度：一个结点的子树个数。

2. 树的度：树中，结点的度的最大值。

3. 叶结点（终端结点）：度为0的结点，即无后继的结点。

4. 分支结点（非终端结点）：度不为0的结点。

5. 结点的层次：从根结点开始定义，根结点的层次为1，根结点的直接后继层次为2，依次类推。

6. 树的高度（深度）：树中所有结点层次的最大值。

7. 孩子结点：结点的直接后继都称为该结点的孩子结点。

8. 父结点：若D是B的直接后继，那么就称B是D的双亲结点

9. 兄弟结点：几个结点的父结点是同一个，那么这几个结点就称为兄弟结点。

6.2 二叉树

二叉树的定义：

在二叉树中，每个结点至多有2个儿子，并且有左、右之分，分别称作左孩子、右孩子。

二叉树中，即使是一个儿子也有左右之分。

二叉树的性质：

【性质1】 若二叉树的层次从 1 开始计数，则在二叉树的第 i 层最多有 2 ^{i - 1} 个结点。（i >=1）

                  若层次从 0 开始，第 i 层最多有 2 ⁱ 个结点。

【性质2】  高度为 k 的二叉树最多有 2 ^k -1 个结点。

                   高度为 k 的二叉树最少有 k 个结点。

【性质3】  具有 n（n>=1）个结点的二叉树的高度最多为 n。

                   具有 n（n>=1）个结点的二叉树的高度最少为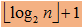 

【性质4】 对任何一颗二叉树，如果其叶结点有 n₀ 个，度为2的结点有 n₂个，则有  n₀ = n₂ + 1

【性质5】 n个结点可以组成多少种不同构的二叉树？

                               

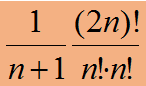
满二叉树： 一颗高度为 h 且有 2 ^h -1 个结点的二叉树。

完全二叉树：

                 若将满二叉树最后一层的结点，从右向左连续缺若干结点，就是完全二叉树。

在完全二叉树（满二叉树）中，若某个结点没有左二子，则它一定没有右儿子，即该结点是一个叶结点。

【性质6】 具有 n（n>=1）个结点的完全二叉树的高度为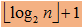 

【性质7】  如果完全二叉树各层次结点从1开始编号：1,2,3，...，n， 则有以下关系：

1. 仅当 i =1 时，结点 i 为根结点

2. 当 i >1 时，结点 i 的父结点为 i / 2

3. 结点 i 的左儿子结点为 2 * i

4. 结点 i 的右儿子结点为 2 * i + 1

5. 若 2 * i >n，则结点 i 无左二子

6. 若 2 * i +1 >n，则结点 i 无右儿子

二叉树的存储结构

二叉树的顺序存储结构

将 结点编号 与 数组下标 进行对应，然后将二叉树中结点存储的数据元素存储在一维数组对应的位置中。

联系【性质7】体现树中结点间的父子关系。

A	B	C	D	E	F	G	H	I	J	K	L
1	2	3	4	5	6	7	8	9	10	11	12

如表，若要找第9个结点的父结点，那么就是 9/2 取整等于 4，所以 I 的父结点就是 D。

          若要找第4个结点的左儿子结点，那么就是 2*4=8，所以 D 的左儿子结点就是 H。

二叉树的链式存储结构

leftChild

data

rightChild

若二叉树含有 n 个结点，则它的二叉链表中必含有2n个指针域，其中必有n+1个是空的链域。

空树：  root == NULL

二叉树结点及二叉树的定义：

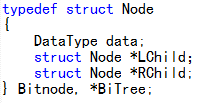
 建树代码：