一、 文献阅读
1.《基于OpenMP的分子动力学并行算法的性能分析与优化》时间:201201[ll1]
分析Critical方法的并行性能,提出优化的三角形方法,所提方法中每个线程所计算的粒子数固定,且粒子数目呈阶梯状上升,使得各线程能够错时到达临界区,从而使程序在临界区的闲置时间比Critical方法减半,加速比明显提高。
(1) MD串行算法
基于截断半径采用两种不同的算法来加速模拟:
近邻列表法[ll2] :通过建立列表保存每个粒子周围截断半径Rc区域内的相邻粒子,根据列表计算作用在这个粒子上的力。(可计算一个粒子所受力时避免搜索整个模拟空间)
元胞法[ll3] :将模拟体系分割成许多元胞,元胞边长d等于或略大于截断半径Rc,进行作用力计算时只需在周围26个元胞和当前元胞中查找相邻粒子。
两种方法结合使用,采用近邻表法计算作用力,构建近邻表时采用元胞法搜索可能的近邻粒子,从而降低近邻表构建任务的时间复杂度。
(2) 基于OpenMP的MD并行算法
在代码设置critial section(临界区)[ll4] 的方法,实现无数据竞争的牛顿第三定律策略(Critical方法)。
临界区的存在导致并行程序受到较大的影响。每个线程在临界区内做的工作都是相同的:将f_local()数组加到f()数组里。
图 ( a) 演示的线程数 Nth 为 8,可以分析出此时并行程序的闲置时间。从图中看出每个线程都要在临界区闲置 7个Tc,则总的闲置时间是56Tc。推广到一般情况下,可得总闲置时间为 Nth ( Nth - 1) Tc,其中在临界区前的闲置时间为 Nth ( Nth - 1) Tc /2。文中只提线程数 Nth,默认线程数等同于计算核心数。

(3) 优化方法
Critical方法的重要特点是临界区内只有一个线程在进行计算,其他进入过和未进入过临界区的线程都在闲置状态。如果能让未进入过临界区的线程不必再临界区等待而继续执行力计算的任务,则可避免临界区前的等待。
在临界区前的闲置时间为Nth(Nth-1)Tc/2,新方法(三角形法[ll5] )可以让闲置时间减少为原来的一半。图b为改进方法的时间线。由图 ( b) 可以看出该方法可以减少线程在临界区的闲置时间,以线程数 Nth = 8为例: 线程1要闲置 7Tc,线程2 要闲置6Tc,线程3 要闲置5Tc,……,总的闲置的时间由原来的 56Tc 减少到 28Tc,时间节省了一半。
(4) 结果对比
16个计算核心的SMP服务器上进行测试。
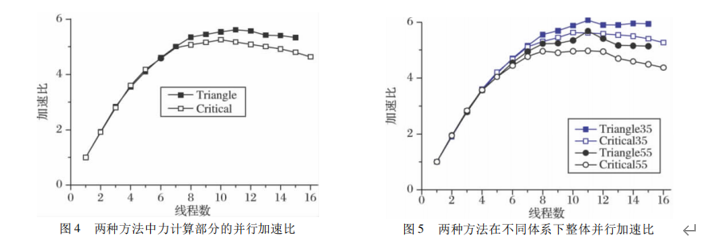
从图 4 看出,当线程数大于 7 时,三角形方法的力计算部分加速比明显高于Critical 方法,与前面的分析相符。在线程数为 11 时,两种方法加速比分别为 5.17 和 5.61,三角形方法比 Critical方法提高了约 9个百分点。如图 5 所示,35 和 55 代表两种不同大小的体系。可以看出随着线程数增大,相同体系下三角形方法始终要比Critical 方法更好,当然较大体系的加速比会比较小体系的略低。
二、 带宽速度
|
GPU:显卡型号 Tesla K80 |
||
|
Host to Device Bandwidth 1 Device(s) |
Transfer Size (Bytes):33554432 |
Bandwidth(MB/s):7443.8 |
|
Device to Host Bandwidth 1 Device(s) |
Transfer Size (Bytes):33554432 |
Bandwidth(MB/s): 8784.2 |
|
Device to Device Bandwidth 1 Device(s) |
Transfer Size (Bytes):33554432 |
Bandwidth(MB/s): 152045.6 |
三、 CUDA C学习
并行归约的优化:
并行归约问题:在向量中执行满足交换律和结合律的运算,为归约问题。
If((tid % (2 * stride) ) == 0,只对偶数ID 的线程为true,这会导致很高的线程束分化。
1. 改善并行规约的分化
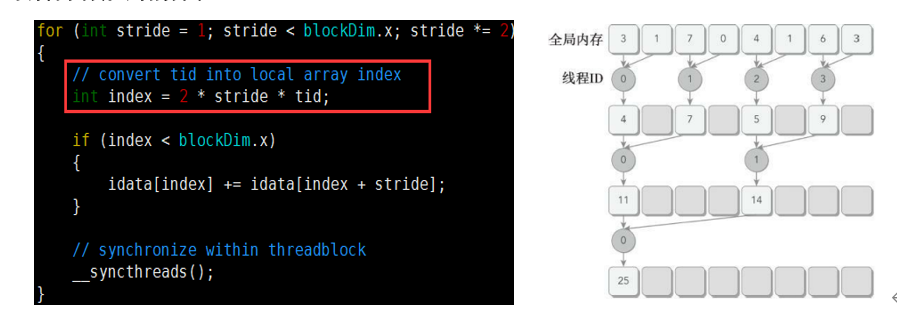
图中红线部分,它为每个线程设置数组访问索引。跨度乘2,使用线程的前半部分来执行求和操作。(例如:512个线程的块,前8个线程束执行第一轮归约,剩下8个什么也不做;第二轮中前4个执行归约,后12个什么也不做,这样就彻底不存在分化了(线程0处理0=0+1,线程1处理2=2+3…),但是在最后五轮中,当每一轮的线程总数小于线程束的大小时,分化就会出现)
2. 交错配对的归约
该方法颠倒了元素的跨度,初始跨度是线程块大小的一半,之后每次迭代中减少一半。与相邻配对方法相比,交错归约的工作线程没有变化,但是每个线程在全局内存中的加载/存储位置是不同的。

For循环中的条件,两个元素跨度被初始化为线程块大小的一半,每次循环都减少一半。
3. 展开循环
循环展开是一个尝试通过减少分支出现的频率和循环维护指令来优化循环的技术。在循环展开中,循环主体在代码中要多次被编写,不是只编写一次循环主体再使用另一个循环来反复执行的。
(1) 展开的归约
交错配对的归约核函数中每个线程只处理一部分数据,这些数据可被认为是一个数据块。
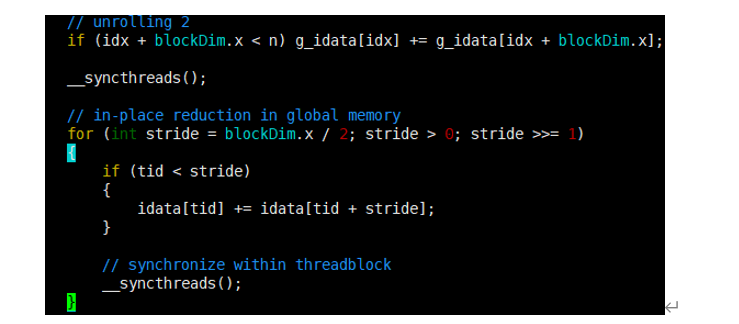
If语句的计算,每个线程都添加一个来自相邻数据块的元素。(相邻的两个block块相加,将结果存储在第一个block块中->相当于相邻两个block块先相加)(可作为归约循环的一个迭代,该循环可在数据块间归约)

全局数组索引被相应地调整,因为只需要一半的线程块来处理相同的数据集。因现在每个线程块处理两个数据块,需要调整内核的执行配置,将网格大小减小至一半。(展开两块)
If语句的计算,每个线程都添加一个来自相邻数据块的元素。(相邻的四个block块相加,将结果存储在第一个block块中->相当于相邻四个block块先相加)(展开四块)
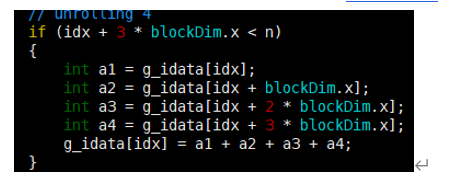
相邻的八个block块相加,将结果存储在第一个block块中->相当于相邻八个block块先相加。(展开八块)
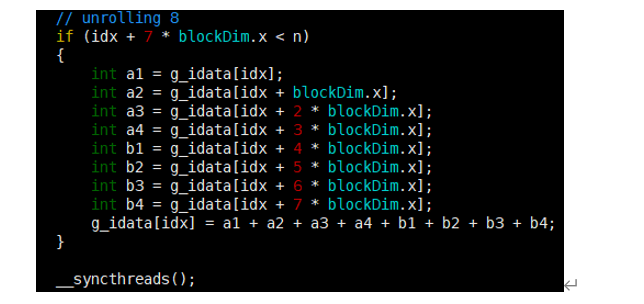
(2) 展开线程的归约
__syncthreads用于块内同步。
在计算时,只剩下32个或更少线程的情况时,线程束的执行时是SIMT的,每条指令之后有隐式的线程束内同步过程,所以归约循环的最后6个迭代进行展开。(注意vemem是volatile修饰的)
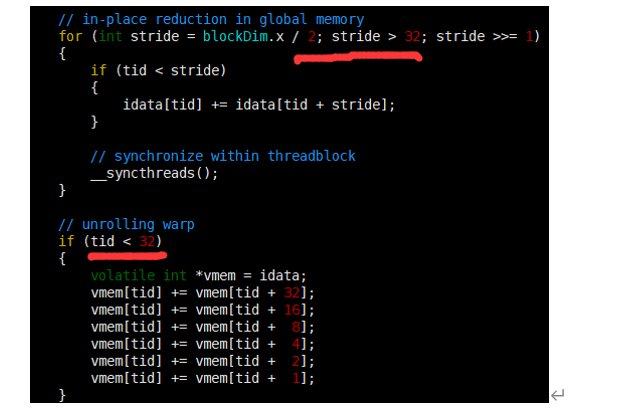
(3) 完全展开的归约
如果编译时时已知一个循环中的迭代次数,就可以把循环完全展开。在Fermi或 Kepler架构中,每个块的最大线程数都是1024,并且在这些归约核函数中循环迭代次数是基于一个线程块维度的,完全展开归约循环是可能的。
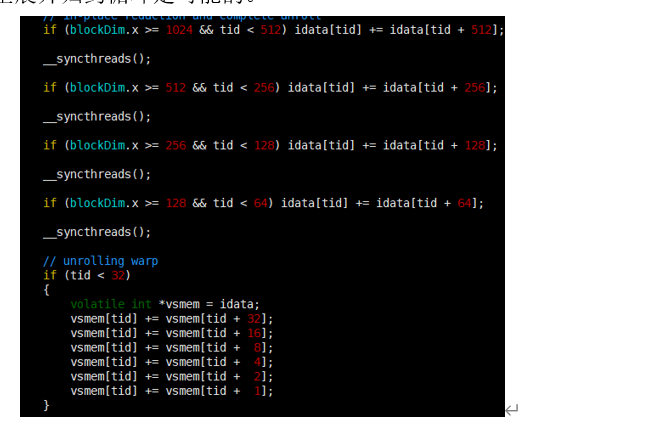
(4) 模板函数的归约
虽然可以手动展开循环,但使用模板函数有助于进一步减少分支消耗。
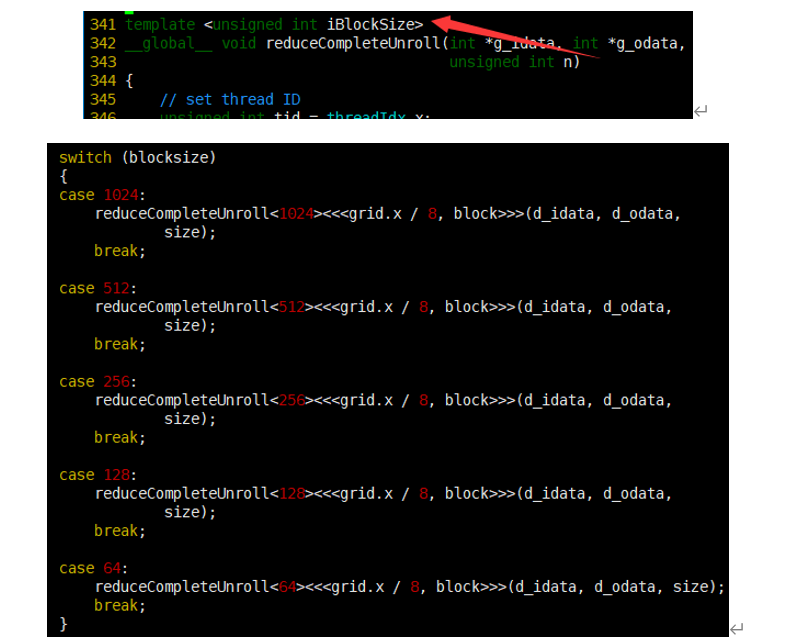
相比reduceCompleteUnrollWarps8,唯一的区别是使用了模板参数替换了块大小。检查块大小的if语句将在编译时被评估,如果这一条件为false,那么编译时它将会被删除,使得内循环更有效率。
4. 结果分析
表归约内核的性能
|
Tesla K80 |
||||
|
内核 |
时间(sec) |
单步加速 |
累计加速 |
grid和block |
|
相邻(分化) |
0.008459 |
|
|
32768 512 |
|
相邻(无分化) |
0.007832 |
1.08005618 |
1.08005618 |
32768 512 |
|
交错 |
0.005033 |
1.556129545 |
1.680707332 |
32768 512 |
|
展开2块 |
0.002877 |
1.749391727 |
2.940215502 |
16384 512 |
|
展开4块 |
0.001452 |
1.981404959 |
5.825757576 |
8192 512 |
|
展开8块 |
0.000892 |
1.627802691 |
9.483183857 |
4096 512 |
|
展开8块+最后的线程束 |
0.000813 |
1.097170972 |
10.40467405 |
4096 512 |
|
展开8块+循环+最后的线程束 |
0.000789 |
1.030418251 |
10.72116603 |
4096 512 |
|
模板化内核 |
0.000777 |
1.015444015 |
10.88674389 |
4096 512 |
加载/存储效率
|
Tesla K80 |
|||
|
内核 |
时间(sec) |
加载效率 |
存储效率 |
|
相邻(分化) |
0.008459 |
96.15% |
95.52% |
|
相邻(无分化) |
0.007832 |
107.54% |
99.40% |
|
交错 |
0.005033 |
25.02% |
25.00% |
|
展开2块 |
0.002877 |
99.21% |
97.71% |
|
展开4块 |
0.001452 |
98.68% |
97.71% |
|
展开8块 |
0.000892 |
98.04% |
97.71% |
|
展开8块+最后的线程束 |
0.000813 |
107.54% |
99.40% |
|
展开8块+循环+最后的线程束 |
0.000789 |
107.54% |
99.40% |
|
模板化内核 |
0.000777 |
25.02% |
25.00% |