1.1 精度与基本数据类型运算的深度解析
我们在探讨Java基本数据类型时多次提到过精度的问题,那么计算机中的精度究竟是什么样的,为什么我们有时候的计算和我们预期的不同呢?下面我们通过精度来了解;
1.1.1 什么是精度,什么是单精度和双精度
百度百科:精度是表示观测值与真值的接近程度。在计算机中精度指的是各种数据类型的位宽。如上我们在做数据类型转换时,如果精度高(数据占用存储空间大的,二进制能够表示位数多的)的数据向精度低的数据转型,那么就会面临着精度损失的危险,而精度低的数据类型向精度高的类型转型则不存在这种问题(我们在1.5.2原始数据类型的基本运算中具体分析数据类型转变的计算机底层原理)。知道了精度,那么单精度和双精度呢?
单精度是这样的格式,1位符号,8位指数,23位小数。
注:指数是幂运算aⁿ(a≠0)中的一个参数,a为底数,n为指数,指数位于底数的右上角,幂运算表示指数个底数相乘。当n是一个正整数,aⁿ表示n个a连乘。当n=0时,aⁿ=1。这里的a为2。

双精度是1位符号,11位指数,52位小数。
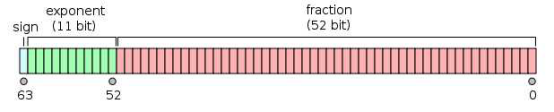
了解了精度,下面我们了解一下类型转换和数据计算的底层是怎样的,为什么运算结果有时会出现意料之外的结果。
1.1.2 计算机你究竟干了啥事
上边我们了解了精度,那么这节我们试着分析一下计算机的底层在类型转换和数据计算时发生了什么,我们先从数据类型开始分析:
1.1.2.1 数据类型转换
数据类型转换分为显示转换和隐式转换,但在计算机中我们将其分为低精度向高精度转变和高精度向低精度转变,这节我们仅针对整数类型来分析,下面来分别看一下;
1.1.2.1.1 低精度向高精度转变
我们通过代码来进行分析,如下:
@org.junit.Test public void fun1(){ byte b1 = 127; byte b2 =-127; int i1 = b1; int i2 = b2; System.out.println("i1="+i1+" i2="+i2); System.out.println(Integer.toBinaryString(i1)); System.out.println(Integer.toBinaryString(i2)); }
byte相对于int来说是一个低精度的数据类型,那么byte转变int,在计算机底层是如何操作的呢?计算机对于整数类型的转变低精度到高精度,会为低精度补足精度,而补充精度有两种补充方式使用补0扩展和使用符号位扩展,详情请阅读补位的两种方式;Java中对于精度扩展使用的是不改变数值的符号扩展,通过控制台打印的结果可以看出,控制台打印结果如下:
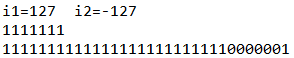
所以我们知道低精度向高精度转换永远也不会出错;
1.1.2.1.2 高精度向低精度转变
上面是低精度向高精度转换,那么高精度向低精度转换呢?高精度向低精度转换,在计算机中会从最低位开始截取直到截取满低精度的精度范围为止,代码如下:
@org.junit.Test public void test2(){ long l = 2345635075023987L; int i = (int) l; System.out.println("高精度向低精度转换是显式转换,可能会出现损失精度问题:"+l); System.out.println("高精度向低精度转换是显式转换,可能会出现损失精度问题:"+i); System.out.println(Integer.toBinaryString(i)); }

long类型的的l变量在计算机中的二进制是:
00000000 00001000 01010101 01010111 10111001 01101011 01100100 01110011
那么高精度向低精度转换,从低位开始截取,int类型是4字节,即32位,为:
10111001 01101011 01100100 01110011
11000110 10010100 10011011 10001100
11000110 10010100 10011011 10001101
可以看出是个负数,原码为:
11000110 10010100 10011011 10001101
结果为:-1184144269
@org.junit.Test public void test4(){ byte b = 127; byte bb = (byte) (b+1); System.out.println("损失精度:"+bb); }
在上面代码中,byte类型经过运算成为了int类型,值为128,此时强制转换为低精度的byte类型,那么就会损失精度:
byte : 01111111
int : 00000000 00000000 00000000 10000000
此时强制转换,将int类型截取8位(byte类型是1个字节),为
10000000
转换为十进制为-128
我们看一个比较有意思的小问题:
@org.junit.Test public void fun2(){ char a = (char) -97;//int --->char 高精度向低精度转变 int i = a; char b = '゚'; String str = "゚"; System.out.println("码点"+str.codePointAt(0)); System.out.println(a); System.out.println(b+0); System.out.println(i); System.out.println(Integer.toBinaryString(a)); System.out.println(Integer.toBinaryString(i)); System.out.println(Integer.toBinaryString(-97)); }

在上面,我们首先给char赋值了一个负值,此时计算机中会将int类型转换为char类型:
11111111111111111111111110011111
1111111110011111
我们知道char可以表示65536个字符(从0到65535),而65535在计算机中的二进制存储为
1111111111111111
我们发现此时二进制首位并没有作为符号位使用,而是作为一个普通的二进制位参与运算,这也和char的功能有关,char表示的是字符,它在计算机中表示的是Unicode中字符对应的码点,码点是从0开始的没有负值。所以我们将-97赋值给char后,实际上计算机中该char存储的是1111111111111111,换算成整数就是65439,而将65439赋值给int,此时以符号位扩充,但是char都是正数,所以实际上是以0扩充,此时我们就能够理解上述结果了。
1.1.2.2 困扰的float和double
在上面我们进行了整数类型的数据类型转换的底层剖析,在这节我们来分析一下float和double,首先我们知道原始数据类型的转换为:
byte < short < int< long < float < double。
注意:byte,short,char之间不会互相转换,他们三者在计算时首先会转换为int类型,有多种类型的数据混合运算时,系统首先自动的将所有数据转换成容量最大的那一种数据类型,然后再进行计算。
下面我们剖析一下float和double在计算机中是如何存储的,
在整数类型中我们知道了整数类型在计算机中的存储,那么浮点型呢?浮点数会和整数类型的存储一致吗?下面我们来了解一下浮点型在计算机中是如何存储的。
对于浮点型的数据采用单精度类型(float)和双精度类型(double)来存储:float 数据占用 32bit;double 数据占用 64bit;
我们在声明一个变量 float f = 2.25f 的时候,是如何分配内存的呢?其实不论是 float 类型还是 double 类型,在存储方式上都是遵从IEEE标准754的规范:float 遵从的是 IEEE R32.24;double 遵从的是 IEEE R64.53;
单精度或双精度在存储中,都分为三个部分:
- 符号位 (Sign):0代表正数,1代表为负数;
- 指数位 (Exponent):用于存储科学计数法中的指数数据;
- 尾数部分 (Mantissa):采用移位存储尾数部分;
单精度 float 的存储方式如下:
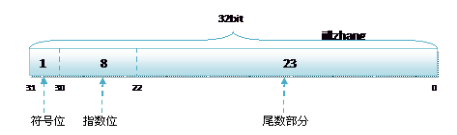
双精度 double 的存储方式如下:
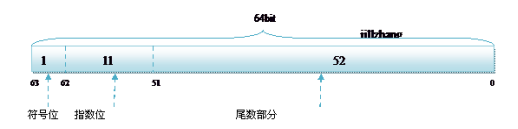
R32.24 和 R64.53 的存储方式都是用科学计数法来存储数据的,比如:
8.25 用十进制表示为:8.25 * 10^0
120.5 用十进制表示为:1.205 * 10^2
而计算机根本不认识十进制的数据,他只认识0和1。所以在计算机存储中,首先要将上面的十进制小数更改为二进制的科学计数法表示:
8.25 用二进制表示为:1000.01
0.25*2=0.5【0】
0.5*2=1.0【1】
118.5 用二进制表示为:1110110.1
0.5*2=1.0【1】
而用二进制的科学计数法表示 1000.1,可以表示为1.0001 * 2^3【位移运算符,左移3位】
而用二进制的科学计数法表示 1110110.1,可以表示为1.1101101 * 2^6
任何一个数的科学计数法表示都为1. xxx * 2^n ,尾数部分就可以表示为xxxx,由于第一位都是1嘛,干嘛还要表示呀?所以将小数点前面的1省略。由此,23bit的尾数部分,可以表示的精度却变成了24bit,道理就是在这里。(float有效位数相应的也会发生变化,而double则不会,因为达不到)
那 24bit 能精确到小数点后几位呢?我们知道9的二进制表示为1001,所以 4bit 能精确十进制中的1位小数点,24bit就能使 float 精确到小数点后6位;
而对于指数部分,因为指数可正可负(占1位),所以8位的指数位能表示的指数范围就只能用7位,范围是:-127至128。所以指数部分的存储采用移位存储,存储的数据为元数据 +127。
注意:元数据+127:大概是指“指数”从00000000开始(表示-127)至11111111(表示+128)
所以,10000000表示指数1 (127 + 1 = 128 --> 10000000 ) ;
指数为 3,则为 127 + 3 = 130,表示为 01111111 + 11 = 10000010 ;
下面就看看 8.25 和 118.5 在内存中真正的存储方式:
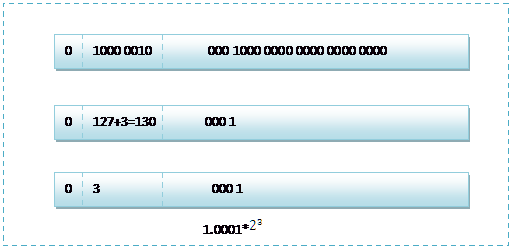
8.25 用二进制表示为:1000.01
8.25 用二进制的科学计数法表示为: 1.0001* 2^3 ,按照上面的存储方式:
符号位为:0,表示为正;
指数位为:3+127=130,即 10000010;
尾数部分为:0001;
故8.25的存储方式如下图所示:
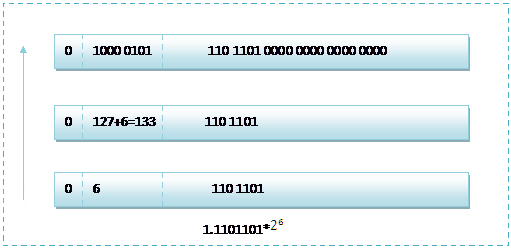
而单精度浮点数118.5的存储方式如下图所示:
那么如果给出内存中一段数据,并且告诉你是单精度存储的话,你将如何知道该数据的十进制数值呢?
其实就是对上面运算的反推过程,比如给出如下内存数据:01000010111011010000000000000000,
首先我们现将该数据分段:0 10000101 11011010000000000000000,在内存中的存储就为下图所示:
根据我们的计算方式,可以计算出这样一组数据表示为:
1.1101101*2^(133-127=6) = 1.1101101 * 2^6 = 1110110.1=118.5
而双精度浮点数的存储和单精度的存储大同小异,不同的是指数部分和尾数部分的位数。所以这里不再详细的介绍双精度的存储方式了,只将118.5的最后存储方式图给出:
下面就这个知识点来解决一个疑惑,请看下面一段程序,注意观察输出结果:
public class Test { public static void main(String[] args) { float f = 2.2f; double d = (double)f; System.out.println(Double.toString(d)); //结果:2.200000047683716 f = 2.25f; d = (double)f; System.out.println(Double.toString(d)); //结果:2.25 //2.25 - 2.2 = 0.05 ( 理想结果0.05 ) System.out.println(2.25 - 2.2);//结果:0.04999999999999982 float f2 = 2.25f - 2.2f; System.out.println(Double.toString(f2)); //结果:0.04999995231628418 } }
输出的结果可能让大家疑惑不解:
单精度的 2.2 转换为双精度后,精确到小数点后13位之后变为了2.2000000476837
而单精度的 2.25 转换为双精度后,变为了2.2500000000000
为何 2.2 在转换后的数值更改了,而 2.25 却没有更改呢?
其实通过上面关于两种存储结果的介绍,我们大概就能找到答案。
2.25 的单精度存储方式表示为:0 10000001 00100000000000000000000
2.25 的双精度存储方式表示为:
0 10000000 0010010000000000000000000000000000000000000000000000000
这样 2.25 在进行强制转换的时候,数值是不会变的。
而我们再看看 2.2,用科学计数法表示应该为:
将十进制的小数转换为二进制的小数的方法是:将小数*2,取整数部分。
0.2×2=0.4,所以二进制小数第一位为0.4的整数部分0;
0.4×2=0.8,第二位为0.8的整数部分0;
0.8×2=1.6,第三位为1;
0.6×2=1.2,第四位为1;
0.2×2=0.4,第五位为0;
...... 这样永远也不可能乘到=1.0,得到的二进制是一个无限循环的排列 00110011001100110011...
对于单精度数据来说,尾数只能表示 24bit 的精度,所以2.2的 float 存储为:
但是这种存储方式,换算成十进制的值,却不会是2.2。因为在十进制转换为二进制的时候可能会不准确(如:2.2),这样就导致了误差问题!并且 double 类型的数据也存在同样的问题!所以在浮点数表示中,都可能会不可避免的产生些许误差!
在单精度转换为双精度的时候,也会存在同样的误差问题。而对于有些数据(如2.25),在将十进制转换为二进制表示的时候恰好能够计算完毕,所以这个误差就不会存在,也就出现了上面比较奇怪的输出结果。
总结:float和double类型主要是为了科学计算和工程计算而设计的。它们执行二进制浮点运算(binary floating-point arithmetic),这是为了在广泛的数值范围上提供较为精确的快速近似计算而设计的。然而,它们并没有提供完全精确的结果,所以不应该被用于需要精确结果的场合。Float和double类型尤其不适合用于货币计算。应该使用BigDecimal,后面我们在常见对象中介绍。