首先,看下Smote算法之前,我们先看下当正负样本不均衡的时候,我们通常用的方法:
- 抽样
常规的包含过抽样、欠抽样、组合抽样
过抽样:将样本较少的一类sample补齐
欠抽样:将样本较多的一类sample压缩
组合抽样:约定一个量级N,同时进行过抽样和欠抽样,使得正负样本量和等于约定量级N
这种方法要么丢失数据信息,要么会导致较少样本共线性,存在明显缺陷
- 权重调整
常规的包括算法中的weight,weight matrix
改变入参的权重比,比如boosting中的全量迭代方式、逻辑回归中的前置的权重设置
这种方式的弊端在于无法控制合适的权重比,需要多次尝试
- 核函数修正
通过核函数的改变,来抵消样本不平衡带来的问题
这种使用场景局限,前置的知识学习代价高,核函数调整代价高,黑盒优化
- 模型修正
通过现有的较少的样本类别的数据,用算法去探查数据之间的特征,判读数据是否满足一定的规律
比如,通过线性拟合,发现少类样本成线性关系,可以新增线性拟合模型下的新点
实际规律比较难发现,难度较高
算法基本原理:
(1)对于少数类中每一个样本x,以欧氏距离为标准计算它到少数类样本集中所有样本的距离,得到其k近邻。
(2)根据样本不平衡比例设置一个采样比例以确定采样倍率N,对于每一个少数类样本x,从其k近邻中随机选择若干个样本,假设选择的近邻为xn。
(3)对于每一个随机选出的近邻xn,分别与原样本按照如下的公式构建新的样本。
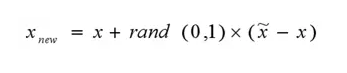
Smote算法的思想其实很简单,先随机选定n个少类的样本,如下图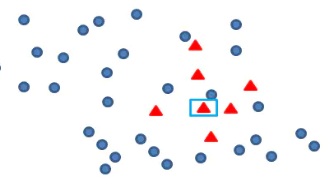
再找出最靠近它的m个少类样本,如下图
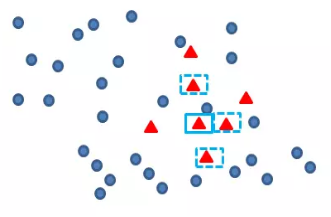
再任选最临近的m个少类样本中的任意一点,
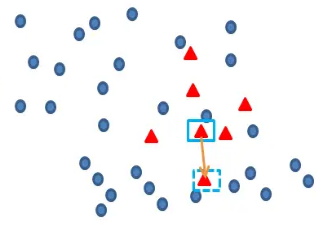
伪代码:
function SMOTE(T, N, k)
Input: T; N; k # T:少数类样本数目
# N:过采样的数目
# K:最近邻的数量
Output: (N/100) * T # 合成的少数类样本
Variables: Sample[][] # 存放原始少数类样本
newindex #控制合成数量
initialized to 0;
Synthetic[][]
if N < 100 then
Randomize the T minority class samples
T = (N/100)*T
N = 100
end if
N = (int)N/100 # 假定SMOTE的数量是100的整数倍
for i = 1 to T do
Compute k nearest neighbors for i, and save the indices in the nnarray
POPULATE(N, i, nnarray)
end for
end function
Algorithm 2 Function to generate synthetic samples
function POPULATE(N, i, nnarray)
Input: N; i; nnarray # N:生成的样本数量
# i:原始样本下标
# nnarray:存放最近邻的数组
Output: N new synthetic samples in Synthetic array
while N != 0 do
nn = random(1,k)
for attr = 1 to numattrs do # numattrs:属性的数量
Compute: dif = Sample[nnarray[nn]][attr] − Sample[i][attr]
Compute: gap = random(0, 1)
Synthetic[newindex][attr] = Sample[i][attr] + gap * dif
end for
newindex + +
N − −
end while
end function
项目经验:
1.采样方法比直接调整阈值的方法要好。
2.使用采样方法可以提高模型的泛化能力,存在过拟合风险,最好联合正则化同时使用。
3.过采样结果比欠采样多数时间稳定,但是还是要具体问题具体分析,主要还是看数据的分布,SMOTE效果还是不错的。
4.和SMOTE算法使用的模型最好是可以防止过拟合的模型,随机森林,L2正则+逻辑回归,XGBoost等模型。