现实生活中的数据集中的样本通常在某系属性上是缺失的,如果属性值缺失的样本数量比较少,我们可以直接简单粗暴的把不完备的样本删除掉,但是如果有大量的样本都有属性值的缺失,那么就不能简单地删除,因为这样删除了大量的样本,对于机器学习模型而言损失了大量有用的信息,训练出来的模型性能会受到影响。这篇博客就来介绍在决策树中是如何处理属性值有缺失的样本的,本篇博客使用的数据集如下(数据集来自周志华《机器学习》):
在决策树中处理含有缺失值的样本的时候,需要解决两个问题:
如何在属性值缺失的情况下进行划分属性的选择?(比如“色泽”这个属性有的样本在该属性上的值是缺失的,那么该如何计算“色泽”的信息增益?)
给定划分属性,若样本在该属性上的值是缺失的,那么该如何对这个样本进行划分?(即到底把这个样本划分到哪个结点里?)
下面就来介绍如何解决这两个问题:

比较发现,“纹理”在所有属性中的信息增益值最大,因此,“纹理”被选为划分属性,用于对根节点进行划分。划分结果为:“纹理=稍糊”分支:{7,9,13,14,17},“纹理=清晰”分支:{1,2,3,4,5,6,15},“纹理=模糊”分支:{11,12,16}。如下图所示:
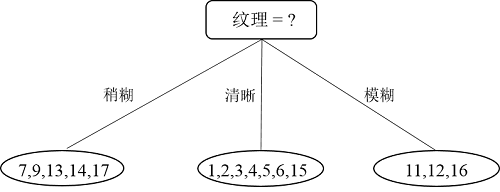
那么问题来了,编号为{8,10}的样本在“纹理”这个属性上是缺失的,该被划分到哪个分支里?前面讲过了,这两个样本会同时进入到三个分支里,只不过进入到每个分支后权重会被调整(前面也说过,在刚开始时每个样本的权重都初始化为1)。编号为8的样本进入到三个分支里后,权重分别调整为5/15,7/15 和 3/15;编号为10的样本同样的操作和权重。因此,经过第一次划分后的决策树如下图所示:

我们都知道构造决策树的过程是一个递归过程,原来不打算继续介绍递归过程了,但是因为权重发生了变化,所以继续介绍下递归过程。接下来,递归执行“纹理=稍糊”这个分支,样本集D = {7,8,9,10,13,14,17},共7个样本。如下图所示:

下面来看具体的计算过程:

对比能够发现属性“敲声”的星系增益值最大,因此选择“敲声”作为划分属性,划分后的决策树如下图所示:
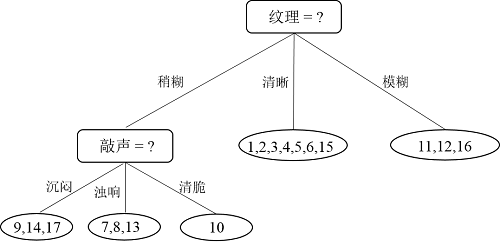
接下来对分支{敲声 = 沉闷}即结点{9,14,17}进行划分,根据博客决策树(一)介绍的三种递归返回情形,结点{9,14,17}因为包含的样本全部属于同一类别,因此无需划分,直接把结点{9,14,17}标记为叶结点,如下图所示:
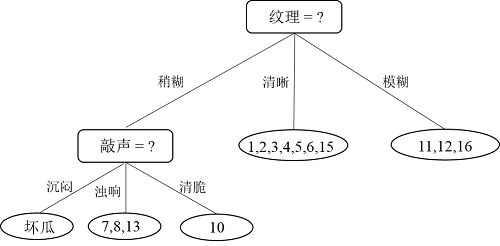
根据递归过程,接下来对分支“敲声 = 浊响”即结点{7,8,13}进行划分,计算过程和上面一样,虽然我也算过了,但是不再贴出来了,需要注意的是样本的权重是1/3。计算完比较能够知道属性“脐部”的信息增益值最大,因此选择“脐部”作为划分属性,划分完的决策树如下图所示:
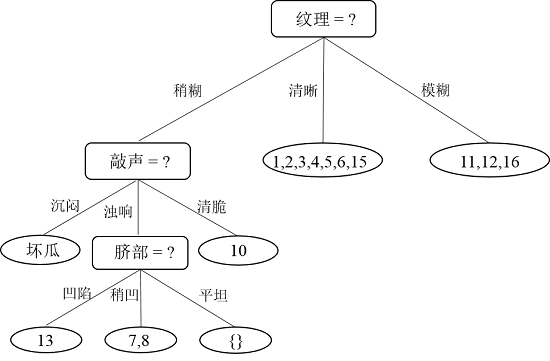
接下来,继续,对于结点{13},因为就一个样本了,直接把该结点标记为叶结点,类别为“坏瓜”;递归到结点{7,8},因为样本类别相同,所以也标记为叶结点,类别为“好瓜”;递归到结点“脐部=平坦”,因为这个结点不包含任何样本为空集,因此,把该结点标记为叶结点,类别设置为父节点中多数类的类别,即为“好瓜”。因此“纹理=稍糊”这颗子树构造完毕,如下图所示:

接下来,只需递归的重复上述过程即可,即能训练出一颗完整的决策树,最终的决策树如下图所示(该图片来自西瓜书):
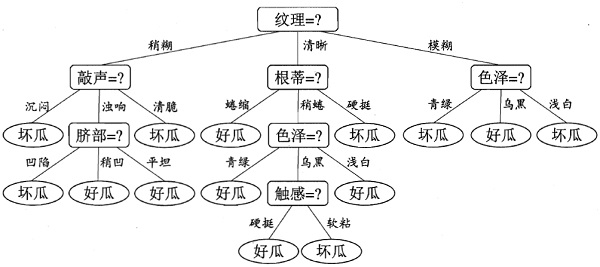
以上介绍了决策树在训练阶段是如何处理有缺失值的样本的,从而构造出一颗树。当我们构造完一棵树后,有新的样本过来就可以对新的样本进行分类了,那么问题来了,如果测试样本属性也有缺失值那要怎么办?
如果有专门处理缺失值的分支,就走这个分支。
用这篇论文提到的方法来确定属性a的最有可能取值,然后走相应的分支。
从属性a最常用的分支走
同时探查所有的分支,并组合他们的结果来得到类别对应的概率,(取概率最大的类别)
将最有可能的类别赋给该样本。
上面的这么多方法只是提一下,C4.5中采用的方法是:测试样本在该属性值上有缺失值,那么就同时探查(计算)所有分支,然后算每个类别的概率,取概率最大的类别赋值给该样本。好像这个方法并不怎么好用语言描述,我们直接看例子吧,相信你看完例子就立刻明白了,由于这是今天(19年4月9号)新添加的内容,上面西瓜书上的例子当时计算的权重没有保留下来,因此这里直接引用Quinlan在著作《C4.5: Programs For Machine Learning》里举的例子(在该书的p31-p32),先看数据集:
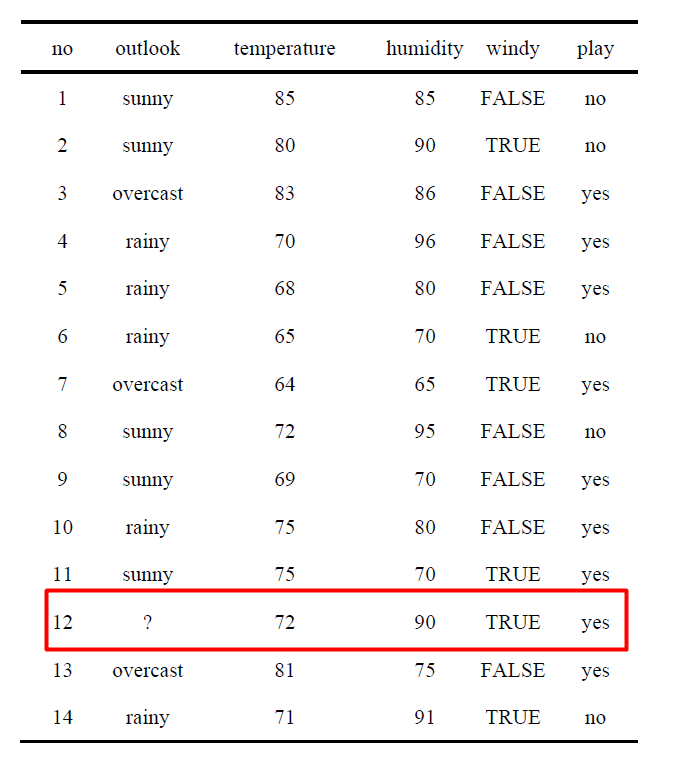
注意,编号12的样本属性outlook上有缺失值,我们基于上面介绍的构造决策树的方法来构造一颗决策树(C4.5用信息增益率,除此之外,构造方法与上述方法一致),构造出来的决策树为:
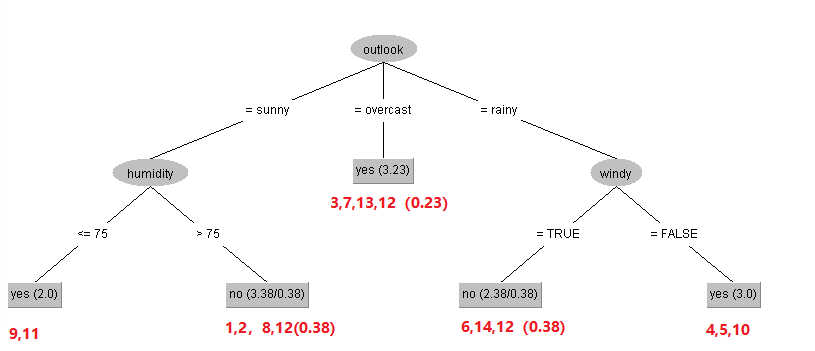
上图中,红色数字表示样本编号,括号内的值表示样本12的权重。叶结点中的数值(N/E),比如no(3.38/0.38)表示这个叶子节点被标记为no也就是don't play,3.38=1+1+0.38,编号1,2的样本没有缺失值,权重为1进来的,编号12进入到这个叶结点时权重为0.38。
如果,此时我们有一条样本:outlook=sunny, temperature=70, humidity=?, windy=false 能够看出这条样本的属性humidity是缺失的,那么构建好的决策怎么对这个样本分类?
首先这个样本的outlook为sunny,肯定会进入到“humidity”这个节点里,因为该样本humidity属性值缺失,两个分支都有可能进入:
如果humidity<=75,则类别为play。
如果humidity>75,don't play的概率为3/3.38=88.7%,play的概率为0.38/3.38=11.3%。
大家肯定有一点疑惑,就是上面humidity>75里,明明叶结点的label为no啊,那应该是don't play啊,怎么还有don't play和paly的概率,这是Quinlan的定义,上面的(N/E)中,N,E的定义分别是:
N表示该叶节点中所包含的总样本数(总权重更恰当点)
E表示与该叶节点的类别不同的样本数(权重),比如上面第二个叶结点的label为no(dont play),包含的样本数为1,2,8,12(0.38),这里编号12的样本类别为play,因此与该叶结点的类别不同,所以这叶结点会产生11.3%的概率为play。
那么根据上面介绍的,此时同时探查(计算)所有分支,然后算每个类别的概率,取概率最大的类别赋值给该样本。这里humidity下就有两个分支,<=75 => yes 和 >75 =>no。下面分别计算这两个类别的概率:
yes(play):2.0/5.38 * 100% + 3.38/5.38 * 11.3% = 44.27%
no(don't play): 3.38/5.38 * 88.7% = 55.73%
因此no的概率更大,所以该测试样本的类别被指派为no,即don't play。