fftshift函数详解

reference: https://ww2.mathworks.cn/help/matlab/ref/fftshift.html

一.实信号情况

因为实信号以fs为采样速率的信号在 fs/2处混叠，所以实信号fft的结果中前半部分对应[0, fs/2],后半部分对应[ -fs/2, 0]；

1）实信号fft的结果前半部分对应[0, fs/2]是正频率的结果,后半部分对应[ -fs/2, 0]是负频率的结果。大于fs/2的部分的频谱实际上是实信号的负频率加fs的结果。故要得到正确的结果，只需将视在频率减去fs即可得到频谱对应的真实负频率；

2）如果要让实信号fft的结果与[-fs/2, fs/2]对应，则要fft后fftshift一下即可，fftshift的操作是将fft结果以fs/2为中心左右互换；

3）如果实信号fft的绘图频率f从[-fs/2, fs/2]，并且没有fftshift，则fft正频谱对应f在[0, fs/2]的结果将混叠到(f - fs/2)的位置;

fft负频谱对应f在[-fs/2, 0]的结果混叠到 f + fs - fs/2 的位置，注意这里f为负值，也就是说此种情况下fft负频谱对应的视在频率减去fs/2即可得到频谱对应的真实负频率。

 

二.复信号情况

1）复信号没有负频率，以fs为采样速率的信号，fft的频谱结果是从[0,fs]的。

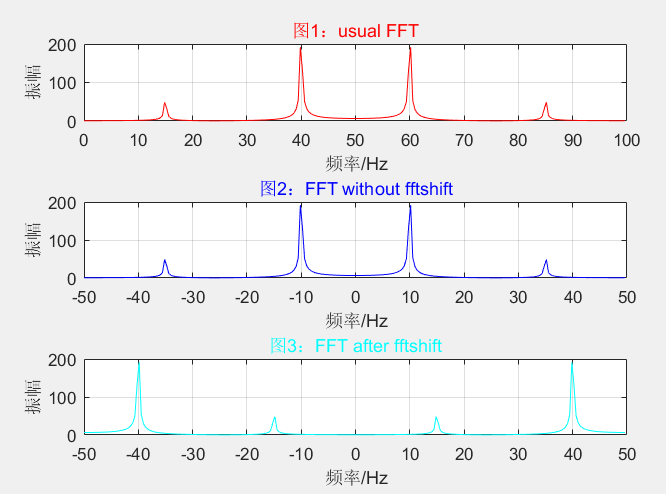
2）在 f> fs/2时，对复信号的fft结果进行fftshift会产生频率混叠(将下面的示例2中的频率从f=15改为f=85可以验证f=85的谱线在fftshift后跑到 f= -15 = 85 - fs = 85 - 100的位置了)，所以复信号也一般要求 f <= fs/2

3）在对雷达的慢时间维(复信号)进行fft后，由于要用doppler= ((0:LFFT-1)/LFFT  - 0.5)*PRF; 计算多普勒频率，所以对该慢时间信号fft后要fftshift下，以便和正确的频率单元相对应。注意多普勒频率fd < = PRF/2 时才测的准！

 

fftshift

作用：将零频点移到频谱的中间

用法：

Y=fftshift(X)
Y=fftshift(X，dim)

描述：fftshift移动零频点到频谱中间，重新排列fft,fft2和fftn的输出结果。将零频点放到频谱的中间对于观察傅立叶变换是有用的。

示例1 -实信号的情况：

clf;

fs=100;N=256;   %采样频率和数据点数
n=0:N-1;t=n/fs;   %时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号

y1=fft(x,N);    %对信号进行快速Fourier变换
y2=fftshift(y1);

mag1=abs(y1);     %求得Fourier变换后的振幅
mag2=abs(y2);    

f1=n*fs/N;    %频率序列
f2=n*fs/N-fs/2;

subplot(3,1,1),plot(f1,mag1,'r');  %绘出随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('图1：usual FFT','color','r');grid on;

subplot(3,1,2),plot(f2,mag1,'b');  %绘出随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('图2：FFT without fftshift','color','b');grid on;

subplot(3,1,3),plot(f2, mag2,'c');  %绘出随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('图3：FFT after fftshift','color','c');grid on;

　　

结论：

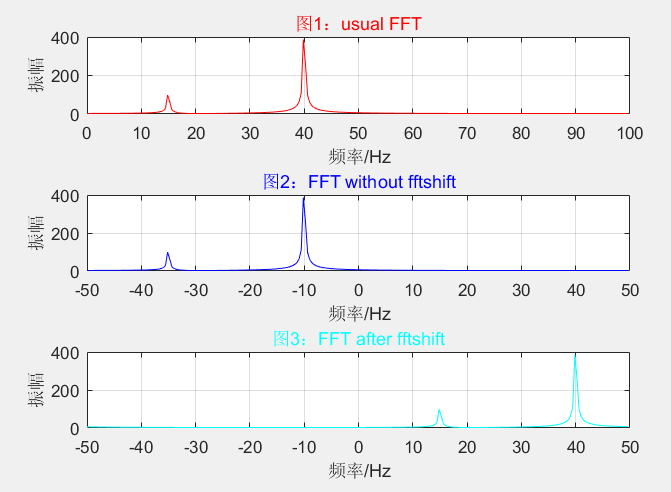
1）如果期望绘制的幅频图的频率范围为0~fs，则无需运行fftshift变换，正频率对应在[0, fs/2],大于fs/2的频谱的频率值为对应[-fs/2  , 0 ]负频率f + fs，注意f是负频率，是个负数。如图1。

2）如果期望绘制的幅频图的频率范围为-fs/2~fs/2，则需要运行fftshift变换，如图3；如果不变换，图示的响应频点会发生变换，如图2，分析见顶端。

 

 

示例2 -复信号的情况：

close all; clear; clf;

fs=100;N=256;   %采样频率和数据点数
n=0:N-1;t=n/fs;   %时间序列
x=0.5*exp(j*2*pi*15*t)+2*exp(j*2*pi*40*t); %信号

y1=fft(x,N);    %对信号进行快速Fourier变换
y2=fftshift(y1);

mag1=abs(y1);     %求得Fourier变换后的振幅
mag2=abs(y2);    

f1=n*fs/N;    %频率序列
f2=n*fs/N-fs/2;

subplot(3,1,1),plot(f1,mag1,'r');  %绘出随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('图1：usual FFT','color','r');grid on;

subplot(3,1,2),plot(f2,mag1,'b');  %绘出随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('图2：FFT without fftshift','color','b');grid on;

subplot(3,1,3),plot(f2,mag2,'c');   %绘出随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('图3：FFT after fftshift','color','c');grid on;