在程序设计中经常会执行查找操作,有时需要在庞大的数据库中查找某一条记录,这时查找时间就显得尤为重要,怎么样才能节省查找时间?提高查找效率呢,下面我们来看一下常用的一些查找算法。
【顺序查找】
一 、概念
从表的一端开始,顺序扫描线性表,依次将扫描到的结点关键宇和给定值K相比较。若当前扫描到的结点关键字与K相等,则查找成功;若扫描结束后,仍未找到关键字等于K的结点,则查找失败。
二、特点
它查找表的存储结构:既适用于顺序存储结构,也适用于链式存储结构。
那么我们怎么知道一个算法好坏呢,在这里我们利用时间复杂度和空间复杂度表示,又由于空间复杂度一般是相同的,就不予考虑,我们只考虑时间复杂度,我们可以用平均查找长度ASL表示:如下面公式
在等概率情况下,pi=1/n(1≤i≤n),故成功的平均查找长度为
n+1)/2
【二分查找】
一、二分查找(Binary Search)
二分查找又称折半查找,它是一种效率较高的查找方法。
二分查找要求:线性表是有序表,即表中结点按关键字有序,并且要用向量作为表的存储结构。
二、二分查找的基本思想
二分查找的基本思想是:(设R[low..high]是当前的查找区间)
(1)首先确定该区间的中点位置:
![]()
(2)然后将待查的K值与R[mid].key比较:若相等,则查找成功并返回此位置,否则须确定新的查找区间,继续二分查找,具体方法如下:
①若R[mid].key>K,则由表的有序性可知R[mid..n].keys均大于K,因此若表中存在关键字等于K的结点,则该结点必定是在位置mid左边的子表R[1..mid-1]中,故新的查找区间是左子表R[1..mid-1]。
②类似地,若R[mid].key<K,则要查找的K必在mid的右子表R[mid+1..n]中,即新的查找区间是右子表R[mid+1..n]。下一次查找是针对新的查找区间进行的。
因此,从初始的查找区间R[1..n]开始,每经过一次与当前查找区间的中点位置上的结点关键字的比较,就可确定查找是否成功,不成功则当前的查找区间就缩小一半。这一过程重复直至找到关键字为K的结点,或者直至当前的查找区间为空(即查找失败)时为止。
三、二分查找判定树
二分查找过程可用二叉树来描述:把当前查找区间的中间位置上的结点作为根,左子表和右子表中的结点分别作为根的左子树和右子树。由此得到的二叉树,称为描述二分查找的判定树(Decision Tree)或比较树(Comparison Tree)。
(1)二分查找判定树的组成
①圆结点即树中的内部结点。树中圆结点内的数字表示该结点在有序表中的位置。
②外部结点:圆结点中的所有空指针均用一个虚拟的方形结点来取代,即外部结点。
③树中某结点i与其左(右)孩子连接的左(右)分支上的标记"<"、"("、">"、")"表示:当待查关键字K<R[i].key(K>R[i].key)时,应走左(右)分支到达i的左(右)孩子,将该孩子的关键字进一步和K比较。若相等,则查找过程结束返回,否则继续将K与树中更下一层的结点比较。
(2)二分查找判定树的查找
二分查找就是将给定值K与二分查找判定树的根结点的关键字进行比较。若相等,成功。否则若小于根结点的关键字,到左子树中查找。若大于根结点的关键字,则到右子树中查找。
【例】待查表的关键字序列为:(05,13,19,21,37,56,64,75,80,88,92),若要查找K=85的记录,所经过的内部结点为6、9、10,最后到达方形结点"9-10",其比较次数为3。
实际上方形结点中"i-i+1"的含意为被查找值K是介于R[i].key和R[i+1].key之间的,即R[i].key<K<R[i+1].key。
(3)二分查找的平均查找长度
设内部结点的总数为n=2h-1,则判定树是深度为h=lg(n+1)的满二叉树(深度h不计外部结点)。树中第k层上的结点个数为2k-1,查找它们所需的比较次数是k。因此在等概率假设下,二分查找成功时的平均查找长度为:
ASLbn≈lg(n+1)-1
二分查找在查找失败时所需比较的关键字个数不超过判定树的深度,在最坏情况下查找成功的比较次数也不超过判定树的深度。即为:
![]()
二分查找的最坏性能和平均性能相当接近。
五、二分查找的优点和缺点
虽然二分查找的效率高,但是要将表按关键字排序。而排序本身是一种很费时的运算。既使采用高效率的排序方法也要花费O(nlgn)的时间。
二分查找只适用顺序存储结构。为保持表的有序性,在顺序结构里插入和删除都必须移动大量的结点。因此,二分查找特别适用于那种一经建立就很少改动、而又经常需要查找的线性表。
对那些查找少而又经常需要改动的线性表,可采用链表作存储结构,进行顺序查找。链表上无法实现二分查找。
【分块查找】
一、概念:
分块查找是一种性能介于顺序查找和二分查找之间的一种查找方法,但它要求先对查找表建立一个索引表,再进行分块查找。
二、 索引表建立方法:
先对查找表进行分块,要求"分块有序",即块内关键字不一定有序,但块件间有序。然后,抽取各块中的最大关键字及其起始位置构成一个索引表。如下图:
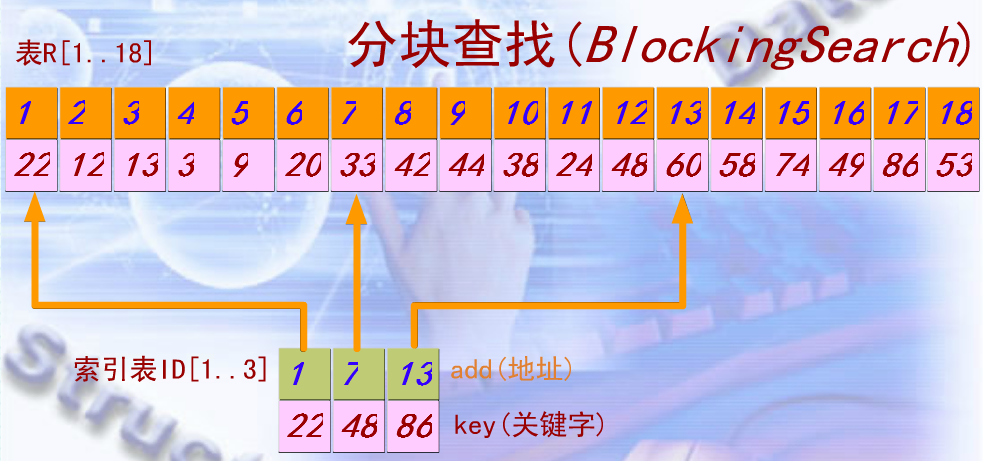
从图中可以看出分开查找主要由两部分组成:索引表和分块序列。
并有如下特点:
A 索引表为有序序列
B 分块间有顺序、块内无序
根据特点可确定它的查找方法:分两步进行,先查找索引表,因其有序,故可采用二分法查找,以确定待查记录在哪一块,然后,在已确定的块中进行再顺序查找。
带入公式则分块查找的平均查找长度为:ASLbs=Lb+Lw=log2(b+1)-1+(s+1)/2 ≈
log2(n/s+1)+ s/2