A. Road To Zero
两个数,将其中一个增加或减少1的代价为a,同时增加或减少1的代价为b,求将两个数同时变为0的最小代价。
当一个数为0或者两个数异号时,最优为只执行代价为a的操作,当两个数同号时,要考虑b与a*2的大小。

#include <bits/stdc++.h> using namespace std; typedef long long ll; #define rep(i, a, b) for (register int i = a; i <= b; i++) ll x, y, a, b; int main() { int t; cin >> t; while (t--) { cin >> x >> y; cin >> a >> b; if (b > a * 2 || x * y <= 0) cout << (abs(x) + abs(y)) * a << endl; else { x = abs(x); y = abs(y); cout << min(x, y) * b + abs(y - x) * a << endl; } } }
B. Binary Period
利用字符串t构造s使t为s的一个子序列,并且使周期k最小,长度不大于t的两倍。
根据题意这样构造出来k只能是1或2。如果t本身具有周期1,直接输出,否则可以在两个相同元素中间插另一个元素,此时s周期为2。

#include <bits/stdc++.h> using namespace std; typedef long long ll; #define rep(i, a, b) for (register int i = a; i <= b; i++) int n; char s[110]; int main() { int t; cin >> t; while (t--) { memset(s, 0, sizeof(s)); cin >> s; n = strlen(s); int flag = 1; rep(i, 1, n - 1) if (s[i] != s[i - 1]) flag = 0; if (flag) cout << s; else rep(i, 0, n - 1) { cout << s[i]; if (s[i] == s[i + 1]) putchar(s[i] == '0' ? '1' : '0'); } cout << endl; } }
C. Yet Another Counting Problem
x∈[l,r], ((x mod a) mod b)≠((x mod b) mod a) 的个数。
考虑预处理前缀和,但是l,r实在是太大了。发现x变化具有周期性,周期为a*b,只用预处理[0,a*b]即可。

#include <bits/stdc++.h> using namespace std; typedef long long ll; #define rep(i, a, b) for (register int i = a; i <= b; i++) ll a, b, q, num[40010]; ll l, r, ans; int main() { int t; cin >> t; while (t--) { cin >> a >> b >> q; rep(i, 1, a * b) { num[i] = (i % a % b != i % b % a) ? 1 : 0; num[i] += num[i - 1]; } while (q--) { cin >> l >> r; ans = (r - l) / (a * b) * num[a * b]; l %= (a * b); r %= (a * b); if (r >= l) cout << ans + num[r] - num[l - 1] << " "; else cout << ans + num[r] + num[a * b] - num[l - 1] << " "; } cout << endl; } }
D. Multiple Testcases
比赛时读了好久才明白题意(wtcl),组合m数组,在满足条件的情况下使ans(组合的数量)最小,条件为一个组合中大于等于i的数不超过c[i]个。
ans挺好找。然后每个组合的元素,按照m[i]从大到小往里面填就行了。

#include <bits/stdc++.h> using namespace std; typedef long long ll; #define rep(i, a, b) for (register int i = a; i <= b; i++) ll n, k, m[200010], c[200010]; ll ans; vector<ll> tmp[200010]; int main() { cin >> n >> k; rep(i, 1, n) cin >> m[i]; rep(i, 1, k) cin >> c[i]; sort(m + 1, m + n + 1); for (int i = n; i; i--) { if (m[i] == m[i - 1]) continue; ans = max(ans, (ll)ceil(1.0 * (n - i + 1) / c[m[i]])); } for (int i = n, j = 0; i; i--, j = (j + 1) % ans) tmp[j].push_back(m[i]); cout << ans << endl; rep(i, 0, ans - 1) { int j = tmp[i].size(); cout << j << " "; rep(z, 0, j - 1) cout << tmp[i][z] << " "; cout << endl; } }
E. Placing Rooks
n*n的格子放n个车,要求所有空格子都在攻击范围、k对车能互相攻击。
所有格子都在攻击范围,那么每一行 / 每一列都要有车。
k对车能相互攻击,那么要空k列不能放车(保证每一行都有一辆车),或者空k行不放车(保证每一列都有车)。
先计算行,问题相当于在n-k列中放n个车,答案为
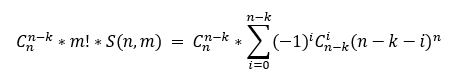
至于为什么是这样计算可以先学习特斯林数和“n个球m个盒子问题”。
当k==0的时候行和列的答案重复了,所以k!=0的时候答案乘2。k>=n时答案为0。

#include <bits/stdc++.h> using namespace std; typedef long long ll; #define rep(i, a, b) for (register int i = a; i <= b; i++) const int mod = 998244353; ll n, k; ll ans; ll fac[200010]; ll ksm(ll a, ll b) { ll res = 1; for (; b; b >>= 1, a = a * a % mod) if (b & 1) res = res * a % mod; return res; } ll C(ll x, ll y) { return fac[x] * ksm(fac[y] * fac[x - y] % mod, mod - 2) % mod; } int main() { fac[0] = 1; cin >> n >> k; rep(i, 1, n) fac[i] = fac[i - 1] * i % mod; if (k >= n) { puts("0 "); return 0; } rep(i, 0, n - k) { ll flag = i & 1 ? -1 : 1; ll tmp = flag * (C(n - k, i) * ksm(n - k - i, n) % mod); ans = (ans + tmp + mod) % mod; } if (k == 0) cout << ans << endl; else cout << (ans * C(n, n - k) % mod) * 2 % mod << endl; }
