快速幂

一．前言

...

二．快速幂

幂运算是一种常见的运算，最容易想到的累乘法的复杂度为O(n)，但很多时候这并不够快，所以出现了快速幂运算。

（为什么不用内置函数pow？）有时候幂运算结果特别大，超出了longlong的范围，这时候答案会要求你取模，这时候用pow函数是肯定不行的。

快速幂运用了倍增的思想，用式子理解就是：

 

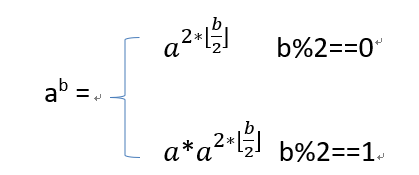
利用这个特性，重复a=a²，b=b/2，我们可以轻松的写出快速幂：

int ksm(int a, int b)
{
    int res = 1;
    while (b > 0)
    {
        if (b % 2 == 1)
            res *= a;
        b /= 2;
        a *= a;
    }
    return res;
}

例如：

res=1,　　a=3,　　 b=5（初始状态）

res=3,　　a=9,　　 b=2（b=5为奇数，res*=a）

res=3,　　a=81,　   b=1（b=2 为偶数，res不变）

res=243,   a=81*81,  b=0（res*=a，退出循环，3⁵=243）

模板如下O(logn)：

int ksm(int a, int b,int mod){
    int res=1;
    for(;b;b>>=1,a=a*a%mod)if(b&1)res=res*a%mod;
    return res;
}

　　

三．矩阵快速幂

在矩阵快速幂之前，先了解下斐波拉契（Fibonacci）数列：

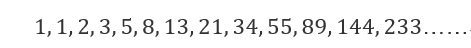
在这个数列中，从第三项开始，每一项都等于前两项之和。不难想出计算方法：

int f(int k)
{
    return k > 2 ? f(k - 1) + f(k - 2) : 1;
}

递归进行了大量重复计算，使用递推：

int f(int k)
{
    int a[k + 2];
    a[1] = a[2] = 1;
    for (int i = 3; i <= k; i++)
        a[i] = a[i - 1] + a[i - 2];
    return a[k];
}

 复杂度为O(n)，能否想出更好的方法，其实是有的！那么怎么使用快速幂才能计算呢？我们试着把斐波拉契转化为矩阵形式：

这时候我们已经可以看出来了，实际上矩阵快速幂就是对矩阵进行快速幂计算

代码如下：

struct Matrix //用结构体储存矩阵
{
    long long mat[2][2];
};
Matrix mul_M(Matrix a, Matrix b, int mod) //定义矩阵乘法
{
    Matrix ret;
    for (int i = 0; i < 2; i++)
        for (int j = 0; j < 2; j++)
        {
            ret.mat[i][j] = 0;
            for (int k = 0; k < 2; k++)
            {
                ret.mat[i][j] += a.mat[i][k] * b.mat[k][j] % mod;
                if (ret.mat[i][j] >= mod)
                    ret.mat[i][j] %= mod;
            }
        }
    return ret;
}
Matrix pow_M(Matrix a, int b, int mod) //快速幂
{
    Matrix ret;
    memset(ret.mat, 0, sizeof(ret.mat));
    for (int i = 0; i < 2; i++)
        ret.mat[i][i] = 1;
    Matrix tmp = a;
    while (b)
    {
        if (b & 1)
            ret = mul_M(ret, tmp, mod);
        b >>= 1;
        tmp = mul_M(tmp, tmp, mod);
    }
    return ret;
}
int f(int n)
{
    Matrix sd = {1, 1, 1, 0}; //初始化矩阵
    sd = pow_M(sd, n - 2, 1e9 + 7);
    return sd.mat[0][0] + sd.mat[0][1];
}

四．十进制快速幂

我们来看看下面这道题：

给四个正整数x₀，x₁，a，b，n，MOD，已知 x_i = a*x_i-1 + b*x_i-2 ( i>=2 )  计算 x_n

乍一看这不就是矩阵快速幂吗，别急还没给范围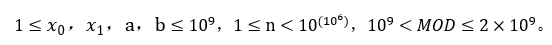 

n这么大一定只能用字符串保存，那怎么模拟除2的操作呢 /汗 ，实际上快速幂用的是2进制的倍增，我们只需要使用十进制的倍增就可以很好的还原这个操作了。

struct Matrix //用结构体储存矩阵
{
    long long mat[2][2];
};
Matrix mul_M(Matrix a, Matrix b, long long mod) //定义矩阵乘法
{
    Matrix ret;
    for (int i = 0; i < 2; i++)
        for (int j = 0; j < 2; j++)
        {
            ret.mat[i][j] = 0;
            for (int k = 0; k < 2; k++)
            {
                ret.mat[i][j] += a.mat[i][k] * b.mat[k][j] % mod;
                if (ret.mat[i][j] >= mod)
                    ret.mat[i][j] %= mod;
            }
        }
    return ret;
}
Matrix pow_M(Matrix a, int b, long long mod) //快速幂
{
    Matrix ret;
    memset(ret.mat, 0, sizeof(ret.mat));
    for (int i = 0; i < 2; i++)
        ret.mat[i][i] = 1;
    Matrix tmp = a;
    while (b)
    {
        if (b & 1)
            ret = mul_M(ret, tmp, mod);
        b >>= 1;
        tmp = mul_M(tmp, tmp, mod);
    }
    return ret;
}
int f(int x0, int x1, int a, int b, char n[1000010], long long MOD)
{
    Matrix sd = {0, b, 1, a}; //初始化矩阵
    Matrix ans = {1, 0, 0, 1};
    for (int i = strlen(n) - 1; i >= 0; i--)
    {
        if (n[i] != '0')
            ans = mul_M(ans, pow_M(sd, n[i] - '0', MOD), MOD);
        sd = pow_M(sd, 10, MOD);
    }
    return (1ll * x0 * ans.mat[0][0] + 1ll * x1 * ans.mat[1][0]) % MOD;
}