Floyd算法

转自https://blog.csdn.net/qq_35644234/article/details/60875818

1、最短路径问题介绍

问题解释：
从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径，称为最短路径

解决问题的算法：

• 迪杰斯特拉算法（Dijkstra算法）
• 弗洛伊德算法（Floyd算法）
• SPFA算法

之前已经对Dijkstra算法做了介绍（不懂的可以看这篇博客：Dijkstra算法详解），所以这篇博客打算对Floyd算法做详细的的介绍。

2、Floyd算法的介绍（动态规划）

  通过这种方法我们可以求出任意两个点之间最短路径。它的时间复杂度是O(N³)。令人很震撼的是它竟然只有五行代码，实现起来非常容易。正是因为它实现起来非常容易，如果时间复杂度要求不高，使用Floyd-Warshall来求指定两点之间的最短路或者指定一个点到其余各个顶点的最短路径也是可行的。当然也有更快的算法，请看下一节：Dijkstra算法。

       另外需要注意的是：Floyd-Warshall算法不能解决带有“负权回路”（或者叫“负权环”）的图，因为带有“负权回路”的图没有最短路。例如下面这个图就不存在1号顶点到3号顶点的最短路径。因为1->2->3->1->2->3->…->1->2->3这样路径中，每绕一次1->-2>3这样的环，最短路就会减少1，永远找不到最短路。其实如果一个图中带有“负权回路”那么这个图则没有最短路。

• 算法的特点：
  弗洛伊德算法是解决任意两点间的最短路径的一种算法，可以正确处理有向图或无向图或负权（但不可存在负权回路)的最短路径问题，同时也被用于计算有向图的传递闭包。

• 算法的思路

　　通过Floyd计算图G=(V,E)中各个顶点的最短路径时，需要引入两个矩阵，矩阵D中的元素d[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。矩阵P中的元素p[i][j]，表示顶点i到顶点j经过了p[i][j]记录的值所　　表示的顶点。

　　假设图G中顶点个数为N，则需要对矩阵D和矩阵P进行N次更新。初始时，矩阵D中顶点d[i][j]的距离为顶点i到顶点j的权值；如果i和j不相邻，则d[i][j]=∞，矩阵P的值为顶点p[i][j]的j的值。 接下来开始，对矩　　阵D进行N次更新。第1次更新时，如果”d[i][j]的距离” > “d[i][0]+d[0][j]”(d[i][0]+d[0][j]表示”i与j之间经过第1个顶点的距离”)，则更新d[i][j]为”d[i][0]+d[0][j]”,更新p[i][j]=p[i][0]。 同理，第k次更新时，如果”d[i][j]的　　距离” > “d[i][k-1]+d[k-1][j]”，则更新d[i][j]为”d[i][k-1]+d[k-1][j]”,p[i][j]=p[i][k-1]。更新N次之后，操作完成！

 

3、Floyd算法的实例过程

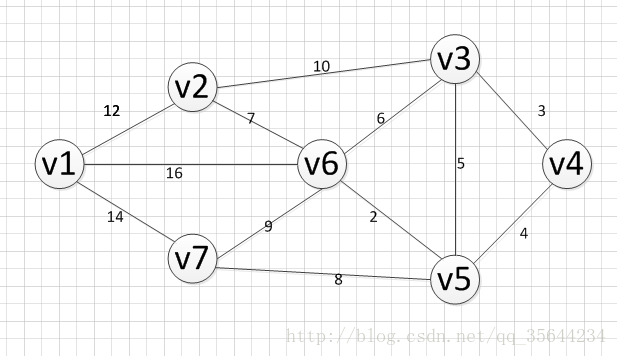
上面，我们已经介绍了算法的思路，如果，你觉得还是不理解，那么通过一个实际的例子，把算法的过程过一遍，你就明白了，如下图，我们求下图的每个点对之间的最短路径的过程如下：

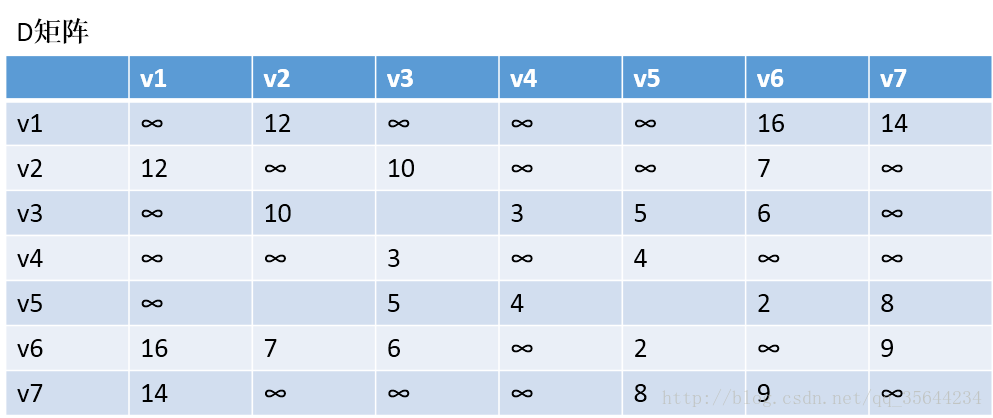
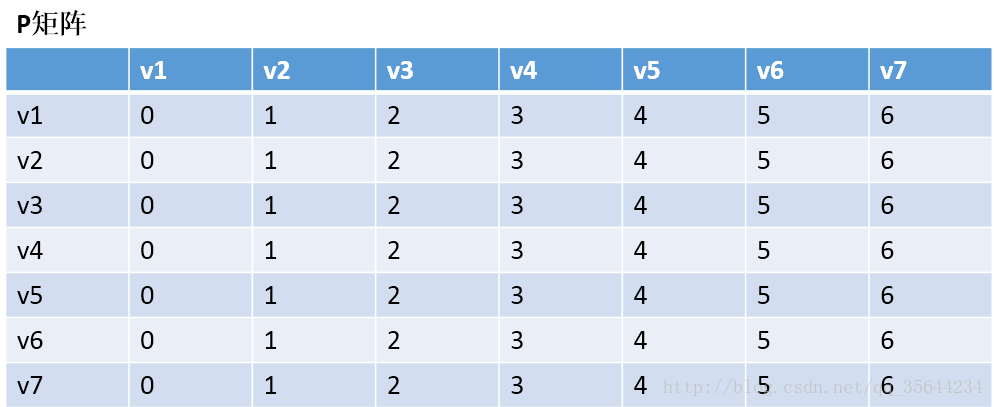
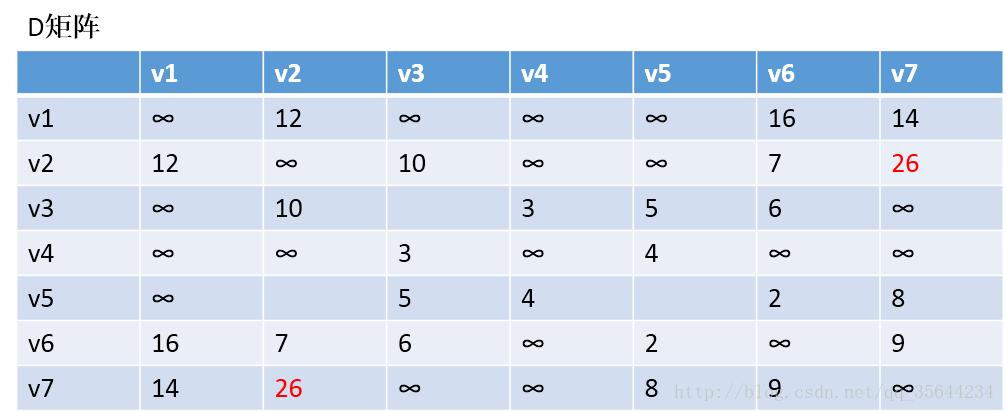
第一步，我们先初始化两个矩阵，得到下图两个矩阵： D矩阵是“邻接矩阵”

、

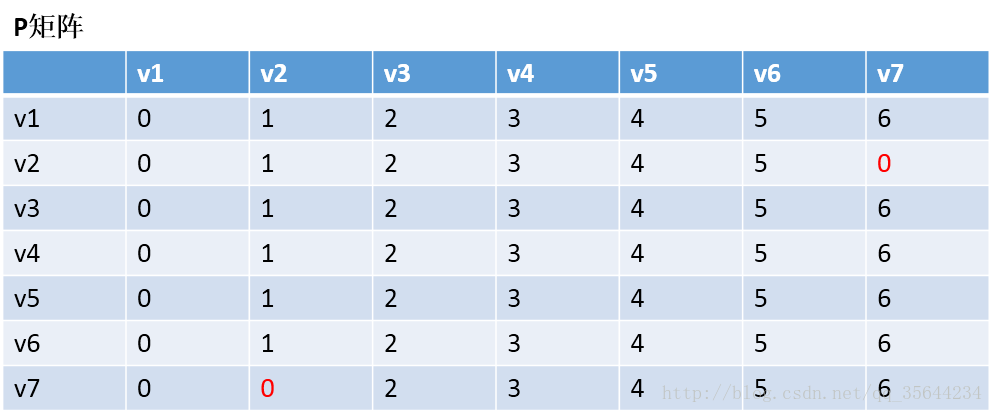
第二步，以v1为中阶，更新两个矩阵：
发现，a[1][0]+a[0][6] < a[1][6] 和a[6][0]+a[0][1] < a[6][1]，所以我们只需要矩阵D和矩阵P，结果如下：

通过矩阵P，我发现v2–v7的最短路径是：v2–v1–v7

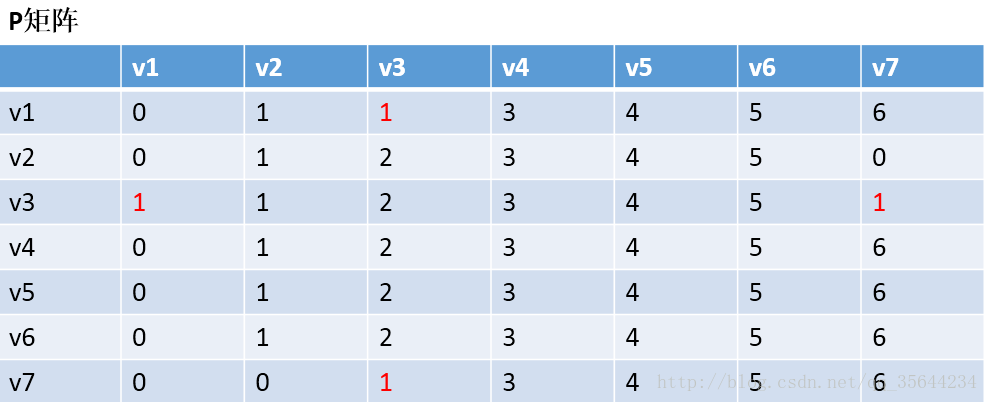
第三步：以v2作为中介，来更新我们的两个矩阵，使用同样的原理，扫描整个矩阵，得到如下图的结果：

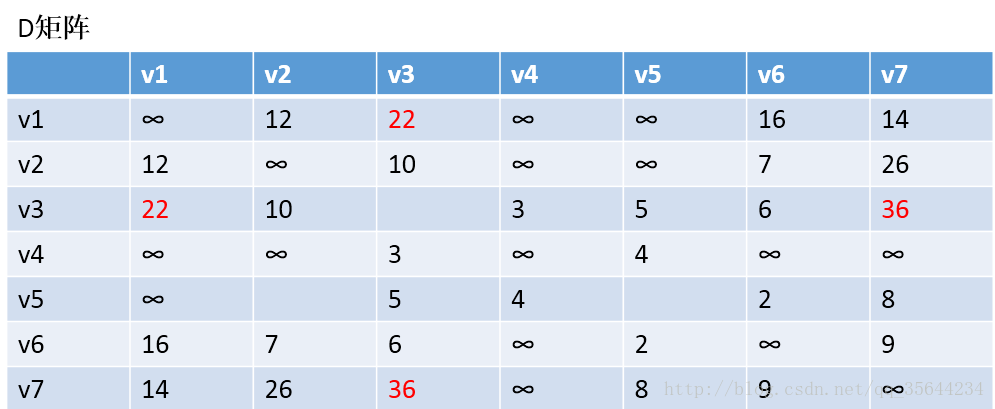
OK，到这里我们也就应该明白Floyd算法是如何工作的了，他每次都会选择一个中介点，然后，遍历整个矩阵，查找需要更新的值，下面还剩下五步，就不继续演示下去了，理解了方法，我们就可以写代码了。

public class Floyd {
    private int[][] matrix;//初始的邻接矩阵（未更新前的矩阵）
    private char[] nodes;//节点集合

    static int INF=Integer.MAX_VALUE;

    public static void main(String[] args){
        int[][] matrix={{0,5,INF},{INF,0,6},{7,9,0}};
        char[] nodes={'a','b','c'};
        Floyd floyd=new Floyd(matrix,nodes);

        //长度数组。即，dist[i][j]=sum表示，"顶点i"到"顶点j"的最短路径的长度是sum。
        int[][] distance=new int[nodes.length][nodes.length];
        //路径。path[i][j]=k表示，"顶点i"到"顶点j"的最短路径会经过顶点k。
        int[][] paths=new int[nodes.length][nodes.length];

        floyd.floydFunction(distance,paths);
    }

    public Floyd(int[][] matrix,char[] nodes){
        this.matrix=matrix;
        this.nodes=nodes;
    }

    public void floydFunction(int[][] distance,int[][] paths){
        //初始化distance[][],paths[][]
        for (int i=0;i<nodes.length;i++){
            for (int j=0;j<nodes.length;j++){
                distance[i][j]=matrix[i][j];//"顶点i"到"顶点j"的路径长度为"i到j的权值"。
                paths[i][j]=j;//"顶点i"到"顶点j"的最短路径是经过顶点j。
            }
        }
        System.out.printf("Floyd算法执行前 distance: 
");
        print(distance);
        System.out.printf("Floyd算法执行前 paths: 
");
        print(paths);

        //循环更新distance[][],paths[][]
        for (int k=0;k<nodes.length;k++){
            for (int i=0;i<nodes.length;i++){
                for (int j=0;j<nodes.length;j++){
                    int temp=(distance[i][k]==INF||distance[k][j]==INF)?INF:(distance[i][k]+distance[k][j]);
                    if(distance[i][j]>temp){
                        //// "i到j最短路径"对应的值设，为更小的一个(即经过k)
                        distance[i][j]=Math.min(temp,distance[i][j]);
                        // "i到j最短路径"对应的路径，经过k
                        paths[i][j]=k;
                    }
                }
            }
        }
        System.out.printf("Floyd算法执行后 distance: 
");
        print(distance);
        System.out.printf("Floyd算法执行后 paths: 
");
        print(paths);
    }
    // 打印floyd最短路径的结果
    public void print(int[][] distance){
        for (int i = 0; i < distance.length; i++) {
            for (int j = 0; j < distance.length; j++)
                System.out.printf("%2d  ", distance[i][j]);
            System.out.printf("
");
        }
    }
}

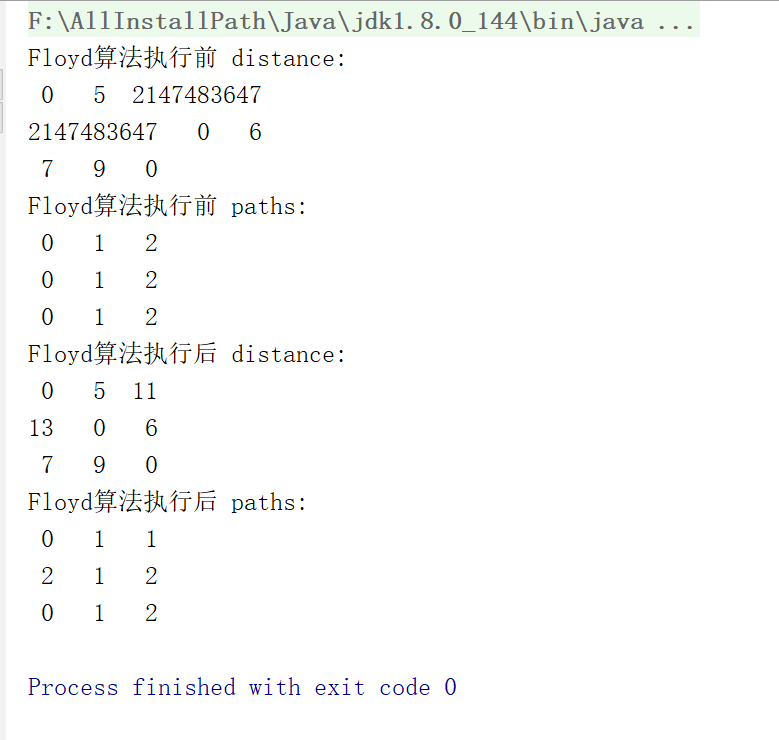
执行的结果是：