Splay,中文名称伸展树,是一种通过旋转实现平衡的二叉搜索树,由著名计算机科学家Tarjan提出来的(怎么又是你)。
首先我们需要知道二叉搜索树(Binary Search Tree,简称BST)。
二叉搜索树或者是一棵空树,或者是具有下列性质的二叉树:
1.若左子树不空,则左子树上所有结点的值均小于或等于它的根结点的值;
2.若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
2.左、右子树也分别为二叉搜索树
大致长这样:
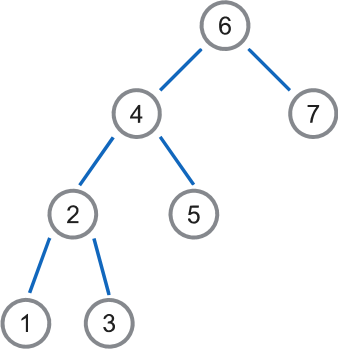
好的那我们根据这个定义,很容易发现如果我要查找树中的一个节点,需要最多O(树高)的时间复杂度,假如这棵树非常理想,左右子树大小相同,复杂度是O(logn).。但是一旦原序列是有序的,这棵树就会退化成一条链,查询的复杂度退化成O(n)。因此我们需要一种方法来使得这棵树尽可能变得“理想”,也就是做到左右子树大小差不多,达到平衡。
于是tarjan就提出了奇妙的Splay树,原理就是通过复杂度为O(logn)的splay操作调整这棵树使得它尽可能保持平衡。
首先定义一些代码中用的变量:
存树用的:
fa[N],维护一个节点的父亲的编号。
ch[N][0/1],维护一个节点的左/右儿子。
val[N],维护一个节点的点权。
cnt[N],维护一个点权重复出现的次数,这样可以减小树的规模。
siz[N],一个节点子树的大小。
好的那么我们正式开始看看一些平衡树操作:
1.id操作:确定一个点是它的父亲的左儿子还是右儿子,原理显然不赘述。
int id(int x)
{
return (ch[fa[x]][1] == x);
}
2.push_up操作:维护好节点的子树大小。注意不要忘了重复出现的(cnt[x])。
void push_up(int x)
{
siz[x] = siz[ch[x][0]] + siz[ch[x][1]] + cnt[x];
return;
}
3.rotate操作(重点!!!)
作用就是把一个节点上旋一层。
Splay旋转后,中序遍历和Splay的合法性不变。
旋转操作有四种。自行模拟后发现:
1.父节点会将连向需旋转的该子节点的方向的边连向该子节点位于其父节点方向的反方向的节点。
2.爷爷节点会将连向父节点的边连向需旋转的该节点。
3.需旋转的该节点会将连向该子节点位于其父节点方向的反方向的子节点的边连向其父节点。
void rotate(int x)
{
int y = fa[x],z = fa[y],k = id(x),w = ch[x][k ^ 1];
ch[y][k] = w;fa[w] = y;//父节点会将连向需旋转的该子节点的方向的边连向该子节点位于其父节点方向的反方向的节点。
ch[z][id(y)] = x;fa[x] = z;//爷爷节点会将连向父节点的边连向需旋转的该节点。
ch[x][k ^ 1] = y;fa[y] = x;//该节点会将连向该子节点位于其父节点方向的反方向的子节点的边连向其父节点。
push_up(x);push_up(y);
return;
}
4.find操作:将x旋转到根节点。如果x不存在,则返回x的前驱或者后继。
实现其实就是遍历一下就好。
void find(int x)
{
if(!root) return;
int now = root;
while(ch[now][x > val[now]] && x != val[now])
now = ch[now][x > val[now]];
splay(now);
return;
}
5.insert操作:插入一个数。就是通过遍历一下找到这个数应该插入的位置,如果存在这个数就++重复次数,否则新建一个节点。为了保证树仍然平衡,需要将这个节点旋转到根。
void insert(int x)
{
int now = root,p = 0;
while(now && val[now] != x)
{
p = now;
now = ch[now][x > val[now]];
}
if(now) cnt[now]++;
else
{
now = ++n;
if(p) ch[p][x > val[p]] = now;
val[now] = x;
fa[now] = p;
cnt[now] = siz[now] = 1;
}
splay(now);
return;
}
6.kth操作:查询排名为k的操作,仍然是遍历一下,如果需要到左子树去那就直接去,要到右子树去需要先算上左子树大小和根节点重复的次数,因为显然这些部分都会比右子树小,排名显然应该大于k,要处理掉。
int kth(int k)
{
int now = root;
while(1)
{
if(ch[now][0] && k <= siz[ch[now][0]]) now = ch[now][0];
else if(k > siz[ch[now][0]] + cnt[now])
{
k -= siz[ch[now][0]] + cnt[now];
now = ch[now][1];
}
else return now;
}
}
7.rank操作:查询一个数的排名,其实只要把这个数旋转到根节点统计左子树大小就能知道排名了。但是这个操作需要find支持,而如果不存在一个x能被旋转到根则会得到其前驱或后继,如果是得到后继其实也是直接统计答案,而得到前驱就需要加上根节点重复出现次数了,因为前驱显然比x小,都要算在排名里。
int rank(int x)
{
find(x);
int ans = siz[ch[root][0]];
if(val[root] < x) ans += cnt[root];
return ans;
}
8.pre和suc操作:查询一个数的前驱和后继,find一下,如果x存在,那么x就是根节点,那么它的前驱一定位于其左子树的右下角,后继一定位于其右子树的左下角,原因参见定义。而如果不存在x,得到前驱就返回前驱,得到后继就返回后继,但是如果正好相反,即得到前驱要返回后继或者得到后继要返回前驱,那其实和x存在是一样的,因为假如存在x,那么前驱和后继之间只有x,现在没有x,也就是得到的前驱的后继就是x的后继,得到的后继的前驱就是x的前驱。嗯好像有点绕qwq。
int pre(int x) //precursor
{
find(x);
if(val[root] < x) return root;
int now = ch[root][0];
while(ch[now][1]) now = ch[now][1];
return now;
}
int suc(int x) //successor
{
find(x);
if(val[root] > x) return root;
int now = ch[root][1];
while(ch[now][0]) now = ch[now][0];
return now;
}
9.del操作:删除一个节点。这个操作的实现比较巧妙,用的是上面的一个结论:x的前驱和后继之间只有x。那么我们只要把x的前驱旋转到根,再把后继旋转到右儿子处,那么得到的树中,根的左儿子只有x,这样就可以直接删除了,最后重新push_up一下就好了。
void del(int x)
{
int precursor = pre(x),successor = suc(x);
splay(precursor);
splay(successor,precursor);
int d = ch[successor][0];
if(cnt[d] > 1)
{
cnt[d]--;
splay(d);
}
else ch[successor][0] = 0;
push_up(successor),push_up(root);
return;
}
好的结合了以上的操作,我们可以成功地切掉Luogu普通平衡树的板子了。

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<ctime>
#include<cstdlib>
#include<set>
#include<queue>
#include<vector>
#include<string>
using namespace std;
#define P system("pause");
#define A(x) cout << #x << " " << (x) << endl;
#define AA(x,y) cout << #x << " " << (x) << " " << #y << " " << (y) << endl;
#define ll long long
#define inf 1000000000
#define linf 10000000000000000
#define mem(x) memset(x,0,sizeof(x))
int read()
{
int x = 0,f = 1;
char c = getchar();
while(c < '0' || c > '9')
{
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
{
x = (x << 3) + (x << 1) + c - '0';
c = getchar();
}
return f * x;
}
#define N 100010
int ch[N][2],val[N],cnt[N],fa[N],siz[N];
int root,n,q;
int id(int x)
{
return (ch[fa[x]][1] == x);
}
void push_up(int x)
{
siz[x] = siz[ch[x][0]] + siz[ch[x][1]] + cnt[x];
return;
}
void rotate(int x)
{
int y = fa[x],z = fa[y],k = id(x),w = ch[x][k ^ 1];
ch[y][k] = w;fa[w] = y;
ch[z][id(y)] = x;fa[x] = z;
ch[x][k ^ 1] = y;fa[y] = x;
push_up(x);push_up(y);
return;
}
void splay(int x,int goal = 0)
{
while(fa[x] != goal)
{
int y = fa[x],z = fa[y];
if(z != goal)
{
if(id(x) == id(y)) rotate(y);
else rotate(x);
}
rotate(x);
}
if(!goal) root = x;
return;
}
void find(int x)
{
if(!root) return;
int now = root;
while(ch[now][x > val[now]] && x != val[now])
now = ch[now][x > val[now]];
splay(now);
return;
}
void insert(int x)
{
int now = root,p = 0;
while(now && val[now] != x)
{
p = now;
now = ch[now][x > val[now]];
}
if(now) cnt[now]++;
else
{
now = ++n;
if(p) ch[p][x > val[p]] = now;
val[now] = x;
fa[now] = p;
cnt[now] = siz[now] = 1;
}
splay(now);
}
int kth(int k)
{
int now = root;
while(1)
{
if(ch[now][0] && k <= siz[ch[now][0]]) now = ch[now][0];
else if(k > siz[ch[now][0]] + cnt[now])
{
k -= siz[ch[now][0]] + cnt[now];
now = ch[now][1];
}
else return now;
}
}
int rank(int x)
{
find(x);
int ans = siz[ch[root][0]];
if(val[root] < x) ans += cnt[root];
return ans;
}
int pre(int x) //precursor
{
find(x);
if(val[root] < x) return root;
int now = ch[root][0];
while(ch[now][1]) now = ch[now][1];
return now;
}
int suc(int x) //successor
{
find(x);
if(val[root] > x) return root;
int now = ch[root][1];
while(ch[now][0]) now = ch[now][0];
return now;
}
void del(int x)
{
int precursor = pre(x),successor = suc(x);
splay(precursor);
splay(successor,precursor);
int d = ch[successor][0];
if(cnt[d] > 1)
{
cnt[d]--;
splay(d);
}
else ch[successor][0] = 0;
push_up(successor),push_up(root);
return;
}
int main()
{
q = read();
insert(-inf);
insert(inf);
while(q--)
{
int opt = read(),x = read();
switch(opt)
{
case 1:
insert(x);
break;
case 2:
del(x);
break;
case 3:
printf("%d
",rank(x));
break;
case 4:
printf("%d
",val[kth(x + 1)]);
break;
case 5:
printf("%d
",val[pre(x)]);
break;
case 6:
printf("%d
",val[suc(x)]);
break;
}
}
return 0;
}
这些只是平衡树基本操作,还有一些Splay特色操作(Splay:你才特色) ,比如区间反转,这个其实是借助打标记实现的。
首先我们需要一个push_down操作,用于下传标记,其实和线段树的差不多。
void push_down(int x)
{
if(tag[x])
{
swap(ch[x][0],ch[x][1]);//修改
tag[ch[x][0]] ^= 1;//下传
tag[ch[x][1]] ^= 1;
tag[x] = 0;//标记清空别忘了~
}
return;
}
进行区间反转的话首先我们需要找到区间,其实非常好找,比如我们需要找区间[l,r],我们只需要将排名为l-1的节点旋转到根,再将排名为r + 1的节点旋转到根节点的右儿子,那么所有排名小于l-1的数都在l-1的左子树,排名大于r+1的都在r+1的右子树,剩下的在r+1左子树的自然就是区间[l,r]的树了。由此我们就可以看出Splay区间操作多么方便了,这种提取区间显然非常好写。而在查找排名的时候要注意每访问到一个节点就要push_down一下,这一点和线段树是一样的。
int kth(int k)
{
int now = root;
while(1)
{
push_down(now);
if(ch[now][0] && k <= siz[ch[now][0]]) now = ch[now][0];
else if(k > siz[ch[now][0]] + cnt[now])
{
k -= siz[ch[now][0]] + cnt[now];
now = ch[now][1];
}
else return now;
}
}
void reverse(int l,int r)
{
int x = kth(l),y = kth(r + 2);
splay(x);
splay(y,x);
tag[ch[y][0]] ^= 1;
}
最后输出答案显然直接dfs中序遍历就好啦~
贴上Luogu文艺平衡树板子的代码:

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<ctime>
#include<cstdlib>
#include<set>
#include<queue>
#include<vector>
#include<string>
using namespace std;
#define P system("pause");
#define A(x) cout << #x << " " << (x) << endl;
#define AA(x,y) cout << #x << " " << (x) << " " << #y << " " << (y) << endl;
#define ll long long
#define inf 1000000000
#define linf 10000000000000000
#define mem(x) memset(x,0,sizeof(x))
int read()
{
int x = 0,f = 1;
char c = getchar();
while(c < '0' || c > '9')
{
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
{
x = (x << 3) + (x << 1) + c - '0';
c = getchar();
}
return f * x;
}
#define N 100010
int ch[N][2],val[N],cnt[N],fa[N],siz[N];
int root,n,ncnt,q;
int id(int x)
{
return (ch[fa[x]][1] == x);
}
void push_up(int x)
{
siz[x] = siz[ch[x][0]] + siz[ch[x][1]] + cnt[x];
return;
}
void rotate(int x)
{
int y = fa[x],z = fa[y],k = id(x),w = ch[x][k ^ 1];
ch[y][k] = w;fa[w] = y;
ch[z][id(y)] = x;fa[x] = z;
ch[x][k ^ 1] = y;fa[y] = x;
push_up(x);push_up(y);
return;
}
void splay(int x,int goal = 0)
{
while(fa[x] != goal)
{
int y = fa[x],z = fa[y];
if(z != goal)
{
if(id(x) == id(y)) rotate(y);
else rotate(x);
}
rotate(x);
}
if(!goal) root = x;
return;
}
void insert(int x)
{
int now = root,p = 0;
while(now && val[now] != x)
{
p = now;
now = ch[now][x > val[now]];
}
if(now) cnt[now]++;
else
{
now = ++ncnt;
if(p) ch[p][x > val[p]] = now;
val[now] = x;
fa[now] = p;
cnt[now] = siz[now] = 1;
}
splay(now);
}
int tag[N];
void push_down(int x)
{
if(tag[x])
{
swap(ch[x][0],ch[x][1]);
tag[ch[x][0]] ^= 1;
tag[ch[x][1]] ^= 1;
tag[x] = 0;
}
return;
}
int kth(int k)
{
int now = root;
while(1)
{
push_down(now);
if(ch[now][0] && k <= siz[ch[now][0]]) now = ch[now][0];
else if(k > siz[ch[now][0]] + cnt[now])
{
k -= siz[ch[now][0]] + cnt[now];
now = ch[now][1];
}
else return now;
}
}
void reverse(int l,int r)
{
int x = kth(l),y = kth(r + 2);
splay(x);
splay(y,x);
tag[ch[y][0]] ^= 1;
}
void dfs(int x)
{
push_down(x);
if(ch[x][0]) dfs(ch[x][0]);
if(val[x] && val[x] <= n) printf("%d ",val[x]);
if(ch[x][1]) dfs(ch[x][1]);
}
int main()
{
n = read(),q = read();
insert(0);
insert(inf);
for(int i = 1;i <= n;i++) insert(i);
while(q--)
{
int l = read(),r = read();
reverse(l,r);
}
dfs(root);
return 0;
}
看到这里的大佬们,恭喜你们学会了一个简单的数据结构,如果有锅及时评论谢谢~
