目录
- 函数调用机制分析(2018-02)
- 程序的内存区域(2018-2-07)
- 函数调用与返回的栈结构变迁图(2018-2-07)
- 函数的调用与返回本质(2018-2-07)
- 回调函数在程序设计中的应用(2018-02)
- 回调函数在C++语言中的应用(2018-2-07)
- 回调函数在C#语言中的应用(2018-2-07)
- 回调函数在JavaScript语言中的应用(2018-2-07)
- 递归函数运行机制分析(2018-02)
- 递归调用过程分析(2018-2-07)
- 利用尾递归改善递归程序的效率(2018-2-07)
- 函数的调用与返回本质(2018-2-07)
====================================================================
(一)函数调用机制分析
一个函数可以被函数调用也可以调用函数,函数调用指定了被调用函数的名字和调用函数所需要的信息(参数),程序总是从main( )函数开始启动。如图展示了典型的程序调用结构图
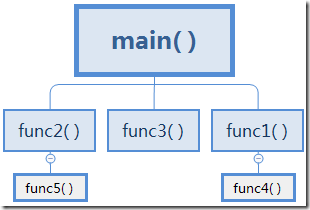
1.1)程序的内存区域
一个程序将操作系统分配给其运行的内在块分为四个区域:

1.2)函数调用与返回的栈结构变迁图


代码void main(){
int a=6,b=12;
funcA(a,b); //返回地址
}
void funcA(int aa,int bb){
int n=5
.....
funcB(n); //返回地址
}
void funcB(int s){
int x;
............
}
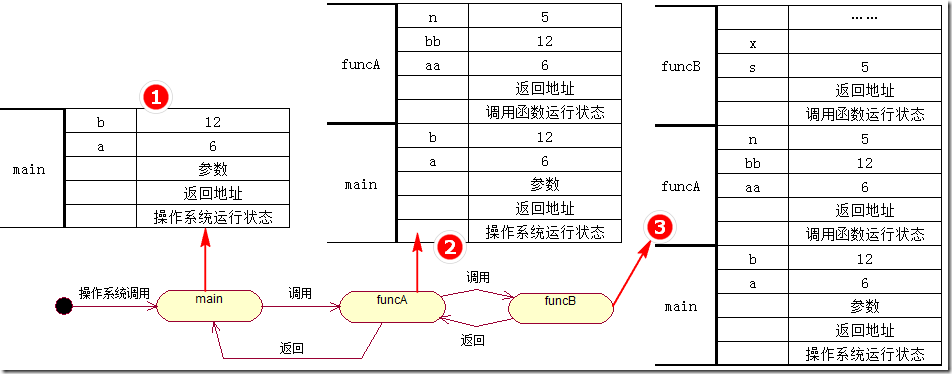
此时如果将funcB()的调用放到main()中调用则有如下状态变迁图:
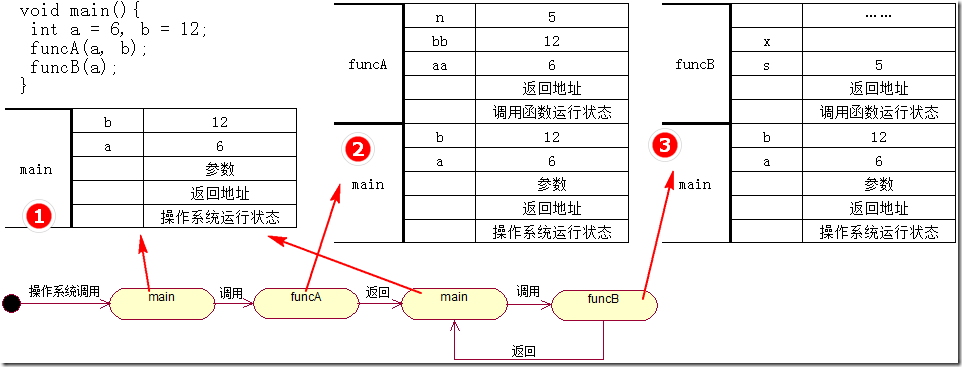
1.3)函数的调用与返回本质
将程序中的某一功能定义为一个函数后供其他函数调用才能发挥其功能。函数调用通过函数名来实现。函数完成其功能后会返回到调用点继续完成调用者的其他功能。程序在运行时会将所有的函数功能代码分配到代码区中,每个函数都有地址。本质上函数名是内存地址的一种方便人阅读和交流的表现形式。每个被调用函数都有自己的生命周期即返回到调用点继续程序的运行。既然函数名本质是一个地址值那我们可以用一个指针来表示它。如:int (*func)(int a,int b);
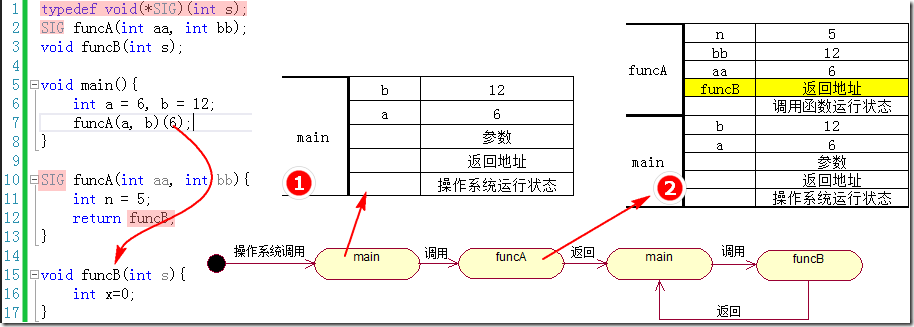
如下所示的代码描述及栈运行图分析可知:此时定义了一个函数指针作为函数参数,在调用函数时可以将被调用函数名(funcB)作为参数进行传递,有利于用户自己定义funcB函数的功能,统一的签名为func。
函数地址作为参数
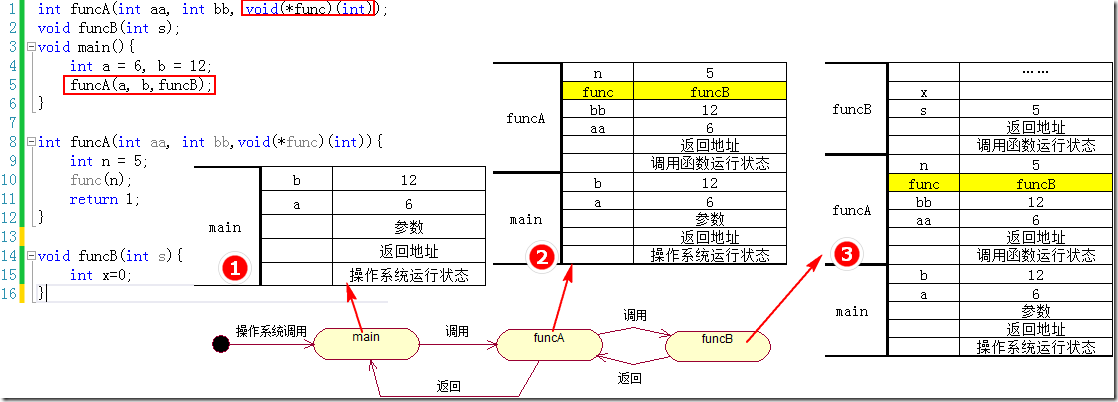
函数返回函数
(二)回调函数在程序设计中的应用
回调函数就是一个通过函数指针调用的函数。如果你把函数的指针(地址)作为参数传递给另一个函数,当这个指针被用来调用其所指向的函数时,我们就说这是回调函数。回调函数不是由该函数的实现方直接调用,而是在特定的事件或条件发生时由另外的一方调用的,用于对该事件或条件进行响应。
因为可以把调用者与被调用者分开,所以调用者不关心谁是被调用者。(类似于订阅者模式)它只需知道存在一个具有特定原型和限制条件的被调用函数。简而言之,回调函数就是允许用户把需要调用的方法的指针作为参数传递给一个函数,以便该函数在处理相似事件的时候可以灵活的使用不同的方法。 下图展示了在C++和C#回调的实现方式
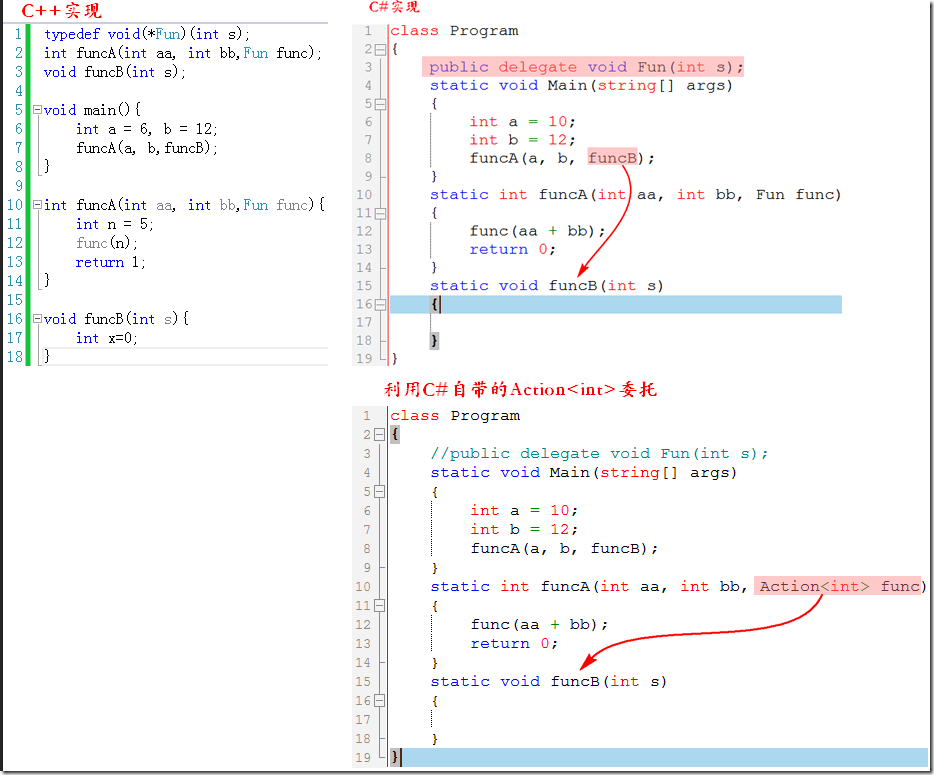
2.1)回调函数在C++语言中的应用
LRESULT CALLBACK WndProc(HWND hwnd, UINT message, WPARAM wParam, LPARAM lParam)
2.2)回调函数在C#语言中的应用
在C#语言框架中定义了几个重要的泛型委托Predicate<T>,Func<T,TResult>(有返回值的函数签名)和Action<T>(返回值为空函数签名) ,两都有如下几种具体的定义:
Predicate<T> 泛型委托
public delegate bool Predicate<T>(T obj)
Func<T,TResult>泛型委托:
public delegate TResult Func<T,TResult>(T arg)
public delegate TResult Func<T1, T2, TResult>(T1 arg1,T2 arg2)
public delegate TResult Func<T1, T2,...,TResult>(T1 arg1,T2 arg2,....)
Action<T>泛型委托:
public delegate void Action<T>(T obj)
public delegate void Action<T1, T2>(T1 arg1,T2 arg2)
public delegate void Action<T1,T2,...>(T1 arg1,T2 arg2,....)
示例分析:
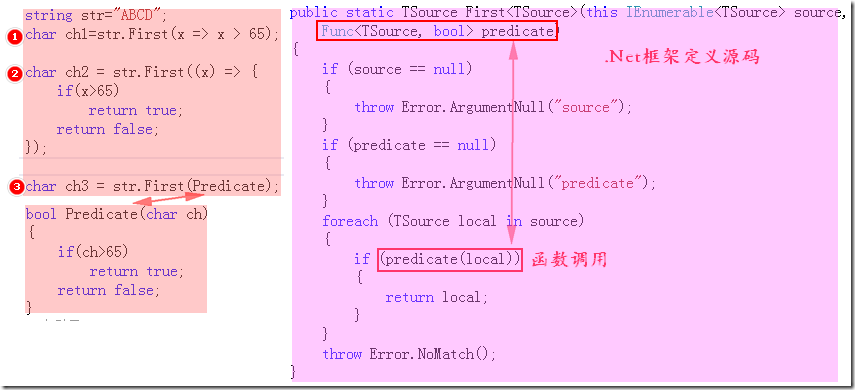
如下图标注的❶,❷,❸给出此类函数使用的三种方式。图中右半部分给出了.Net框架中关于该函数的源码定义,其本质是运用了回调函数来达到这样的目的。
方法❶:lambda表达式方式,方法❷:匿名函数(相当于C++中内联函数)方式,方法❸:回调函数方式。因此三种方式在使用上具体有等价性。都运用了Func<T,TResult>这个泛型委托。实际是在框架层面定义了一个统一回调方法。这样有利于系统框架的稳定及客户程序调用的便捷性。
Lambda表达式(lambda expression)是一个匿名函数,Lambda表达式基于数学中的λ演算得名,直接对应于其中的lambda抽象(lambda abstraction),是一个匿名函数,即没有函数名的函数。Lambda表达式可以表示闭包(注意和数学传统意义上的不同)。Lambda演算和函数式语言的计算模型天生较为接近。C#的Lambda表达式都使用Lambda 运算符 =>,分为左部,=>,右部。左部表示输入参数,右部表示需要求值的表达式(即函数返回值)。如:(x,y)=>x+y;表示该表达式的返回结果为x+y。
语法如下:形参列表=>函数体,函数体多于一条语句的可用大括号括起。
2.3)回调函数在JavaScript语言中的应用
在JavaScript语言中没有多线程的概念,所有的异步编程都用回调函数来实现。如setTimeout(fn,millisec)这样的函数都是通过传递一个函数句柄来实现异步编程。这样的函数在JS中又称为高阶函数。实际在底层实现上都是运用了函数指针的工作原理。
2.1)例子程序:假设有如下两个问题需要求解。解决方案都是对数据进行全排列后选中合适的解进行显示在控制台。但是每个问题的解满足条件不一样,这样就要求用户来自定义选出数据的函数。但是全排列的算法可以在所有类似问题复用。这样的场景就非常适合运用回调函数的方式进行处理。
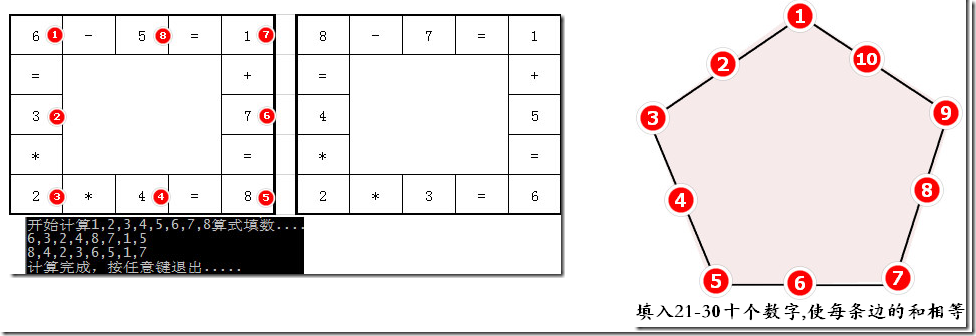


第一版代码如下using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.IO;
namespace 五边形求和
{
public static class Ext
{
static StreamWriter sw = new StreamWriter("计算.log",false,System.Text.Encoding.UTF8);
public static void Swap(int[] a, int pos, int end)
{
int temp = a[pos];
a[pos] = a[end];
a[end] = temp;
}
public static string ArrayString(int[] a)
{
//string temp = "";
StringBuilder sb = new StringBuilder();
foreach (var item in a)
{
sb.Append(item).Append(",");
}
return sb.ToString().TrimEnd(',');
}
public static void Print(string str)
{
sw.WriteLine(str);
sw.Flush();
}
public static void Dispose()
{
sw.Close();
}
}
class Program
{
private delegate void ArrayChangedEvent(string op,int[] arr);
private static ArrayChangedEvent ev = new ArrayChangedEvent(PrintResult);
private static string op = "";
private static int line = 0;
static void Main(string[] args)
{
//args=new string[]{"--five"};// args[0] = "--five";
//args = new string[] { "--eight" };// args[0] = "--five";
if (args.Length == 0)
{
Help();
Console.WriteLine("按任意键退出.....");
Console.Read();
}
if (args.Length == 1)
{
op = args[0];
switch (op)
{
case "--five":
Console.WriteLine("开始计算五边形填数....");
FiveEdge(); break;
case "--three":
Console.WriteLine("开始计算三角形填数....");
ThreeEdge();
break;
case "--start":
Console.WriteLine("开始计算星形填数....");
Start();
break;
case "--eight":
Console.WriteLine("开始计算1,2,3,4,5,6,7,8算式填数....");
Eight();
break;
default:
Console.WriteLine("没有相应计算函数,请检查");
break;
}
Ext.Dispose();
Console.WriteLine("计算完成,按任意键退出.....");
line = 0;
Console.Read();
}
}
static void Help()
{
Console.WriteLine("--five:计算五边形填数");
Console.WriteLine("--three:计算三角形填数");
Console.WriteLine("--start:计算星形填数");
Console.WriteLine("--eight:计算1,2,3,4,5,6,7,8算式填数");
}
static void FiveEdge() //计算五边形之和
{
int[] a = { 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 };
fullArray(a, 0, a.Length - 1);
}
static void ThreeEdge()
{
int[] a = { 10, 20, 30, 40, 50, 60 };
fullArray(a, 0, a.Length - 1);
}
static void Start()
{
int[] a = { 11, 12, 13, 14, 15, 16, 17, 18, 19 };
fullArray(a, 0, a.Length-1);
}
static void Eight() //填写1-8的数字算式
{
int[] a={1,2,3,4,5,6,7,8};
fullArray(a, 0, a.Length - 1);
}
private static void PrintResult(string op, int[] arr) //结果输入部分可以删除
{
switch (op)
{
case "--five":
int e1 = arr[0] + arr[1] + arr[2];
int e2 = arr[2] + arr[3] + arr[4];
int e3 = arr[4] + arr[5] + arr[6];
int e4 = arr[6] + arr[7] + arr[8];
int e5 = arr[8] + arr[9] + arr[0];
if (e1 == e2 && e2 == e3 && e3 == e4 && e4 == e5)
{
line++;
Console.WriteLine("解法" + line.ToString() + "=" + Ext.ArrayString(arr));
}
break;
case "--three":
int ee1 = arr[0] + arr[1] + arr[2];
int ee2 = arr[2] + arr[3] + arr[4];
int ee3 = arr[4] + arr[5] + arr[0];
if (ee1 == ee2 && ee2 == ee3)
{
line++;
Console.WriteLine("解法" + line.ToString() + "=" + Ext.ArrayString(arr));
}
break;
case "--start":
int x1 = arr[0] + arr[8] + arr[4];
int x2 = arr[1] + arr[8] + arr[5];
int x3 = arr[2] + arr[8] + arr[6];
int x4 = arr[3] + arr[8] + arr[7];
if (x1 == x2 && x2 == x3 && x3 == x4 && x1 == 45)
{
line++;
Console.WriteLine("解法" + line.ToString() + "=" + Ext.ArrayString(arr));
}
break;
case "--eight":
if (arr[0] - arr[7] == arr[6] && arr[0] == arr[1] * arr[2] && arr[2] * arr[3] == arr[4] && arr[4] == arr[5] + arr[6])
{
line++;
Console.WriteLine("解法" + line.ToString() + "=" + Ext.ArrayString(arr));
}
break;
default:
break;
}
}//结果输入部分可以删除
static void fullArray(int[] array, int cursor, int end) //可以加入回调方法
{
if (cursor == end)
{
Ext.Print(Ext.ArrayString(array));
ev(op, array);
}
else
{
for (int i = cursor; i <= end; i++)
{
Ext.Swap(array, cursor, i);
fullArray(array, cursor + 1, end); //可以加入回调方法
Ext.Swap(array, cursor, i); ; // 用于对之前交换过的数据进行还原
}
}
}
}
}


第二版代码如下:加入回调代码using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.IO;
namespace 五边形求和
{
public static class Ext
{
static StreamWriter sw = new StreamWriter("计算.log",false,System.Text.Encoding.UTF8);
public static void Swap(int[] a, int pos, int end)
{
int temp = a[pos];
a[pos] = a[end];
a[end] = temp;
}
public static string ArrayString(int[] a)
{
//string temp = "";
StringBuilder sb = new StringBuilder();
foreach (var item in a)
{
sb.Append(item).Append(",");
}
return sb.ToString().TrimEnd(',');
}
public static void Print(string str)
{
sw.WriteLine(str);
sw.Flush();
}
public static void Dispose()
{
sw.Close();
}
}
class Program
{
private static int line = 0;
static void Main(string[] args)
{
//args=new string[]{"--five"};// args[0] = "--five";
//args = new string[] { "--eight" };// args[0] = "--five";
if (args.Length == 0)
{
Help();
Console.WriteLine("按任意键退出.....");
Console.Read();
}
if (args.Length == 1)
{
switch (args[0])
{
case "--five":
Console.WriteLine("开始计算五边形填数....");
FiveEdge(); break;
case "--three":
Console.WriteLine("开始计算三角形填数....");
ThreeEdge();
break;
case "--start":
Console.WriteLine("开始计算星形填数....");
Start();
break;
case "--eight":
Console.WriteLine("开始计算1,2,3,4,5,6,7,8算式填数....");
Eight();
break;
default:
Console.WriteLine("没有相应计算函数,请检查");
break;
}
Ext.Dispose();
Console.WriteLine("计算完成,按任意键退出.....");
line = 0;
Console.Read();
}
}
static void Help()
{
Console.WriteLine("--five:计算五边形填数");
Console.WriteLine("--three:计算三角形填数");
Console.WriteLine("--start:计算星形填数");
Console.WriteLine("--eight:计算1,2,3,4,5,6,7,8算式填数");
}
static void FiveEdge() //计算五边形之和
{
int[] a = { 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 };
fullArray(a, 0, a.Length - 1, (arr) => {
int e1 = arr[0] + arr[1] + arr[2];
int e2 = arr[2] + arr[3] + arr[4];
int e3 = arr[4] + arr[5] + arr[6];
int e4 = arr[6] + arr[7] + arr[8];
int e5 = arr[8] + arr[9] + arr[0];
if (e1 == e2 && e2 == e3 && e3 == e4 && e4 == e5)
{
line++;
Console.WriteLine("解法" + line.ToString() + "=" + Ext.ArrayString(arr));
}
});
}
static void ThreeEdge()
{
int[] a = { 10, 20, 30, 40, 50, 60 };
fullArray(a, 0, a.Length - 1, (arr) => {
int e1 = arr[0] + arr[1] + arr[2];
int e2 = arr[2] + arr[3] + arr[4];
int e3 = arr[4] + arr[5] + arr[0];
if (e1 == e2 && e2 == e3)
{
line++;
Console.WriteLine("解法" + line.ToString() + "=" + Ext.ArrayString(arr));
}
});
}
static void Start()
{
int[] a = { 11, 12, 13, 14, 15, 16, 17, 18, 19 };
fullArray(a, 0, a.Length - 1, (arr) => {
int e1 = arr[0] + arr[8] + arr[4];
int e2 = arr[1] + arr[8] + arr[5];
int e3 = arr[2] + arr[8] + arr[6];
int e4 = arr[3] + arr[8] + arr[7];
if (e1 == e2 && e2 == e3 && e3 == e4 && e1 == 45)
{
line++;
Console.WriteLine("解法" + line.ToString() + "=" + Ext.ArrayString(arr));
}
});
}
static void Eight() //填写1-8的数字算式
{
int[] a={1,2,3,4,5,6,7,8};
fullArray(a, 0, a.Length - 1, (arr) => {
if (arr[0] - arr[7] == arr[6] && arr[0] == arr[1] * arr[2] && arr[2] * arr[3] == arr[4] && arr[4] == arr[5] + arr[6])
{
line++;
Console.WriteLine("解法" + line.ToString() + "=" + Ext.ArrayString(arr));
}
});
}
static void fullArray(int[] array, int cursor, int end,Action<int[]> callback)
{
if (cursor == end)
{
Ext.Print(Ext.ArrayString(array));
callback(array);
}
else
{
for (int i = cursor; i <= end; i++)
{
Ext.Swap(array, cursor, i);
fullArray(array, cursor + 1, end, callback);
Ext.Swap(array, cursor, i); ; // 用于对之前交换过的数据进行还原
}
}
}
}
}
(三)递归函数运行机制分析
程序调用自身的编程技巧称为递归(recursion)。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说,递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时,递归前进;当边界条件满足时,递归返回。
3.1)递归调用过程分析
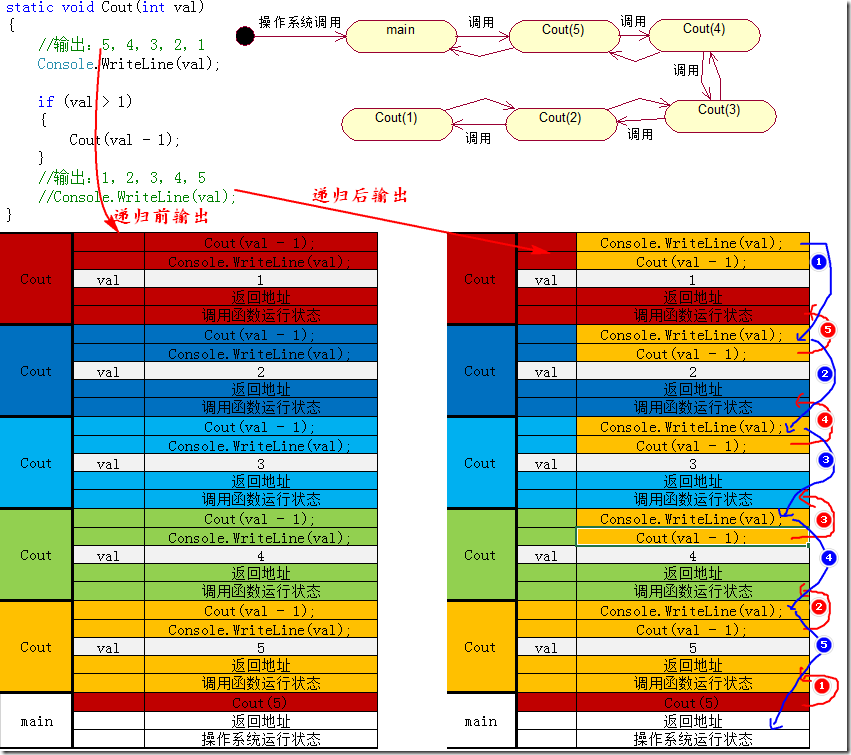
下图比较了输出语句在递归前与递归后输出结果的不同及递归栈的不同变化。
递归前输出:输出语句递归前时,函数调用时即输出值。且递归函数后面没有可以执行代码,函数直接返回。因此输出为5,4,3,2,1。
递归后输出:由于调用递归时只是入栈操作,还没有来得及执行输出语句。当前所有入栈完成后,函数调用开始返回,此时要执行输出语句后才代码一次调用返回。因此输出为:1,2,3,4,5。
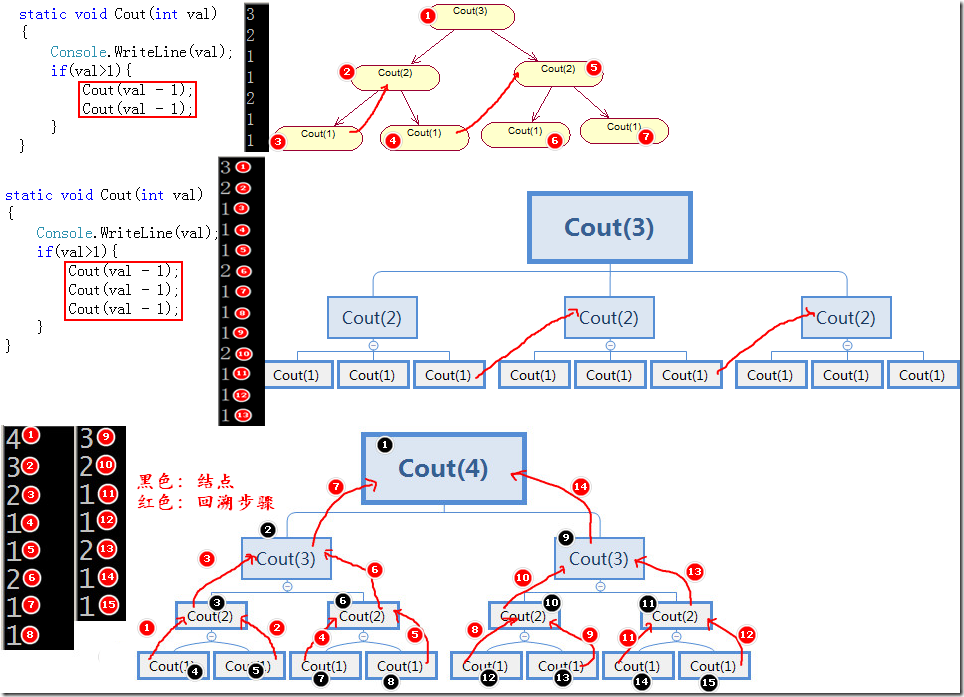
例子程序分析:如下图展示了递归树的典型过程。实际是树的先序遍历算法过程。同样也展示了多个递归函数的调用过程。
3.2)利用尾递归改善递归程序的效率










