算法导论第十二章二叉搜索树（python）

上图：

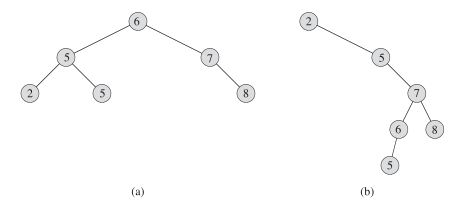
这是二叉搜索树（也有说是查找树的）基本结构：如果y是x的左子树中的一个结点，那么y.key <= x.key(如a图中的6根结点大于它左子树的每一个结点 6 >= {2,5,5}),如果y是x的右子树中的一个结点，那么y.key >x.key

注：不同堆，堆是中间的结点最大或最小，而二叉搜索树是左中右的大小顺序，我们用这个特性来遍历二叉搜索树得到是他的顺序排列（中序遍历）#中在什么地方就叫什么遍历如前序遍历：中左右后序：左右中

如图a他的中序遍历为 2->5->5->6->7->8 #从大到小

基本操作：

SEARCH：查找关键字为k的结点 O(h) #h为二叉树的高度

MINIMUM:查找二叉树的最小值（显然是最左的那个结点） O(h)

MAXIMUM:查找二叉树的最大值（显然是最右的那个结点） O(h)

PREDECESSOR:查找x的前驱y O(h)

SUCCESSOR:查找x的后驱y O(h)

INSERT:插入结点z O(h)

DELETE:删除结点z O(h)

注：

1.其中插入和删除因为要调整树的结构所以有点复杂

2.复杂都为O(h) #h为二叉树的高度,我们看下图

他们的结点数（n）都是6但是高度是不同的 ha = 2 而 hb = 4 ，这种差距在应用中可能会有很大的性能问题，同以前的快速排序一样使用随机化方法或者是其他的限定条件（如红黑树）来保证性能在一个好一点的范围内（h = logn），就是不能让二叉树保持一条直线向下

给出python实现：

  1 class Node: #结点
  2 
  3     def __init__(self,data):
  4         self.left = None
  5         self.right = None
  6         self.parent = None
  7         self.data = data
  8     def createNode(self,data):
  9         #初始化
 10         return Node(data)
 11     
 12     def inorder_tree_walk(self):
 13         """
 14         中序遍历
 15         """
 16         if self.left: #左
 17             self.left.inorder_tree_walk()
 18         print(self.data,end = ' ') #中
 19         if self.right: #右
 20             self.right.inorder_tree_walk()
 21     def tree_search(self,data):
 22         if self == None or self.data == data:
 23             return self
 24 
 25         if data < self.data:
 26             return self.left.tree_seatch(data)
 27         else :
 28             return self.right.tree_seatch(data)
 29 
 30     def iterative_tree_search(self,data):
 31         #非递归版查找一般会比递归版更快
 32         n = self
 33         while n != None and data != n.data:
 34             if data < n.data:
 35                 n = n.left
 36             else:
 37                 n = n.right
 38         return n
 39 
 40     def tree_mininum(self):
 41         if self.left:
 42             return self.left.tree_mininum()
 43         else:
 44             return self
 45 
 46     def tree_maximun(self):
 47         if self.right:
 48             return self.right.true_maximun()
 49         else:
 50             return self
 51 
 52     def tree_successor(self):
 53             
 54         """
 55         找后继：
 56         有右子树，取右子树中最小的
 57         没有右子树，也就是这个子树中最大的，应该向上找第一个把他当右子树的结点
 58         前驱 相反
 59         """
 60         x = self
 61         if x.right != None:
 62             return x.right.tree_mininum()
 63         else:
 64             p = x.parent
 65             while p and p.right == x:
 66                 x = p
 67                 p = p.parent
 68             return p
 69     def tree_predecessor(self):
 70         x = self
 71         if x.left != None:
 72             return x.left.tree_maximun()
 73         else:
 74             p = x.parent
 75             while p and p.left == x:
 76                 x = p
 77                 p = p.parent
 78             return p
 79 
 80     def tree_insert(self,data):
 81         #插入data
 82         node = self
 83         while node:
 84             if data < node.data:
 85                 next = node.left
 86             else:
 87                 next = node.right
 88             if next:
 89                 node = next
 90             else:
 91                 break
 92         nn = self.createNode(data)
 93         if data < node.data:
 94             node.left = nn
 95             node.left.parent = node
 96         else:
 97             node.right = nn
 98             node.right.parent = node
 99         return nn
100 
101     def tree_delete(self,root):
102         '''
103         1.有2子树
104             1.相对树结构移除的是self
105            
106         2.少于有2子树
107             1.相对树结点移除的是self的后继 当然删除还是self.data
108         '''
109 
110         n = self
111 
112         if n.left == None or n.right == None :
113             y = n #至多有1子树直接删除
114         else:
115             y = n.tree_successor()#要用后继覆盖他
116 
117         if y.left == None: #x 覆盖 y #至多有1个子树  y是黑的话 x的黑+1
118             x = y.right 
119         else:
120             x = y.left
121 
122         x.parent = y.parent
123         if y.parent == None:
124             root = x
125         elif y == y.parent.left:
126             y.parent.left = x
127         else:
128             y.parent.right = x
129 
130         if y != n:
131             n.data = y.data
132         return root;
133 
134 if __name__ == '__main__':
135     root = Node(6)
136     root.tree_insert(5)
137     root.tree_insert(7)
138     root.tree_insert(2)
139     root.tree_insert(3)
140     root.tree_insert(8)
141     print("中序遍历: ",end = '')
142     root.inorder_tree_walk()
143     print("
查找：",end = '')
144     test1= root.iterative_tree_search(5)
145     print(str(test1.data)+'的后继：'+str(test1.tree_successor().data))
146 
147     print("查找：",end = '')
148     test2= root.tree_search(6)
149     print(str(test2.data)+'的前驱：'+str(test2.tree_predecessor().data))
150     root = test2.tree_delete(root)
151     print("删除6后：",end = '')
152     root.inorder_tree_walk()
153     root = root.iterative_tree_search(2).tree_delete(root)
154     print("
删除2后：",end = '')
155     root.inorder_tree_walk()
156 '''
157 ================= RESTART: F:pythonalgorithms12_1_tree.py =================
158 中序遍历: 2 3 5 6 7 8 
159 查找：5的后继：6
160 查找：6的前驱：5
161 删除6后：2 3 5 7 8 
162 删除2后：3 5 7 8 
163 >>> 
164 
165 python 3.5.1 win7
166 '''

参考引用：

http://www.wutianqi.com/?cat=515&paged=4

http://blog.csdn.net/fxjtoday/article/details/6448083

相关阅读:
学生党应该去研究研究 Socket（套接字）实现原理
 收录一些硬件相关的文章
 谈谈软件开源项目
 我决定开启一个人工智能机器学习技术的普及项目 Let it Learn
我邀请民科吧网友和三江老师来反相吧辩论调和级数
 共量子论丢番图方程组数值求解最小分子解
 刚看了一下一元三次方程的解法
 研究发展 C 语言
 对量子病态定理提出的代数方程不成立的证明
 数学改革
原文地址：https://www.cnblogs.com/liguan/p/5188780.html

算法导论 第十二章 二叉搜索树（python）

算法导论第十二章二叉搜索树（python）