假定一个集合为 S={18,75,60,43,54,90,46},集合长度为n
假定选取的散列函数为:h(K)=K % m
即用元素的关键字K整除以散列表的长度m,(假定K和m均为正整数,并且m>=n),取余数作为存储该元素的散列地址。在此例中,n=7,所以假定取m=8,则得到的每个元素的散列地址为:
h(18)=18 % 13=5 h(75)=75 %13=10
h(60)=60 % 13=8 h(43)=43 %13=4
h(54)=54 % 13=2 h(90)=90 %13=12
h(46)=46 % 13=7
若根据散列地址把元素存储到散列表H[m]中,则存储映象为:
处理冲突的方法
1、开放定址法
(1) 线性探查法
向前面的例子中构造的H散列表中再插入关键字分别为31和58的两个元素,若发生冲突则使用线性探查法处理。
先看插入关键字为31的元素的情况。关键字为31的散列地址为h(31)=31 % 13=5,因H[5]单元已被占用,接着探查下一个即下标为6的单元,因该单元空闲,所以关键字为31的元素被存储到下标为6的单元中,此时对应的散列表H为:
再看插入关键字为58的元素的情况。关键字为58的散列地址为h(58)=58 % 13=6,因H[6]已被占用,接着探查下一个即下标为7的单元,因H[7]仍不为空,再接着探查下标为8的单元,这样当探查到下标为9的单元时,才查找到一个空闲单元,所以把关键字为58的元素存入该单元中,此时对应的散列表H为:
(2) 平方探查法
平方探查法的探查序列为d,d+12,d+22,…,或表示为(d+i2) % m (0≤i≤m-1)。若使用递推公式表示,则为:
d=h(K)
di=(di-1+2i-1)% m (1≤i≤m-1, d0=d)
这种方法能够较好的避免堆积现象,它的缺点是不能探查到散列表上的所有单元,但只能探查到一半单元。
(3) 双散列函数探查法
这种方法使用两个散列函数h1和h2,其中h1和前面的h(K)一样,以关键字为自变量,产生一个0至m-1之间的数作为散列地址,h2也以关键字为自变量,
产生一个1至m-1之间的,并和m互素的数作为探查序列的地址增量。
双散列函数的探查序列为:
d=h1(K)
di=(di-1+h2(K))% m (1≤i≤m-1, d0=d)
2. 链接法
链接发又称开散列法,它是把发生冲突的同义词元素用单链表链接起来的方法。
假定一个线性表B为:
B=(18,75,60,43,54,90,46,31,58,73,15,34)
为了进行散列存储,假定采用的散列函数为:
h(K)=K % 13
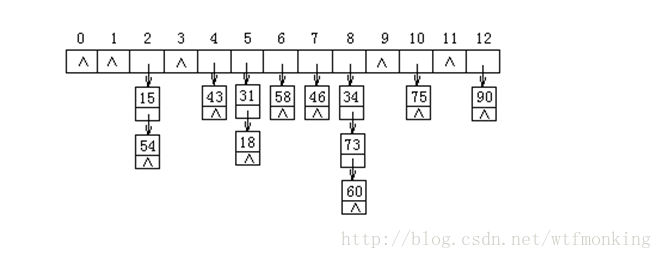
当发生冲突时,假定采用链接法处理,则得到的散列表如下图所示。
用链接法处理冲突,虽然比开放定址法多占用一些存储空间用来存储链接指针,但它可以减少在插入和查找过程中同关键字的比较次数。