A.POJ_2631


1 #include<iostream> 2 #include<cstring> 3 #include<queue> 4 #include<vector> 5 using namespace std; 6 const int maxn = 24000; 7 int vis[maxn];//把走过的点进行标记 8 int dis[maxn];//到达每个点所需要走的路径长度。 9 10 vector<pair<int, int> >A[maxn]; 11 long long ans = 0;; 12 int point = 0; 13 void bfs(int x) 14 { 15 memset(vis, 0, sizeof(vis)); 16 memset(dis, 0, sizeof(dis)); 17 queue<int> que; 18 que.push(x); 19 vis[x] = 1; 20 while (!que.empty()){ 21 int f = que.front(); 22 que.pop(); 23 if (dis[f] > ans){ 24 ans = dis[f]; 25 point = f; 26 } 27 pair<int, int> p; 28 for (int i = 0; i < A[f].size(); i++){ //开始搜索以f为起点的所有的pair 29 p = A[f][i]; //这一行是不是更能证明A[x][y]这个二维数组指向的就是一个pair; 30 if (vis[p.first] == 0){ //如果这个点没有走过则接着走。 31 vis[p.first] = 1; //标记这个点。 32 dis[p.first] = dis[f] + p.second;//p.first代表一条边的中点,p.second代表这条边的权值。 33 que.push(p.first); 34 } 35 } 36 37 } 38 } 39 int main() 40 { 41 int a, b, c; 42 while(cin >> a >> b >> c){ 43 A[a].push_back(make_pair(b, c)); 44 A[b].push_back(make_pair(a, c));//建图 45 } 46 bfs(1); 47 ans = 0; 48 bfs(point);//两次bfs求树的直径 49 cout << ans << endl; 50 return 0; 51 }
B.POJ_1849

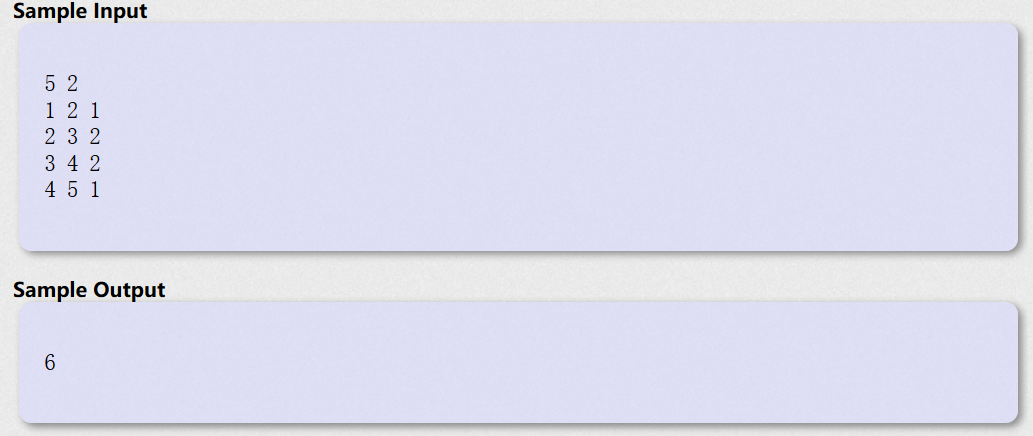
1 #include<iostream> 2 #include<cstring> 3 #include<queue> 4 #include<vector> 5 using namespace std; 6 const int maxn = 24000; 7 int vis[maxn];//把走过的点进行标记 8 int dis[maxn];//到达每个点所需要走的路径长度。 9 10 vector<pair<int, int> >A[maxn]; 11 long long ans = 0;; 12 int point = 0; 13 void bfs(int x) 14 { 15 memset(vis, 0, sizeof(vis)); 16 memset(dis, 0, sizeof(dis)); 17 queue<int> que; 18 que.push(x); 19 vis[x] = 1; 20 while (!que.empty()){ 21 int f = que.front(); 22 que.pop(); 23 if (dis[f] > ans){ 24 ans = dis[f]; 25 point = f; 26 } 27 pair<int, int> p; 28 for (int i = 0; i < A[f].size(); i++){ //开始搜索以f为起点的所有的pair 29 p = A[f][i]; //这一行是不是更能证明A[x][y]这个二维数组指向的就是一个pair; 30 if (vis[p.first] == 0){ //如果这个点没有走过则接着走。 31 vis[p.first] = 1; //标记这个点。 32 dis[p.first] = dis[f] + p.second;//p.first代表一条边的中点,p.second代表这条边的权值。 33 que.push(p.first); 34 } 35 } 36 37 } 38 } 39 int main() 40 { 41 int m, n; 42 int a, b, c; 43 int sum = 0; 44 cin >> m >> n; 45 for (int i = 0; i < m - 1; i++) { 46 cin >> a >> b >> c; 47 A[a].push_back(make_pair(b, c)); 48 A[b].push_back(make_pair(a, c));//建图 49 sum += c; 50 } 51 memset(dis, 0, sizeof(dis)); 52 memset(vis, false, sizeof(vis)); 53 bfs(1); 54 ans = 0; 55 bfs(point);//两次bfs求树的直径 56 cout << 2 * sum - ans << endl; 57 return 0; 58 }
C.找两个人开始相距最大距离除以2即为答案


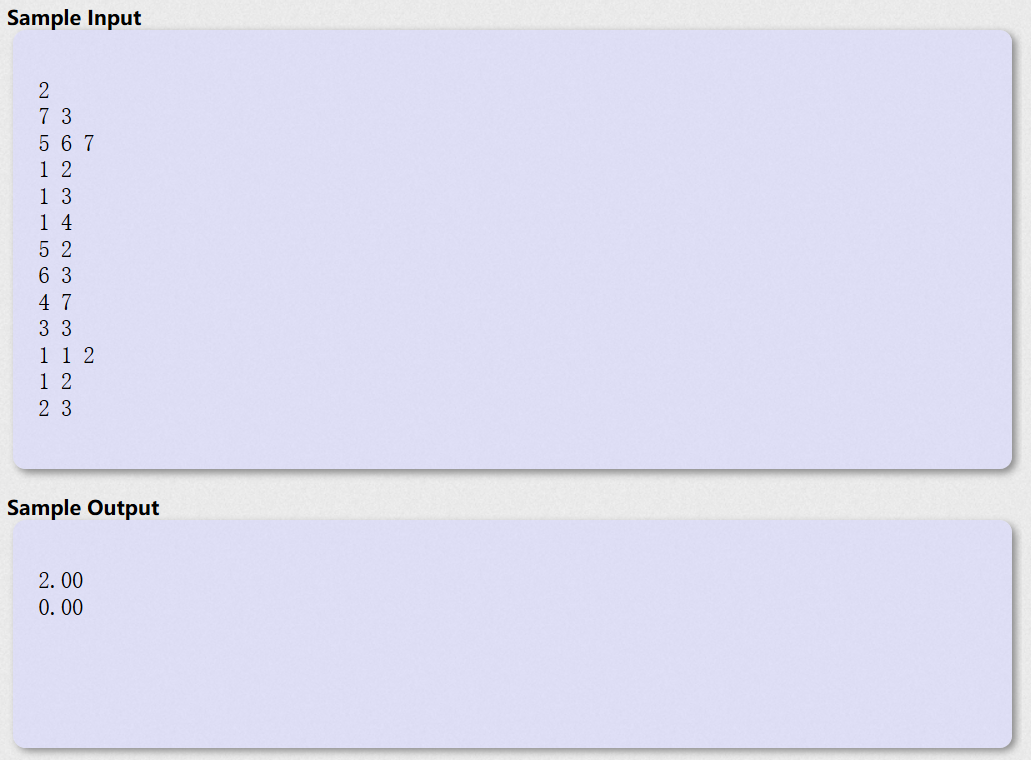
1 #include <iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<queue> 6 #include<vector> 7 #include <iomanip> 8 9 using namespace std; 10 const int MAN = 10086; 11 12 vector<int>p[MAN]; 13 int dis[MAN]; 14 int vis[MAN]; 15 int n, m, k; 16 int ans; 17 18 void dfs(int s, int num){ 19 int len = p[s].size(); 20 for (int i = 0; i < len; i++){ 21 if (!vis[p[s][i]]){ 22 vis[p[s][i]] = 1; 23 if (dis[p[s][i]] == 1) 24 ans = max(ans, num + 1); 25 dfs(p[s][i], num + 1); 26 vis[p[s][i]] = 0; 27 } 28 } 29 } 30 31 int main(){ 32 int N; 33 cin >> N; 34 while (N--){ 35 memset(dis, 0, sizeof(dis)); 36 memset(vis, 0, sizeof(vis)); 37 cin >> n >> m; 38 for (int i = 0; i <= n; i++) 39 p[i].clear(); 40 int s1 = 0, s2 = 0; 41 k = 0; 42 for (int i = 0; i < m; i++){ 43 int temp; 44 cin >> temp; 45 if (!dis[temp]) 46 k++; 47 dis[temp] = 1; 48 s1 = temp; 49 } 50 m = k; 51 for (int i = 0; i < n - 1; i++){ 52 int a, b; 53 cin >> a >> b; 54 p[a].push_back(b); 55 p[b].push_back(a); 56 } 57 if (m == 1){ 58 cout << "0.00" << endl; 59 continue; 60 } 61 queue<int>q; 62 queue<int>d; 63 int temp = 1; 64 q.push(s1); 65 d.push(0); 66 vis[s1] = 1; 67 int maxlen = 0; 68 while (!q.empty()){ 69 int s = q.front(); 70 int num = d.front(); 71 d.pop(); 72 q.pop(); 73 int len = p[s].size(); 74 for (int i = 0; i < len; i++){ 75 if (!vis[p[s][i]]) { 76 q.push(p[s][i]); 77 d.push(num + 1); 78 vis[p[s][i]] = 1; 79 if (dis[p[s][i]] == 1){ 80 temp++; 81 if (num + 1 > maxlen){ 82 maxlen = num + 1; 83 s2 = p[s][i]; 84 } 85 if (temp == m) 86 break; 87 } 88 } 89 } 90 } 91 ans = 0; 92 memset(vis, 0, sizeof(vis)); 93 vis[s2] = 1; 94 dfs(s2, 0); 95 ans /= 2; 96 double answer = ans; 97 cout << fixed << setprecision(2) << answer << endl; 98 } 99 }
D.树的内核 floyd算法(超时) 考虑用树的直径
// 超时代码
//#include<iostream>
//#include<cstring>
//#include<algorithm>
//#define FOR(a,b,c) for(int a=(b);a<(c);a++) // 利用宏定义函数简化代码
//
//using namespace std;
//
//const int maxn = 5000;
//const int INF = 1 << 30;
//int nodes[maxn], nodes_n;
//int det[maxn][maxn];
//int ans, n, S;
//
//int main() {
// ios::sync_with_stdio(false); // 提高iostream性能
// cin >> n >> S;
// FOR(i, 1, n + 1)
// FOR(j, 1, n + 1)
// if (i != j)
// det[i][j] = INF;
// int u, v, w;
// FOR(i, 0, n - 1) {
// cin >> u >> v >> w;
// det[v][u] = det[u][v] = w;
// }
// // floyd 算法
// FOR(k, 1, n + 1)
// FOR(i, 1, n + 1)
// FOR(j, 1, n + 1)
// if (det[i][k] < INF && det[k][j] < INF)
// det[i][j] = min(det[i][j], det[i][k] + det[k][j]);
// int _max = 0, maxi, maxj; //找直径
// FOR(i, 1, n + 1) FOR(j, 1, n + 1)
// if (det[i][j]<INF && det[i][j]>_max) {
// _max = det[i][j];
// maxi = i; maxj = j;
// }
// ans = INF;
// FOR(i, 1, n + 1)
// if (det[maxi][i] + det[maxj][i] == det[maxi][maxj])
// FOR(j, 1, n + 1)
// if (det[maxi][j] + det[maxj][j] == det[maxi][maxj]) {
// if (det[i][j] > S)
// continue; //直径上 长度<=S 的一段
// int ecg = max(min(det[i][maxi], det[j][maxi]), min(det[maxj][i], det[maxj][j]));
// ans = min(ans, ecg);
// }
// cout << ans << endl;
// return 0;
//}
//正解
// 两个结论
//(1)对于树中的任意一点,距离其最远的点一定是树的直径的某一端点。
//(2)所有的直径是等价的,即任意一条所能求出的该最小偏心距相等。
#include<cstdio>
#include<cstring>
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
inline const int get() {
int x = 0, f = 1;
char ch = getchar();
while (ch > '9' || ch < '0'){
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0'&&ch <= '9') {
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
const int N = 5e5 + 100;
int dis[N], f[N];
bool vis[N];
vector<pair<int, int> >det[N];
void dfs(int x) {
for (int i = 0; i < det[x].size(); i++) {
int nx = det[x][i].first;
if (vis[nx] || nx == f[x])
continue;
f[nx] = x;
dis[nx] = dis[x] + det[x][i].second;
dfs(nx);
}
}
int main() {
int n = get(), s = get();
for (int i = 1; i < n; i++) {
int u = get(), v = get(), w = get();
det[u].push_back(make_pair(v, w));
det[v].push_back(make_pair(u, w));
}
int l = 1, l2 = 1;
dis[l] = 0; dfs(l);
memset(f, 0, sizeof f);
for (int i = 1; i <= n; i++)
if (dis[i] > dis[l]) l = i;
dis[l] = 0; dfs(l);
for (int i = 1; i <= n; i++)
if (dis[i] > dis[l2])
l2 = i;
int ans = 0x7fffffff, j = l2;
for (int i = l2; i; i = f[i]) {
while (f[j] && dis[i] - dis[f[j]] <= s)
j = f[j];
ans = min(ans, max(dis[j], dis[l2] - dis[i]));
}
for (int i = l2; i; i = f[i])
vis[i] = 1;
for (int i = l2; i; i = f[i])
dis[i] = 0, dfs(i);
for (int i = 1; i <= n; i++)
ans = max(ans, dis[i]);
cout << ans << endl;
return 0;
}