一,01背包
最简单也是最经典的背包问题。
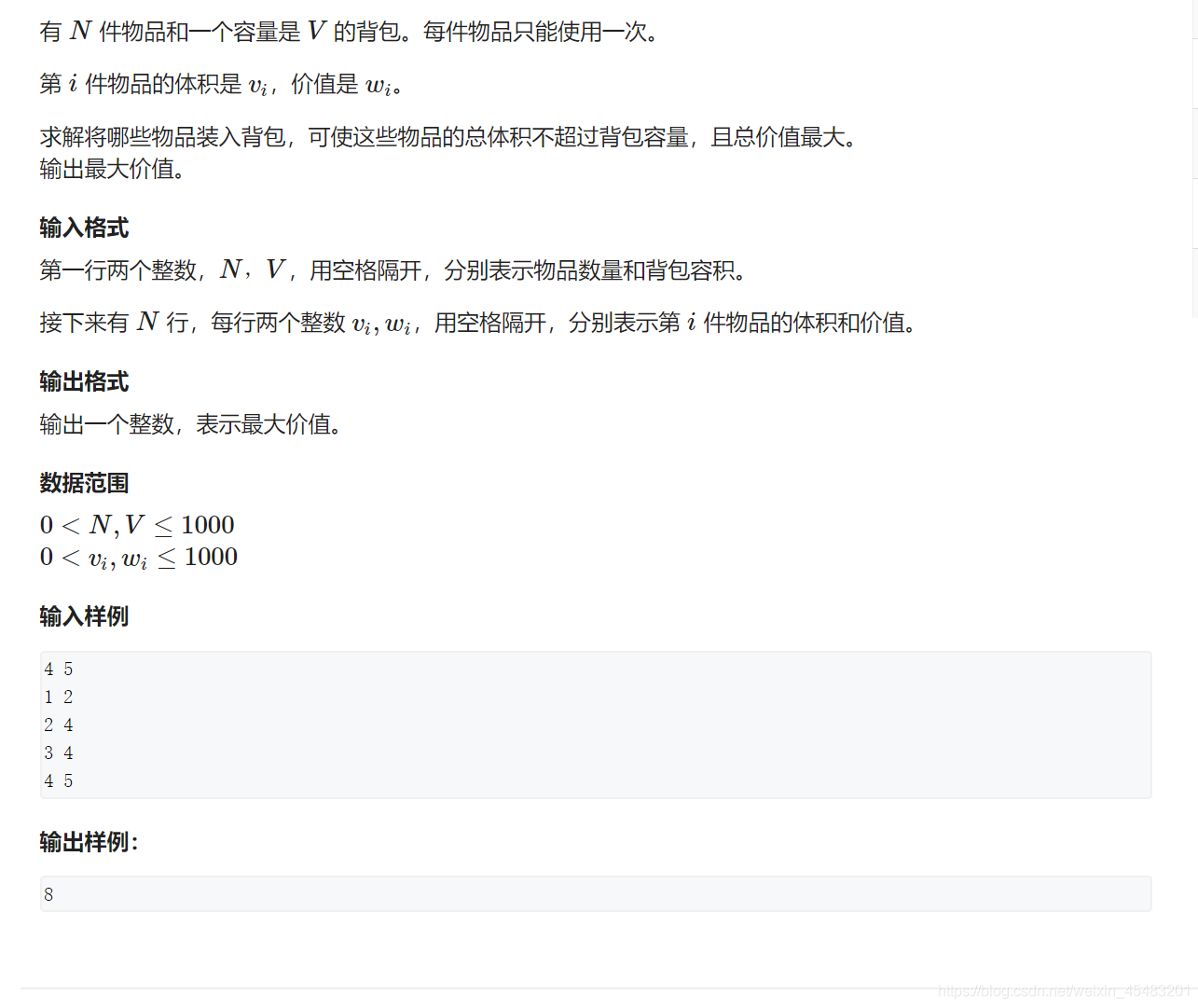
首先我们知道背包问题是一种d问题,最重要的就是要去找到他的状态转移方程。而在01背包中转移方程就比较简单了,这里用一个二维数组进行标表示。
ans[i][j]=max(ans[i-1][j],ans[i-1][j-v[i]+w[i]);
在这里i表示的是第几件物品,j表示的是背包当前课装下的最大体积,
0 1 就是有两种选择:
不装第i件物品,此时的状态就是,装上一件物品的相同体积的状态。
装第i件物品,此时还要考虑当前的背包容量能不能装得下,如果可以,就装下,此时的价值变成了,ans[i-1][j-v[i]]+w[i],
因为我们要的是在背包中尽可能的装入跟多的价值,所以这里就要取一个max值
//没有任何优化的版本。
#include<iostream>
#include<algorithm>
#include<cstring>
#define maxn 1005
int ans[maxn][maxn];
int v[maxn],w[maxn];
using namespace std;
int main() {
int n,m;
while(cin>>n>>m) {
memset(ans,0,sizeof(ans));
for(int i=1;i<=n;i++)
cin>>v[i]>>w[i];
ans[0][0]=0;
for(int i=1;i<=n;i++) {
for(int j=0;j<=m;j++) {
ans[i][j]=ans[i-1][j];
if(j>=v[i])
ans[i][j]=max(ans[i][j],ans[i-1][j-v[i]]+w[i]);
}
}
cout<<ans[n][m]<<endl;
}
return 0;
}
这是没有任何优化的版本,也是最好理解背包问题的状态转移方程的代码。
接下来我们对空间进行优化。
//空间优化版本。
#include<iostream>
#include<cstring>
#define maxn 1005
int ans[maxn];
using namespace std;
int main() {
int n,m;
while(cin>>n>>m) {
memset(ans,0,sizeof(ans));
while(n--) {
int v,w;
cin>>v>>w;
for(int i=m;i>=v;i--) {//注意在这层循环一定是从大到小,才能保证物品最多只选用一次,
ans[i]=max(ans[i],ans[i-v]+w);
}
}
cout<<ans[m]<<endl;
}
return 0;
}
二、完全背包。
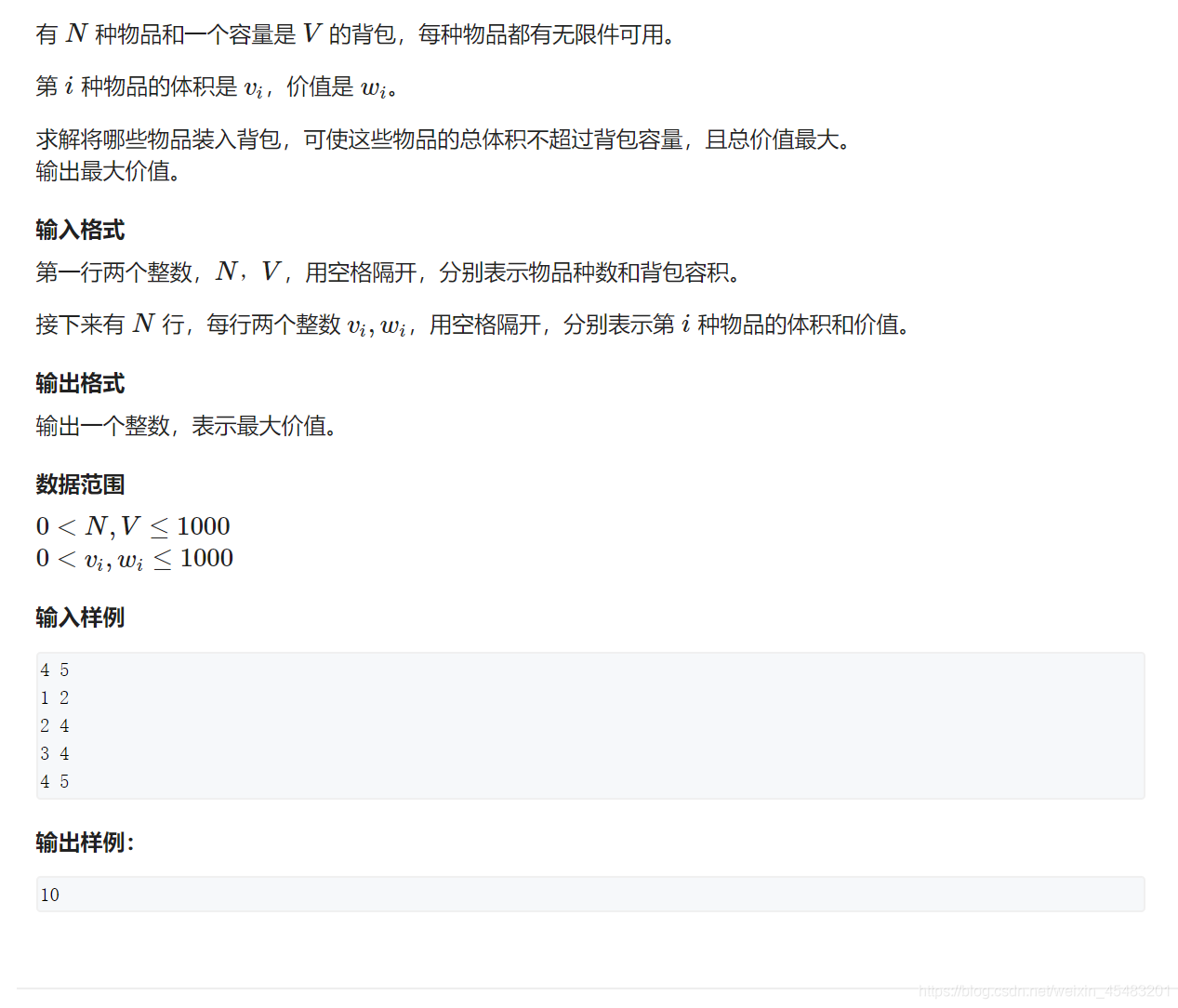
这里我们可以对上面的0 1 背包一样,对于每种可以当成是0 1背包的特殊情况,只不过每件物品是一样的。
但是在这里要注意的是,共有n次0 1背包循环,
#include<iostream>
#include<cstring>
#define maxn 1005
int ans[maxn];
using namespace std;
int main()
{
int n,m;
while(cin>>n>>m) {
memset(ans,0,sizeof(ans));
for(int i=0;i<n;i++) {
int v,w;
cin>>v>>w;
for (int j=v;j<=m;j++)//这里刚好跟上面相反,物品能多次选择
ans[j]=max(ans[j],ans[j-v]+w);
}
cout<<ans[m]<<endl;
}
return 0;
}
三、多重背包。

这一道题当我们理解了前面两道题目的是后发现并不难,只要在0 1背包加一重循环来枚举数量。
于是我们有了下面的代码。
//没有任何优化的版本。
#include<iostream>
#include<cstring>
#define maxn 1005
int ans[maxn];
using namespace std;
int main() {
int n,m;
while(cin>>n>>m) {
memset(ans,0,sizeof(ans));
while(n--) {
int v,w,s;
cin>>v>>w>>s;
for(int i=1;i<=s;i++) {
for(int j=m;j>=i*v;j--) {
ans[j]=max(ans[j],ans[j-i*v]+i*w);
}
}
}
cout<<ans[m]<<endl;
}
return 0;
}
但是我们仔细想一想,这里的时间复杂度,nVs 已经到了1e9了,这里显然会超时,想一想我们有没有什么办法来组合每一种物品的数量,
比如说15 我们可以变成,1,2,4,8的组合,而且1~15之间的任意数都可以是这几个数的组合,于是我们想到了用二进制来拆分优化数,这里的s就可以降到log2s了,
//二进制优化方法。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#define maxn 100000
int ans[maxn];
struct each {
int v,w;
};
using namespace std;
int main()
{
int n,m;
vector<each>a;
while(cin>>n>>m) {
memset(ans,0,sizeof(ans));
a.clear();
for(int i=1;i<=n;i++) {
int v1,w1,s;
cin>>v1>>w1>>s;
for(int i=1;i<=s;i*=2) {
s-=i;
a.push_back({i*v1,i*w1});
}
if(s>0)
a.push_back({s*v1,s*w1});
}
for(int i=0;i<a.size();i++) {
for(int j=m;j>=a[i].v;j--)
ans[j]=max(ans[j],ans[j-a[i].v]+a[i].w);
}
cout<<ans[m]<<endl;
}
return 0;
}
当然了对于数据没有这么大的多重背包还是可以用第一个代码来写的
其实这里还有一个单调队列优化的,但是我水平有限就,没给出代码,了,有兴趣可以自己去找一下代码,
四、混合背包。

这组样例的答案是8
其实这里就是前三种问题的汇总,我们可以在输入的时候进行处理进行分类,下面是汇总了目前我会的上面的几种方法的最优解
//二进制优化版本,加多混合背包。
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#define maxn 10005
int ans[maxn];
using namespace std;
struct each {
int v,w;
};
int main() {
int n,m;
vector<each>a;
while(cin>>n>>m) {
a.clear();
memset(ans,0,sizeof(ans));
while(n--) {
int v1,w1,s;
cin>>v1>>w1>>s;
if(s==-1) {
for(int j=m;j>=v1;j--)
ans[j]=max(ans[j],ans[j-v1]+w1);
}
else if(s==0) {
for(int j=v1;j<=m;j++)
ans[j]=max(ans[j],ans[j-v1]+w1);
}
else {
for(int i=1;i<=s;i*=2) {
s-=i;
a.push_back({i*v1,i*w1});
}
if(s>0)
a.push_back({s*v1,s*w1});
}
}
int longs=a.size();
for(int i=0;i<longs;i++)
for(int j=m;j>=a[i].v;j--)
ans[j]=max(ans[j],ans[j-a[i].v]+a[i].w);
cout<<ans[m]<<endl;
}
return 0;
}
五、分组背包。
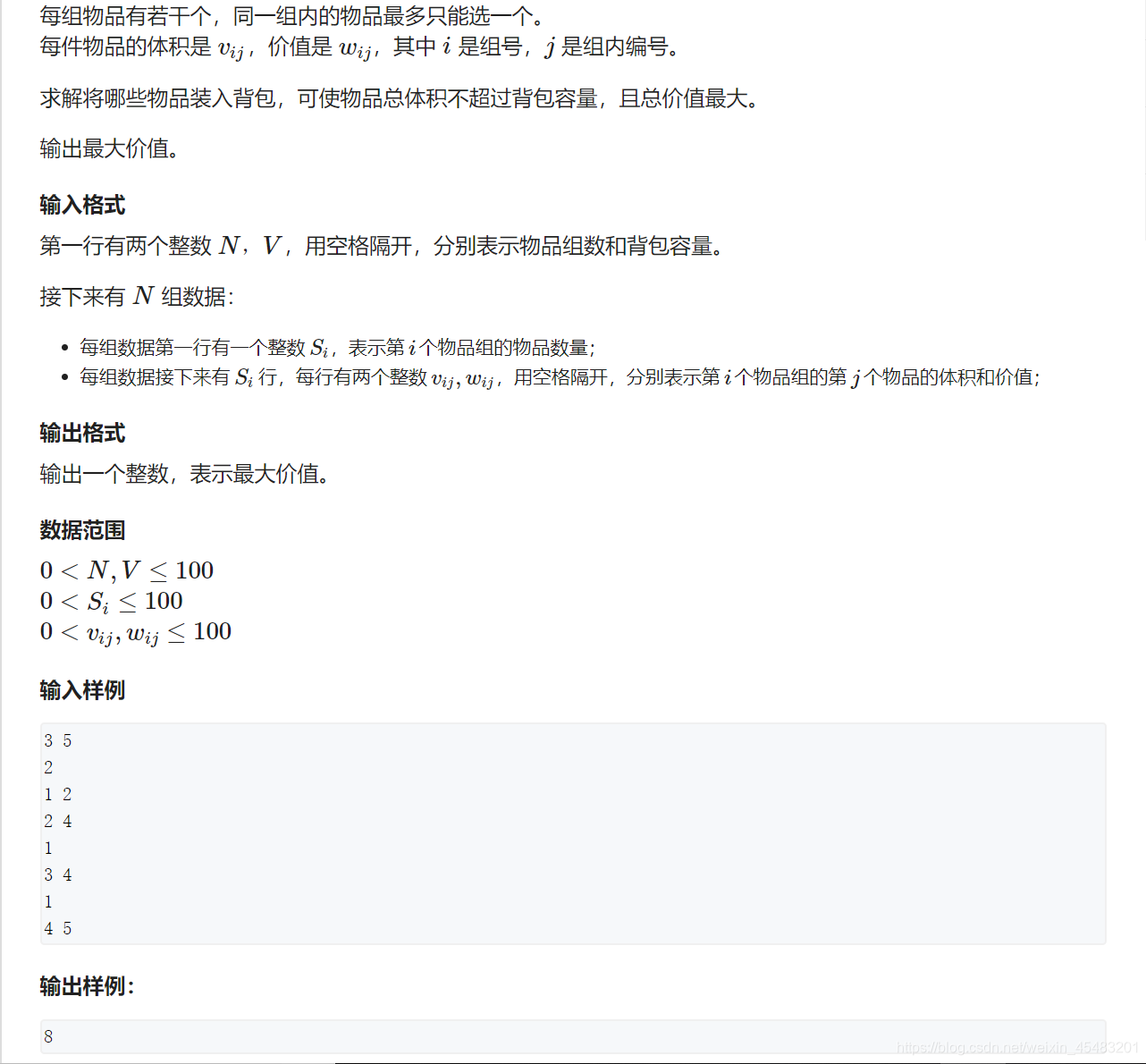
这里我们又可以吧分组背包看成是多重背包的一个特殊例子,每组个数有限制,但是只能取一个
#include<iostream>
#include<cstring>
#define maxn 105
int ans[maxn],v[maxn],w[maxn];
using namespace std;
int main() {
int n,m;
while(cin>>n>>m) {
memset(ans,0,sizeof(ans));
while(n--) {
int x;
cin>>x;
for(int i=0;i<x;i++) cin>>v[i]>>w[i];
for(int i=m;i>0;i--)
for(int j=0;j<x;j++)
if(i>=v[j]) ans[i]=max(ans[i],ans[i-v[j]]+w[j]);
}
cout<<ans[m]<<endl;
}
return 0;
}
剩下还有四个背包以后再更吧,就先写到这。