Preparing for Merge Sort
思路
手动模拟样例一后惊奇的发现了一个规律
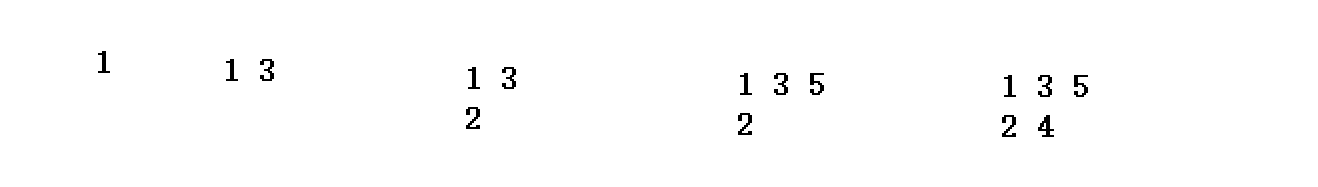
这组样例一共有两个队列输出,我们发现任意时刻每组数据都满足一个条件,最末尾的数字是严格按照单调递减的顺序的。我们每一次添加数字的操作,都是从下向上寻找最后一个小于当前要添加数字的队列编号。
这一操作是不是很像(lower\_bound - 1)的操作,但是却是一个反向的(lower\_bound - 1),于是我又开了一个数组来反向存最后一个数字,假如原本的第一组数据的最后一个数字是1,我们在下标为((n - 1))的数组上存储1,这样就可以实现我们的二分查找位置操作了。
再来说一下二分查找的细节。
假如我们的(lower\_bound)返回的是(n)下标,这说明我们没有找到比当前数字更大的数字,所以这里我们需要特判,将其添加到第一组队列数据当中去。
如果我们的(lower_bound)返回的是下标(n - 1)说明队列1末尾的最后一个数字比当前要添加的数字是更大的,所以我们需要添加到队列2当中去。
还有一点就是这里好像一定得用动态数组存答案,不然(2e5 * 2e5)会爆内存。
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
vector<int> ans[N];
int a[N], n, m, b[N];
int main() {
// freopen("in.txt", "r", stdin);
int t;
scanf("%d", &n);
for(int i = 0; i < n; i++) {
scanf("%d", &t);
int pos = lower_bound(b, b + n, t) - b;
if(pos == n) {
b[n - 1] = t;
a[0] = t;
ans[0].push_back(t);
}
else {
b[pos - 1] = t;
a[n - pos] = t;
ans[n - pos].push_back(t);
}
}
for(int i = 0; a[i]; i++) {
for(int j = 0; j < ans[i].size(); j++)
printf("%d ", ans[i][j]);
puts("");
}
return 0;
}