前言
最经想改写C用的配置读取接口, 准备采用hash或二叉树提到原先用的链表,提高查找效率.
就回顾一下二叉树,这里分享一下二叉查找树,代码很精简的, 适合学习运用二叉树查找.
需要基础
1.具备C基础知识
2.知道数据结构,最好知道一点二叉树结构
能够学到
1.稳固二叉查找树
2.C良好编码格式习惯
3.tree 数据结构几种流行套路(设计)
参照
1.二叉查找树简单分析 http://www.cppblog.com/cxiaojia/archive/2012/08/09/186752.html
(上面那个博文, 图形讲解的恨透,但是那种tree数据结构,不要参照)
正文
1 直接奔主题 说二叉查找树难点
1.1 简单说一下二叉查找树原理和突破
二叉树也是个经典的数据结构,但是工作中用的场景不多,但是我们常用过,例如map,自带排序的k-v结构.
二叉树相比双向链表在改变了插入和删除方式,使查找代价变小.因而适用领域在快速查找的领域.对于那种快速删除,
快速插入的领域并不适合.
我们今天主要回顾的是二叉查找(搜索)树. 首先看看数据结构如下
/* * 这里简单的温故一下 , 二叉查找树 *一切从简单的来吧 */ typedef int node_t; typedef struct tree { node_t v; //这里简单测试一下吧,从简单做起 struct tree* lc; struct tree* rc; } *tree_t;
上面比较简陋,不是很通用,方便了解原理设计,最后会带大家设计一些通用的二叉树结构. 这里扯一点,
结构会影响算法,算法依赖特定的结构.蛋和鸡的问题,先有一个不好的蛋,孵化一个不好的鸡,后来鸡下了很多蛋,其中一个蛋很好,
孵化了一个很好的鸡,最后蛋鸡良好循环出现了.
对于二叉查找树,除了删除比较复杂一点,其它的还是很大众的代码,这里从如何找到一个结点的父节点出发.看下面代码
/* * 查找这个结点的父结点 * root : 头结点 * v : 查找的结点 * : 返回这个v值的父亲结点,找不见返回NULL,可以返回孩子结点 */ tree_t tree_parent(tree_t root, node_t v, tree_t* pn) { tree_t p = NULL; while (root) { if (root->v == v) break; p = root; if (root->v > v) root = root->lc; else root = root->rc; } if (pn) //返回它孩子结点 *pn = root; return p; }
本质思路是,构建一个指针p保存上一个结点.这个函数相比其它函数 tree_parent 这里多返回当前的孩子结点.一个函数顺带做了两件事.
这是一个突破.推荐学习,同等代价做的事多了,价值也就提升了.
下面说一下 二叉查找树 删除原理(从上面参照文中截得,这个比较详细,但是代码写的水)
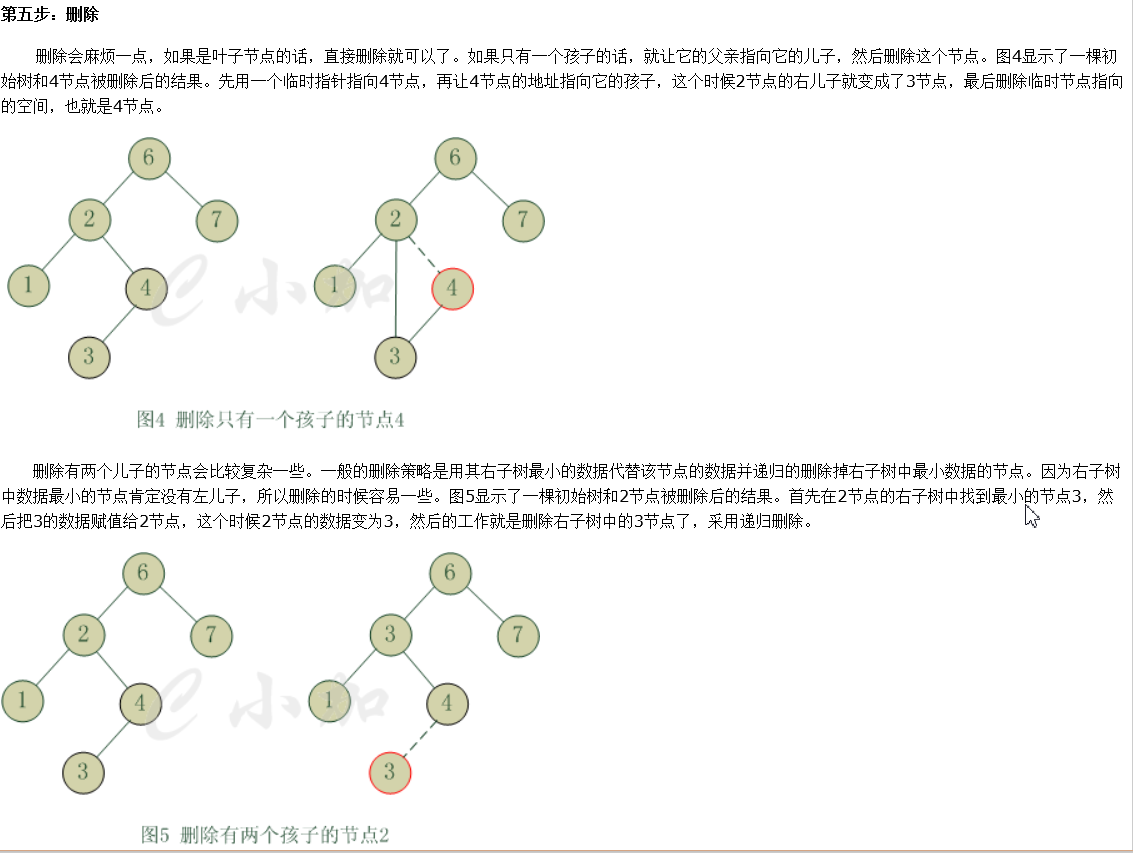
代码实现如下,有点精简,多看几遍,或者调试几遍理解更容易写.
/* * 删除结点 * proot : 指向头结点的结点 * v : 待删除的值 */ void tree_delete(tree_t* proot, node_t v) { tree_t root, n, p, t;//n表示v结点,p表示父亲结点 if ((!proot) || !(root = *proot)) return; //这里就找见 v结点 n和它的父亲结点p p = tree_parent(root, v, &n); if (!n) //第零情况 没有找见这个结点直接返回 return; //第一种情况,删除叶子结点,直接删除就可以此时t=NULL; 第二情况 只有一个叶子结点 if (!n->lc || !n->rc) { if (!(t = n->lc)) //找见当前结点n的唯一孩子结点 t = n->rc; if (!p) *proot = NULL; else { if (p->lc == n) //让当前结点的父亲收养这个它唯一的孩子 p->lc = t; else p->rc = t; } //删除当前结点并返回,C要是支持 return void; 语法就好了 free(n); return; } //第三种情况, 删除的结点有两个孩子 //将当前结点 右子树中最小值替代为它,继承王位,它没有左儿子 for (t = n->rc; t->lc; t = t->lc) ; n->v = t->v;//用nr替代n了,高效,并让n指向找到t的唯一右子树, tree_delete(&n->rc, t->v);//递归删除n右子树中最小值, 从t开始,很高效 }
第一步找见这个结点和它父亲结点,没找见它直接返回,父亲结点为了重新配置继承关系.
对于 要删除 叶子结点或只有孩子的结点, 删除 走 if(!n->lc || !n->rc) 分支不同是t
当只为叶子结点 t = NULL, 当有一个孩子结点, t = 后继结点,将其二和一了,是一个突破.
最后 删除 有两个孩子的结点, 我们的做法,将 它 右子树中最小值找到,让其替代自己, 后面在右子树中删除 那个结点.
1.2 简单扩展一下 递归的潜规则
递归大多数流程如下
//数据打印函数,全部输出,不会打印回车,中序递归 void tree_print(tree_t root) { if (root) { //简单中序找到最左结点,打印 tree_print(root->lc); printf("%d ", root->v); tree_print(root->rc); } }
这样的递归的方式 是
tree_print_0 => tree_print_1 => tree_print_2 => tree_print_3 => tree_print_2 => tree_print_1 => tree_print_0
先入函数栈后出函数栈,递归深度太长会爆栈.上面就是大多数递归的方式.
递归中有一种特殊的尾递归.不需要依赖递归返回结果.一般递归代码在函数最尾端.例如上 删除代码,结构如下
tree_delete_0 => tree_delete_0 => tree_delete_1 => tree_delete_1 => tree_delete_2 => tree_delete_2 => tree_delete_3 =>
这里代码就是入栈出栈,跳转到新的递归中.属于编译器关于递归的优化,不依赖递归返回的结果,最后一行,一般都优化为尾递归很安全.
入不同行开发,潜规则还是比较多的.扯一点, 一天晚上出租车回来和司机瞎扯淡, 他说有一天带一个导演,那个导演打电话给一个女孩父亲,
告诉他,他女儿今天晚上来他房间,痛斥一顿让她走了,后面就联系女孩父亲,女孩父亲神回复,导演你该潜你就潜. 估计当时那个导演心里就有
一万个草泥马奔过,怎么就有这么一对活宝父女.
人生活宝多才欢乐,快乐才会笑着带着'class'.
1.3 说一下接口和测试代码
一般良好安全的编程喜欢是,先写接口,再写总的测试代码,后面代码接口打桩挨个测试. 这里总的接口和测试代码如下
/* * 在二叉查找树中插入结点 * proot : 头结点的指针 * v : 待插入变量值,会自动分配内存 */ void tree_insert(tree_t* proot, node_t v); //数据打印函数,全部输出,不会打印回车,中序递归 void tree_print(tree_t root); /* * 在这个二叉查找树中查找 值为v的结点,找不见返回NULL * root : 头结点 * v : 查找结点值 * : 返回值为查找到的结点,找不见返回NULL */ tree_t tree_search(tree_t root, node_t v); /* * 查找这个结点的父结点 * root : 头结点 * v : 查找的结点 * : 返回这个v值的父亲结点,找不见返回NULL,可以返回孩子结点 */ tree_t tree_parent(tree_t root, node_t v, tree_t* pn); /* * 删除结点 * proot : 指向头结点的结点 * v : 待删除的值 */ void tree_delete(tree_t* proot, node_t v); /* * 删除这个二叉查找树,并把根结点置空 * proot : 指向根结点的指针 */ void tree_destroy(tree_t* proot); //简单输出帮助宏 #define TREE_PRINT(root) puts("当前二叉查找树的中序数据如下:"), tree_print(root), putchar(' ') //简单的主函数逻辑 int main(int argc, char* argv[]) { tree_t root = NULL; //先创建一个二叉树 试试 node_t a[] = { 8,4,5,11,2,3,7,-1,9,0,1,13,12,10 }; //中间临时变量 tree_t tmp; node_t n; int i = -1; //插入数据 while (++i<sizeof(a) / sizeof(*a)) tree_insert(&root, a[i]); //简单输出数据 TREE_PRINT(root); //这里查找数据,删除数据打印数据 n = 5; tmp = tree_search(root, n); if (tmp == NULL) printf("root is no find %d! ", n); else printf("root is find %d, is %p,%d! ", n, tmp, tmp->v); //查找父亲结点 n = 12; tmp = tree_parent(root, n, NULL); if (tmp == NULL) printf("root is no find %d! ", n); else printf("root is find parent %d, is %p,%d! ", n, tmp, tmp->v); //删除测试 n = 8; tree_delete(&root, n); TREE_PRINT(root); n = 9; tree_delete(&root, n); TREE_PRINT(root); //释放资源 tree_destroy(&root); system("pause"); return 0; }
测试代码就是把声明的接口挨个测试一遍.对于代码打桩意思就是简单的实现接口,让其能编译通过.如下
/* * 在这个二叉查找树中查找 值为v的结点,找不见返回NULL * root : 头结点 * v : 查找结点值 * : 返回值为查找到的结点,找不见返回NULL */ tree_t tree_search(tree_t root, node_t v) { return NULL; }
就是打桩. 到这里基本都万事具备了.设计思路有了,原理也明白了,下面上一个完整案例看结果.
2.汇总代码, 看运行结果
首先看运行结果截图

查找,删除,打印都来了一遍, 具体的实现代码如下
#include <stdio.h> #include <stdlib.h> #include <errno.h> #include <string.h> //控制台打印错误信息, fmt必须是双引号括起来的宏 #ifndef CERR #define CERR(fmt, ...) fprintf(stderr,"[%s:%s:%d][error %d:%s]" fmt " ", __FILE__, __func__, __LINE__, errno, strerror(errno), ##__VA_ARGS__) //检测并退出的宏 #define CERR_EXIT(fmt, ...) CERR(fmt, ##__VA_ARGS__), exit(EXIT_FAILURE) #endif/* !CERR */ /* * 这里简单的温故一下 , 二叉查找树 *一切从简单的来吧 */ typedef int node_t; typedef struct tree { node_t v; //这里简单测试一下吧,从简单做起 struct tree* lc; struct tree* rc; } *tree_t; /* * 在二叉查找树中插入结点 * proot : 头结点的指针 * v : 待插入变量值,会自动分配内存 */ void tree_insert(tree_t* proot, node_t v); //数据打印函数,全部输出,不会打印回车,中序递归 void tree_print(tree_t root); /* * 在这个二叉查找树中查找 值为v的结点,找不见返回NULL * root : 头结点 * v : 查找结点值 * : 返回值为查找到的结点,找不见返回NULL */ tree_t tree_search(tree_t root, node_t v); /* * 查找这个结点的父结点 * root : 头结点 * v : 查找的结点 * : 返回这个v值的父亲结点,找不见返回NULL,可以返回孩子结点 */ tree_t tree_parent(tree_t root, node_t v, tree_t* pn); /* * 删除结点 * proot : 指向头结点的结点 * v : 待删除的值 */ void tree_delete(tree_t* proot, node_t v); /* * 删除这个二叉查找树,并把根结点置空 * proot : 指向根结点的指针 */ void tree_destroy(tree_t* proot); //简单输出帮助宏 #define TREE_PRINT(root) puts("当前二叉查找树的中序数据如下:"), tree_print(root), putchar(' ') //简单的主函数逻辑 int main(int argc, char* argv[]) { tree_t root = NULL; //先创建一个二叉树 试试 node_t a[] = { 8,4,5,11,2,3,7,-1,9,0,1,13,12,10 }; //中间临时变量 tree_t tmp; node_t n; int i = -1; //插入数据 while (++i<sizeof(a) / sizeof(*a)) tree_insert(&root, a[i]); //简单输出数据 TREE_PRINT(root); //这里查找数据,删除数据打印数据 n = 5; tmp = tree_search(root, n); if (tmp == NULL) printf("root is no find %d! ", n); else printf("root is find %d, is %p,%d! ", n, tmp, tmp->v); //查找父亲结点 n = 12; tmp = tree_parent(root, n, NULL); if (tmp == NULL) printf("root is no find %d! ", n); else printf("root is find parent %d, is %p,%d! ", n, tmp, tmp->v); //删除测试 n = 8; tree_delete(&root, n); TREE_PRINT(root); n = 9; tree_delete(&root, n); TREE_PRINT(root); //释放资源 tree_destroy(&root); system("pause"); return 0; } /* * 在二叉查找树中插入结点 * proot : 头结点的指针 * v : 待插入变量值,会自动分配内存 */ void tree_insert(tree_t* proot, node_t v) { tree_t n, p = NULL, t = *proot; while (t) { if (t->v == v) //不让它插入重复数据 return; p = t; //记录上一个结点 t = t->v > v ? t->lc : t->rc; } //这里创建结点,创建失败直接退出C++都是这种做法 n = calloc(sizeof(struct tree), 1); if (NULL == n) CERR_EXIT("calloc struct tree error!"); n->v = v; //这里插入了,开始第一个是头结点 if (NULL == p) { *proot = n; return; } if (p->v > v) p->lc = n; else p->rc = n; } //数据打印函数,全部输出,不会打印回车,中序递归 void tree_print(tree_t root) { if (root) { //简单中序找到最左结点,打印 tree_print(root->lc); printf("%d ", root->v); tree_print(root->rc); } } /* * 在这个二叉查找树中查找 值为v的结点,找不见返回NULL * root : 头结点 * v : 查找结点值 * : 返回值为查找到的结点,找不见返回NULL */ tree_t tree_search(tree_t root, node_t v) { while (root) { if (root->v == v) return root; if (root->v > v) root = root->lc; else root = root->rc; } return NULL; } /* * 查找这个结点的父结点 * root : 头结点 * v : 查找的结点 * : 返回这个v值的父亲结点,找不见返回NULL,可以返回孩子结点 */ tree_t tree_parent(tree_t root, node_t v, tree_t* pn) { tree_t p = NULL; while (root) { if (root->v == v) break; p = root; if (root->v > v) root = root->lc; else root = root->rc; } if (pn) //返回它孩子结点 *pn = root; return p; } /* * 删除结点 * proot : 指向头结点的结点 * v : 待删除的值 */ void tree_delete(tree_t* proot, node_t v) { tree_t root, n, p, t;//n表示v结点,p表示父亲结点 if ((!proot) || !(root = *proot)) return; //这里就找见 v结点 n和它的父亲结点p p = tree_parent(root, v, &n); if (!n) //第零情况 没有找见这个结点直接返回 return; //第一种情况,删除叶子结点,直接删除就可以此时t=NULL; 第二情况 只有一个叶子结点 if (!n->lc || !n->rc) { if (!(t = n->lc)) //找见当前结点n的唯一孩子结点 t = n->rc; if (!p) *proot = t; else { if (p->lc == n) //让当前结点的父亲收养这个它唯一的孩子 p->lc = t; else p->rc = t; } //删除当前结点并返回,C要是支持 return void; 语法就好了 free(n); return; } //第三种情况, 删除的结点有两个孩子 //将当前结点 右子树中最小值替代为它,继承王位,它没有左儿子 for (t = n->rc; t->lc; t = t->lc) ; n->v = t->v;//用nr替代n了,高效,并让n指向找到t的唯一右子树, tree_delete(&n->rc, t->v);//递归删除n右子树中最小值, 从t开始,很高效 } //采用后序删除 static void __tree_destroy(tree_t root) { if (root) { __tree_destroy(root->lc); __tree_destroy(root->rc); free(root); } } /* * 删除这个二叉查找树,并把根结点置空 * proot : 指向根结点的指针 */ void tree_destroy(tree_t* proot) { if (proot) __tree_destroy(*proot); *proot = NULL; }
大家自己联系一下,代码不多,容易学习顺带回顾一下数据结构中二叉树结构,关于其中 tree_destroy 编码方式,是个人的编程习惯.
在C中变量声明后没有默认初始化, 所以习惯有这样的代码
struct sockaddr_in sddr; memset(&sddr, 0, sizeof sddr);
我觉得这样麻烦,我习惯的写法是
struct sockaddr_in saddr = { AF_INET };
利用了一个C声明初始化潜规则,上面和下面代码转成汇编后也许都相似.后面写法,默认编译器帮我们把它后面没初始化部分置成0.
还有一个习惯,可以允许一个烂的开始,必须要有一个perfect结束,参照老C++版本的智能指针,也叫破坏指针. 做法就是
char* p = malloc(1); free(p); p = NULL;
防止野指针.一种粗暴的做法,所以个人习惯在结束的时候多'浪费'一点时间回顾一下以前,再将其彻底抹除,等同于亚洲飞人直接删除所有回忆的做法.
编程的实现.最后再吐槽一下,为什么C++很烂,因为看了无数的书,还是不知道它要闹哪样.它就是一本易筋经,左练右练上练下练都可以,终于练成了
恭喜你,这张一张残废证收下.
再扯一点, 为什么C++中叫模板,上层语言中叫泛型? 哈哈,可以参照全特化和偏(范)特化.这里卖一个关子,但是本文中最后会有案例解决.
3.继往开来,了解一些数据结构设计的模式
上面基本都扯的差不多了,这里分享C中几种的数据结构设计模式.
第一种 一切解'对象'
/* * C中如何封装一个 tree '结构'(结构决定算法) */ /* * 第一种思路是 一切皆'对象' */ struct otree { void* obj; struct otree* lc; struct otree* rc; }; struct onode { int id; char* name; }; // obj => &struct onde的思路,浪费了4字节,方便管理
大家看到那个 void*应该就明白了吧等同于上层语言中Object对象.
第二种 万物皆'泛型'
/* * 第二种思路是 万物皆'泛型' */ struct tree_node { struct tree_node *lc; struct tree_node *rc; }; #define TREE_NODE struct tree_node *__tn struct ttree { TREE_NODE; //必须在第一行,不在第一行需要计算偏移量 offset //后面就是结构了 int id; char* name; };
下面这种相比上面这种节约4字节.缺点调试难.还有好多种例如模板流,特定写死流. 这里扩展一下另一个技巧
关于C中宏简化结构的代码
/* IPv6 address */ struct in6_addr { union { uint8_t __u6_addr8[16]; #if defined __USE_MISC || defined __USE_GNU uint16_t __u6_addr16[8]; uint32_t __u6_addr32[4]; #endif } __in6_u; #define s6_addr __in6_u.__u6_addr8 #if defined __USE_MISC || defined __USE_GNU # define s6_addr16 __in6_u.__u6_addr16 # define s6_addr32 __in6_u.__u6_addr32 #endif };
是不是很新奇,但是这样的代码,上层包块库都不推荐用,这些都是内核层的定义.用的越多越容易出错.
到这里基本就快结束了,上面介绍的几种结构设计思路,大家需要自己揣摩. 特别有价值.搞明白.
再扯一点,很久以前对这样的结构不明白
struct mem_storage{ union { int again; void* str; } mem; ..... };
上面again 是干什么的,后来才明白了,主要作用是设定内存对齐的字节数.方便移植.使其结构体内存结构是一样,也方便CPU读取.
思考了很多但是还不明白, 那就对了,说明你还有追求!
这里再扩展一下, 有时候
/*
常遇见下面代码
*/
void ss_free(void* arg)
{
if(....){
.....
free(arg);
return;
}
....
}
真心 希望 C中提供 return void; 语法,
这样就可以写成
return free(arg); //或者 return (void)check(arg);
这样代码会更精简, 更好看. 这里也可以通过宏设计处理
#define return_func(f, ...) f(##__VA_ARGS__); return
属于伪造吧,希望C委员会提供 return void; 语法!!
后记
错误是难免的,有问题提示马上改. 下次有机会将二叉树讲透,关于设计开发库中用的二叉树结构都来一遍,最后分享一下,实际运用的
库案例.拜~,
有时候在想如果不以经济建设为中心,是不是人会更有意思一点? 有一款小网游叫中国, 挖了无数坑,就希望大R去充值,diao丝去陪练.哈哈