同一个问题可用不同的算法解决,而一个算法的质量优劣将影响到算法乃至程序的效率,算法的复杂度分为时间复杂度和空间复杂度。(算法的复杂性体现在运行该算法时的计算机所需资源的多少上,计算机资源最重要的是时间和空间资源,因此复杂度分为时间复杂制度和空间复杂度。)
. 时间复杂度
作用:时间复杂度是度量算法执行时间的长短;(时间复杂度简单的理解就是执行语句的条数。如果有循环和递归,则忽略简单语句,直接算循环和递归的语句执行次数)
时间复杂度用大O渐进表示法表示
时间复杂度的计算:
1,找出执行语句的条数。 如果有循环和递归,则忽略简单语句,直接算循环和递归的语句执行次数;如果算法中有包含嵌套的循环,则执行次数通常是将两个循环次数相乘 ,如果算法中包含并列的循环,则将并且的相加;
2, 将语句执行次数的数量级放入大Ο记号中;
用常数1取代运行时间中的加法常数;
在修改后的运行次数函数中,只保留最高阶项;
如果最高项系数存在且不是1,则去除与这个项相乘的常数;
. 空间复杂度
作用:空间复杂度是度量算法所需存储空间的大小(算法的空间复杂度并不是计算实际占用的空间,而是计算整个算法的辅助空间单元的个数)记做S(n)=O(f(n))。
简单理解就是算法执行时创建的变量(包括临时变量)个数
①忽略常数,用O(1)表示
②递归算法的空间复杂度=递归深度N*每次递归所要的辅助空间
③对于单线程来说,递归有运行时堆栈,求的是递归最深的那一次压栈所耗费的空间的个数,因为递归最深的那一次所耗费的空间足以容纳它所有递归过程。递归是要返回上一层的,所以它所需要的空间不是一直累加起来的
普通情况下的时间复杂度和空间复杂度:
int main() { int i = 0; int j = 0; int count = 0; for (i = 0; i < n; i++) { for (j = 0; j < n; j++) { count++; } }//执行的次数是n*n for (i = 0; i < n; i++) { count++; }//执行的次数是n int sum = 10; while (sum--) { count++; }//执行的次数是10 return 0; }
语句的总执行次数:n^2+n+10
时间复杂度为 :O(n^2)
空间复杂度为:O(1)
二分查找的时间复杂度空间复杂度:
int Binary_Search(int *dest,int len, int x) { int left = 0; int right =len-1; while (left <= right) { int mid = left + (right - left) / 2; if (x == *(dest + mid)) { return mid; } else if (x < *(dest + mid)) { right = mid - 1; } else if (x > *(dest + mid)) { left = mid + 1; } }//找到返回下标,没找到返回-1 return -1; }
这里写图片描述
由上图可以得出:
在最坏的情况下,二分查找需要查找的次数为log2N次,即就是二分查找的时间复杂度为O(log2N(2为底数,N为对数))。
整个程序中所新创建变量个数为常数级的,所以空间复杂度即就是O(1)。
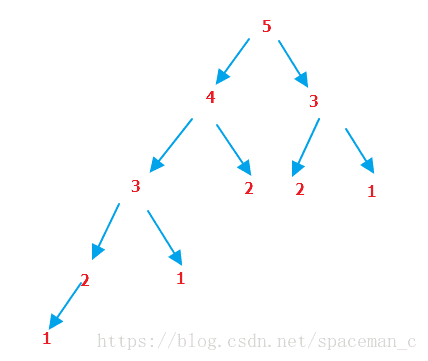
用递归实现的斐波那契数列的时间复杂度:
int fib_num(int x) { if (x < 3) return 1; else return fib_num(x - 1) + fib_num(x - 2); }
这里写图片描述
递归的总次数等于总的节点的个数2^h+1(h为层数),当求第N个斐波那契数,他递归的总次数为 2^(N-1)+1,而递归的深度为二叉树的层数 h=N-1;
斐波那契数递归算法的时间复杂度为O(2^N)
递归有运行时堆栈,求的是递归最深的那一次压栈所耗费的空间的个数,因为递归最深的那一次所耗费的空间足以容纳它所有递归过程。递归是要返回上一层的,所以它所需要的空间不是一直累加起来的
fib(5)的最深递归层数为5,fib(N)的最深递归层数为N,
空间复杂度为:O(N)
循环法求斐波那契数
int fib_iteration(int n) { int a = 1; int b = 1; int c = 1; if (n<2) { return n; } while (n>2) { c = a + b; a = b; b = c; n--; } return c; }
循环的基本次数是n-1,所用的辅助空间是3,常数级别的,所以它的时间复杂O(n)
空间复杂度:O(1)
---------------------
作者:spaceman_c
来源:CSDN
原文:https://blog.csdn.net/spaceman_c/article/details/80455561?utm_source=copy
版权声明:本文为博主原创文章,转载请附上博文链接!