影厅选座 题解

前两天我和同学们去上海的比赛做了做题（同行切磋），发现自己实力着实不够啊，人家认为难度正常的题我有一半没做出来。我先说丙组的题吧，这是最后一题，最难的一个，有好多人不会，我也算帮帮那些不会的人。

这个问题我用了一个神奇的算法——二维前缀和。这个算法和前缀和有异曲同工之妙（他俩就是差了个维度）。我们先设定a[i][j]表示前i行前j列一共有多少个空位。然后通过二位前缀和初始化，再做一些处理就好了。

要做二维前缀和，我们要理解一下原理。（下面有个拙劣的图）

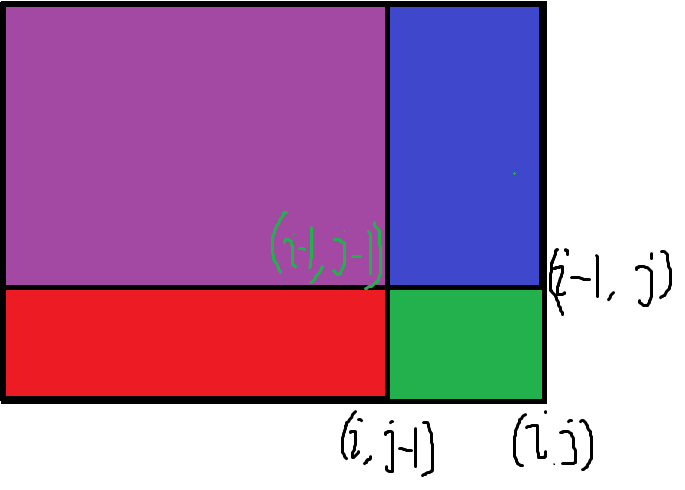
其中(i,j)就是我们要求的地方，它包含蓝色，红色，紫色，绿色。绿色是他自己所在格子，红色和紫色的和是(i,j-1)的值，蓝色和紫色的和是(i-1,j)的值。我们把他们都加起来，发现紫色算了2次，我们要把它剪掉，而紫色的部分也就是(i-1,j-1)的值，于是我们让结果减去(i-1,j-1)的值就好了。

得到公式：

a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+这一格是不是空位;

嗯，看起来不错。

经过这一系列操作，我们把数组的初始化做完了，接下来就是一些小小的优化了。

具体都写在注释里了，来看代码吧：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
long long n,m,bj,a[805][805],zshu,shu=9999999,k,hehe=0;
char sz;//我不会用scanf读入string（一直出奇怪的错误），所以这里写的是char 
long long int pd(long long int x,long long int y)
{
	for(long long int i=x;i<=n;i++)//这里应该算优化。 
	{
		for(long long int j=y;j<=m;j++) 
		{
			if(a[i][j]+a[x-1][y-1]-a[x-1][j]-a[i][y-1]>=k)
			{
				long long h=(i-x+1)*(j-y+1);
				if(h<shu)//有一个小小的知识点（对大佬来说根本算不上）if(a<b)b=a比b=min(a,b)要快。 
				{
					shu=h;
				}
			}
		}
	}
}
int main()
{
	scanf("%lld%lld%lld",&n,&m,&k);
	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<=m;j++)
		{
			scanf("%c",&sz);//scanf是一个优化的好办法，注意scanf(%c)会读入回车和空格，我们换行时要让他空读入一次。 
			bj=0;
			if(sz=='.')
			{
				bj=1;
			}
			a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+bj;//二维前缀和的公式 
		}
	}
	for(long long i=1;i<=n;i++)
	{
		for(long long j=1;j<=m;j++)
		{
			//if(a[i][j]<=shu)//一个很有用的优化，如果现在这个位置的值是小于shu的，那么也没必要截取了。
			//{
			//	continue;//（可惜我比赛的时候忘写了，写别的把他卡过去了，写上这个一定会快很多，而且这个代码的写法和那个不同，要加的话还是要改一改的） 
			//}
			pd(i,j);
		}
	}
	printf("%lld",shu);
	return 0;
}

虽然我的代码评测是过了的，但这个效率并不好，仅供大家参考。我以后会更加努力的。