要研究二叉查找树(binary search tree)首先要熟悉二叉树(binary tree)的概念与性质,二叉查找树是在二叉树基础上衍生出的数据结构。
二叉树
二叉树是一棵树,其中每个节点都不能有多于两个(<=2)的儿子。二叉树的一个性质是平均二叉树的深度要比N小得多。分析表明,这个平均深度为O(√N),而对于特殊的二叉树,即二叉查找树,其深度的平均值是O(logN)。但是二叉树的深度也是可以达到N-1的(所有的节点都在同一侧,最坏情况)。
二叉树的实现
因为二叉树中的节点最多有两个儿子,因此可以直接用指针指向它们。二叉树中的节点就是由Key(关键字)信息加上两个指向其他节点的指针(left和right)组成的结构。特别的,在插入一个节点时,必须使用malloc来创建一个节点,当删除节点时,使用free释放节点所占用的空间。具有N个节点的每一棵二叉树都将需要N+1个NULL指针。二叉树的声明如下所示:
typedef struct TreeNode *PtrToNode;
typedef struct PtrToNode Tree;
struct TreeNode
{
ElementType Element;
Tree Left;
Tree Right;
};
二叉树的应用
二叉树除了可以用于查找(主要是二叉查找树)之外,在编译器设计领域也有很重要的应用,典型的应用为处理表达式。二叉树可以用来表达一个算术表达式,称为表达式树,其中非叶节点保存操作符,叶节点保存操作数。(只考虑简单的情况,即表达式中都是二元操作的情况。)可以通过递归计算左右表达式树的值,最后将结果作用于根处的操作符上来获得整个表达式树的值。下面展示一个表达式的表达式树形式,表达式为:(a+b×(c-d))-e/f。其表示式树的形式为下图所示。
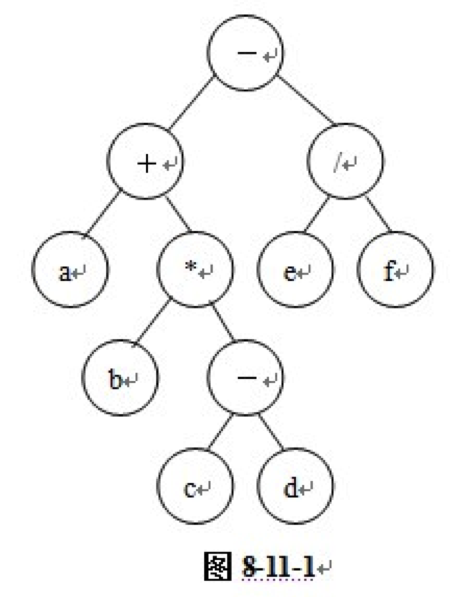
可以对此表述式树进行前缀,中缀和后缀遍历,所谓的前中后是针对操作符的输出顺序来说的,前缀遍历表示先输出操作符再输出左右子树,中缀遍历表示先输出左子树再输出操作符最后输出右子树,后缀遍历表示先输出左右子树最后输出操作符。(在非表达式树的二叉树情况下,也有前中后缀遍历,此时前中后可以理解为父节点的输出顺序。)此表达式树进行前中后缀遍历的结果分别为,
前缀:-+a*b-cd/ef
中缀:a+b*c-d-e/f
后缀:abcd-*+ef/-
其中中缀表达式为算术表达式的通常表示,只是没有括号。在计算机中后缀表达式是最方便计算的表达式形式。
可以从后缀表达式构造出一棵表示式树,算法主要借助于栈数据结构,主要思路如下:顺序读入后缀表达式的字符,当读入操作数时构造一个新的节点,并且将指向新节点的指针存放到栈中。当读入的字符为操作符时,利用操作符构造新的节点,并且从栈中弹出最上面的两棵树的指针,将操作符节点作为根,两棵子树作为根的子节点,先弹出的作为右儿子,后弹出的作为左儿子。形成新的树并将指向树的指针存入栈中,直到全部读取完表达式。最后栈中只保存一个指向最终形成的表达式树的指针。