EM算法:
让期望最大化的算法
最大似然估计:
已知:样本服从分布的模型 观测到的样本
求解:模型的参数
极大似然估计是用来估计模型参数的统计学方法 就是什么参数能使得样本符合这么一个模型
最大似然函数:什么样的参数使得出现当前这批样本概率最大 利用结果推出参数的最大值
问题提升:
有两个类别,这两个类别都服从高斯分布但是参数不同 抽取到的每个样本都不知道是从哪个分布抽取的
求解目标:男生和女生对应的高斯分布的参数
多分类的隐变量
Z=0或Z=1标记样本来自哪个分布,则Z就是隐变量
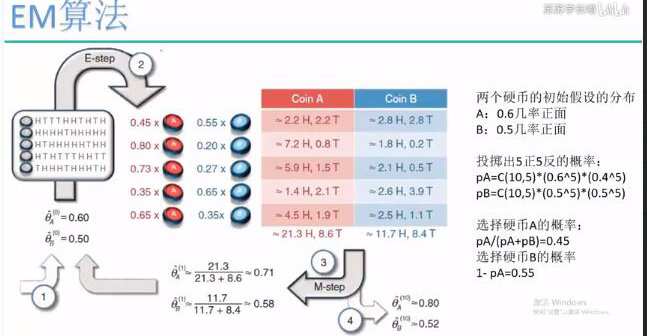
先随机初始化两个分布的参数
先知道多大概率来自不同的类 E-step
算这两种情况针对样本的情况,发生该样本情况时这两种发生该样本情况的概率。 PA=。。 PB=。。。选A的概率=PA/PA+PB PB=PB/PA+PB
算出了选择AB分别对应的概率,然后再去
A的概率乘以发生次数,这就是对应的每种硬币针对每次样本估计的结果,
对于每个样本都这么计算A和B发生的概率,然后求期望
通过每种硬币对应的期望,去更改初始设置的概率,此时的正面朝上就是正期望/正+反的期望
直到最后参数发生很小的浮动 就用EM算法算出来了最后的结果 各自分布的参数