Base64是网络上最常见的用于传输8Bit字节代码的编码方式之一,在了解Base64编码之前,先了解几个基本概念:位、字节。
位:"位(bit)"是计算机中最小的数据单位。每一位的状态只能是0或1;
字节:8个二进制位构成1个"字节(Byte)",字节是存储空间的基本计量单位。1个字节可以储存1个英文字母,2个字节可以存储1个汉字;
Base64编码的作用
因为有些网络传送渠道并不支持所有的字节,例如传统的邮件只支持可见字符的传送,像ASCII码的控制字符就不能通过邮件传送。这样就受到了很大的限制,比如图片二进制流的每个字节不可能全部是可见字符,所以就传送不了。最好的方法就是在不改变传统协议的情况下,开辟一种新的方案来支持二进制文件的传送。把不可见字符用可见字符来表示。而Base64就是一种基于64个可见字符来表示二进制数据的表示方法。
扩展:不可见字符其实并不是不显示,只是这些字符在屏幕上显示不出来,比如:换行符、回车、退格......字符。
Base64编码的原理
Base64可以将ASCII字符串或者是二进制编码成只包含A—Z,a—z,0—9,+,/ 这64个字符( 26个大写字母,26个小写字母,10个数字,1个+,一个 / 刚好64个字符)。这64个字符用6个bit位就可以全部表示出来,一个字节有8个bit 位,那么还剩下两个bit位,这两个bit位用0来补充。其实,一个Base64字符仍然是8个bit位,但是有效部分只有右边的6个 bit,左边两个永远是0。
Base64的编码规则是将3个8位字节(3×8=24位)编码成4个6位的字节(4×6=24位),之后在每个6位字节前面,补充两个0,形成4个8位字节的形式,那么取值范围就变成了0~63。又因为2的6次方等于64,所以每6个位组成一个单元。
扩展:1、为什么取值范围是0~63?
可以回顾一下二进制转换10进制的方法:
最小的二进制:00000000转换为10进制的结果是0;
最大的二进制:00111111转换为10进制的结果是:
0×27+0×26+1×25+1×24+1×23+1×22+1×21+1×20 = 63
Base64将3个字节转变为4个字节,因此,编码后的代码量(以字节为单位)约比编码前的代码量多了1/3。如果代码量正好是3的整数倍,那么恰好多了1/3。但如果不是,那么,当多出的代码量不是3的整数倍时,代码量除以3的余数就是2或者1。转换的时候,结果不够6位的用0来补上相应的位置,之后再在6位的前面补两个0。转换完空出的结果就用就用“=”来补位,总之要保证最后编码出来得字节数是4的倍数。
2、为什么要保证最后编码出来的字节数是4的倍数?
因为Base64编码时,是将3个字节转变为4个字节,最终得到的字节数必然是4的倍数
Base64编码的一个主要目的,是把任何字符都用“可视”字符表现出来。先把字符串拆开,成为六位二进制(前两位补零)的形式,这样每个字符的范围都在0-63之间了。再用BASE64的编码表,把取值范围在0-63的字符变成“可视”字符。如果不加零或只加一个零,那么取值范围就会是0-255或0-127,BASE64的编码表就要重新规定了。
扩展:为什么取值范围限制在0~63而不是0~255或者0~127?
估计可见字符有限,没有那么多的可见字符或者是Base64编码的规则、约定
下图是Base64编码对照表,数值代表字符的索引,这个是标准Base64协议规定的,不能更改。
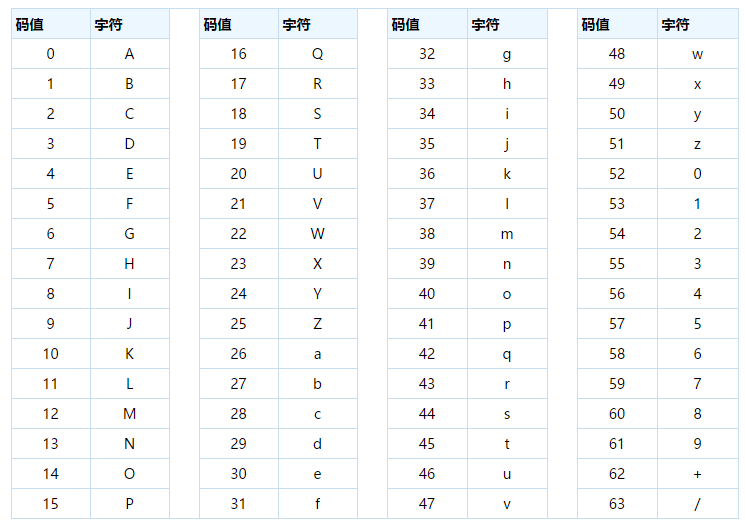
举例:
例1:
字符:SLF
对应ASCII码:S:83 L:76 F:70
转换成对应的二进制:
83:01010011、76:01001100、70:01000110
为了解释更加清晰,以下图示例:

通过Base64在线编码验证,得出结果是正确的。
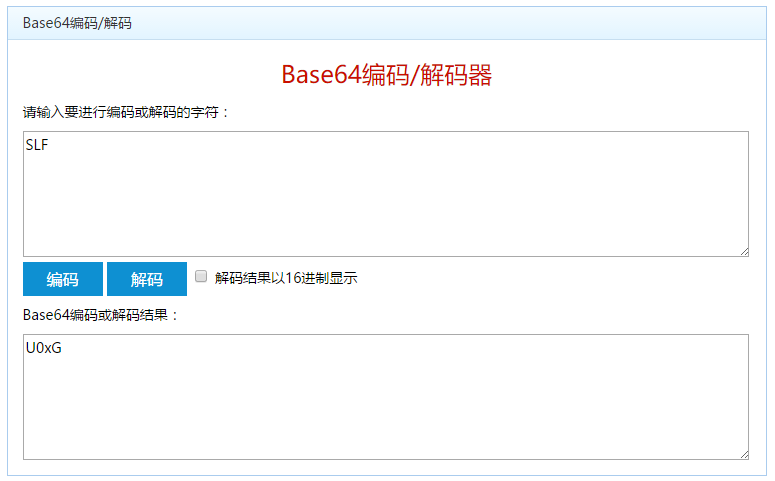
例2:
字符:M
对应ASCII码:M:77
转换成对应的二进制:
77:01001101
转换结果:

通过Base64在线编码验证,得出结果是正确的。
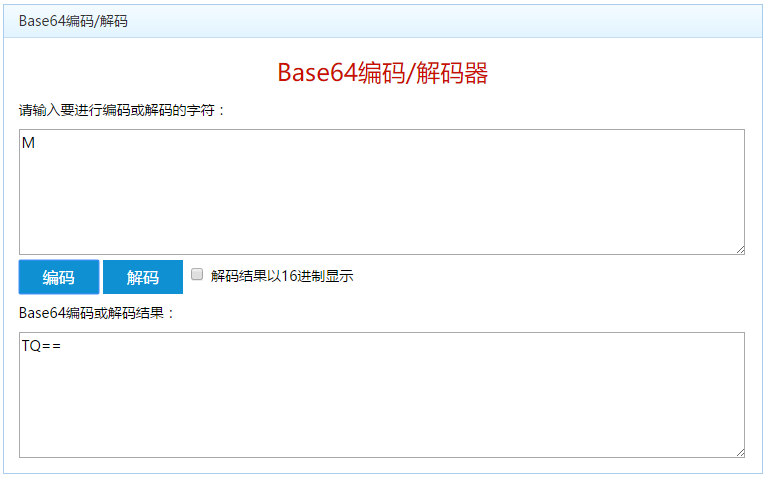
总结:Base64编码并不是真正的加密方式,它只是从二进制到字符的转换过程,说Base64编码是加密方法,只是因为经过Base64编码之后,让人一眼看上去不知道什么内容而已。