上一节分析了ArrayList,这次分析一下LinkedList,LinkedList相对我来说使用的比较少一些,一般都直接使用ArrayList,这次看源码希望自己可以把这些集合能够使用的更加适合的场景,能够根据实际情况做更多的考虑。
LinkedList概述
一看名字就知道它肯定是使用链表实现的List集合,LinkedList是基于双向链表实现的,
实现所有可选的列表操作,并允许所有元素(包括null)。注意LinkedList实现不是同步的,所以如果需要在多线程中使用它,则它必须在外部进行同步。使用这样的:
List list = Collections.synchronizedList(new LinkedList(...));
LinkedList也具有快速失败的特性,如果列表迭代器结构改性后创建的任何时间,以任何方式除了通过迭代器的删除或添加方法,迭代器将抛出一个concurrentmodificationexception。因此,面对并发修改时,迭代器会快速而干净地失败,而不是在未来的某个时间内冒任意、不确定的行为。
LinkedList源码分析
2.1、定义
public class LinkedList<E> extends AbstractSequentialList<E> implements List<E>, Deque<E>, Cloneable, java.io.Serializable
继承AbstractSequentialList,AbstractList此类提供了 List 接口的骨干实现,从而最大限度地减少了实现受“连续访问”数据存储(如链接列表)支持的此接口所需的工作。对于随机访问数据(如数组),应该优先使用 AbstractList,而不是先使用此类(百度百科)。实现了List,Deque双端队列。是一种具有队列和栈的性质的数据结构。实现了Cloneable、序列化Serializable。
2.2、属性
transient int size = 0;//大小等于0
transient Node<E> first;//指向第一个节点。
transient Node<E> last;//指向最后一个节点。
private static final long serialVersionUID = 876323262645176354L;//序列号
private static class Node<E> {//节点对象,典型的双向链表定义方式 E item;//元素 Node<E> next;//下一个节点 Node<E> prev;//上一个节点 Node(Node<E> prev, E element, Node<E> next) { this.item = element; this.next = next; this.prev = prev; } }
2.3、构造方法
public LinkedList() {//构造一个空的列表,里面什么都没有做 }
public LinkedList(Collection<? extends E> c) {////构造一个包含指定集合的元素的列表,按照它们由集合的迭代器返回的顺序。 this();//调用空的构造 addAll(c); } //按照指定集合的迭代器返回的顺序将指定集合中的所有元素追加到此列表的末尾。 如果在操作进行中修改了指定的集合,则此操作的行为是未定义的。 (注意,如果指定的集合是此列表,并且它是非空的,则会发生这种情况。) public boolean addAll(Collection<? extends E> c) { return addAll(size, c); } //将指定集合中的所有元素插入到此列表中,从指定的位置开始。 将当前位于该位置(如果有的话)的元素和随后的任何元素移动到右边(增加其索引)。 新元素将按照指定集合的迭代器返回的顺序显示在列表中。 public boolean addAll(int index, Collection<? extends E> c) { checkPositionIndex(index);//检查下标 Object[] a = c.toArray();//变为数组 int numNew = a.length;//插入的个数 if (numNew == 0)//如果为0,返回false return false; Node<E> pred, succ;//定义2个节点 if (index == size) {////获取插入位置的节点,若插入的位置在size处,则是插入到原来的后面, succ = null; pred = last; } else {//否则获取index位置处的节点,插入到他们之间 succ = node(index);//获得index下的节点 pred = succ.prev; } for (Object o : a) { @SuppressWarnings("unchecked") E e = (E) o;//把O转换为E Node<E> newNode = new Node<>(pred, e, null);//否则获取index位置处的节点 if (pred == null)//原来就是没有的情况,插入到第一个的情况 first = newNode; else//原来就是有的情况,pred = last;最后一个next挂新的节点 pred.next = newNode; pred = newNode;//pred赋值新的节点 } if (succ == null) {//插入到原来的最后面的情况 last = pred; } else {//插入到原来的中间的情况 pred.next = succ; succ.prev = pred; } size += numNew;//元素个数增加 modCount++;//操作次数增加 return true; }
Node<E> node(int index) {//返回指定元素索引处的(非空)节点。 if (index < (size >> 1)) {//小于一半就从前往后找 Node<E> x = first; for (int i = 0; i < index; i++) x = x.next; return x; } else {//大于一半就从后面找 Node<E> x = last; for (int i = size - 1; i > index; i--) x = x.prev; return x; } }
2.4、增加方法
public boolean add(E e) {//将指定的元素追加到此列表的末尾。 linkLast(e); return true; } void linkLast(E e) {//链接e作为最后一个元素。 final Node<E> l = last;//定义一个新的节点赋值为last final Node<E> newNode = new Node<>(l, e, null);//根据插入的值创建一个新节点,新节点的pre指向last,next为null last = newNode;//last节点赋值为新节点 if (l == null)//如果l为空,即里面没有节点的情况 first = newNode;第一个节点为新节点 else//LinkedList里面有节点的情况 l.next = newNode;//最后一个节点的下一个节点为新节点 size++;//列表大小加1 modCount++;//操作数增加 }
基于增加方法在1.7确实有一些难以理解,我还是简单画一个流程图来展示:
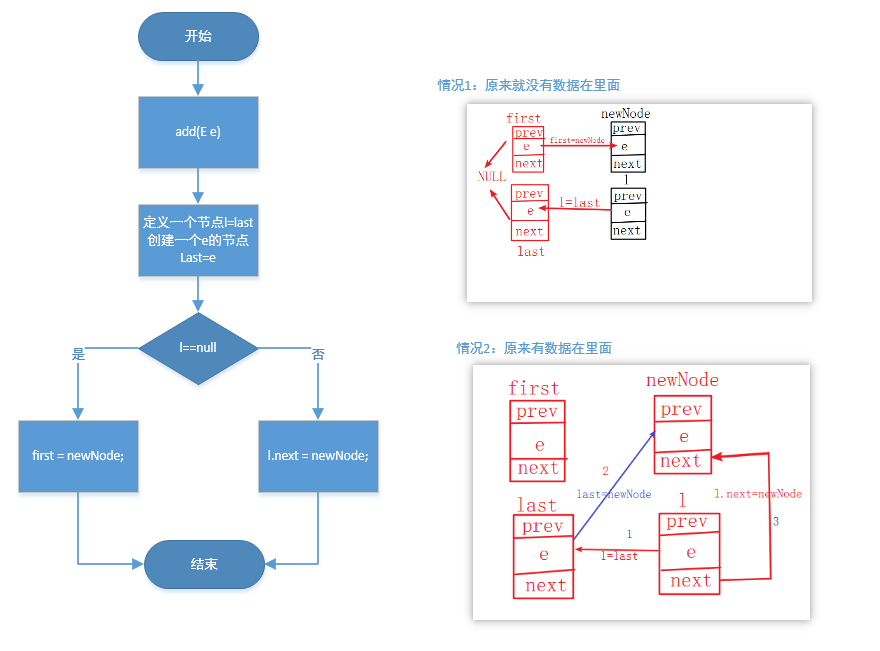
public void addFirst(E e) {//在该列表开头插入指定的元素。 linkFirst(e); } private void linkFirst(E e) {//链接e作为第一个元素。 final Node<E> f = first;//定义f比赋值first final Node<E> newNode = new Node<>(null, e, f);//创建一个节点,节点的pre为null,值为e,next为first first = newNode;//first赋值为新节点 if (f == null)//如果f==null,就是原来就没有值的情况, last = newNode;//last就为新节点 else//原来有值的情况 f.prev = newNode;原来的头节点的pre指向了新的节点 size++; modCount++; }
add(int index, E element):在此列表中指定的位置插入指定的元素。
addAll(Collection<? extends E> c):添加指定 collection 中的所有元素到此列表的结尾,顺序是指定 collection 的迭代器返回这些元素的顺序。
addAll(int index, Collection<? extends E> c):将指定 collection 中的所有元素从指定位置开始插入此列表。
2.5、移除方法
//从列表中删除指定元素的第一个出现(如果存在)。 如果此列表不包含该元素,则它将保持不变。 更正式地,删除具有最低索引的元素 public boolean remove(Object o) { if (o == null) {//如果o为null for (Node<E> x = first; x != null; x = x.next) { if (x.item == null) {//删除第一个null unlink(x);//取消链接非空节点x。 return true; } } } else { for (Node<E> x = first; x != null; x = x.next) { if (o.equals(x.item)) { unlink(x); return true; } } } return false; } E unlink(Node<E> x) {//取消链接非空节点x。 // assert x != null; final E element = x.item; final Node<E> next = x.next; final Node<E> prev = x.prev; if (prev == null) {//如果prev为null,说明是第一个节点 first = next; } else {// prev.next = next;//空掉中间的节点 x.prev = null;//原来x的prev置空 } if (next == null) {//最后一个节点, last = prev; } else {// next.prev = prev; x.next = null; } x.item = null;//置空 size--; modCount++; return element; }
2.5、查找方法
public E get(int index) {//获取index的值 checkElementIndex(index);//检查下标 return node(index).item;//获得index下的值 } Node<E> node(int index) { // assert isElementIndex(index); if (index < (size >> 1)) {//简单的使用了二分法 Node<E> x = first; for (int i = 0; i < index; i++) x = x.next; return x; } else { Node<E> x = last; for (int i = size - 1; i > index; i--) x = x.prev; return x; } }