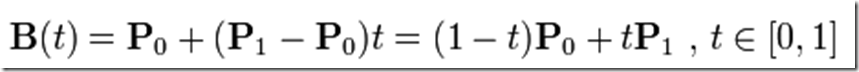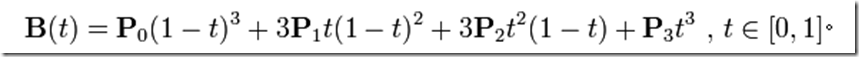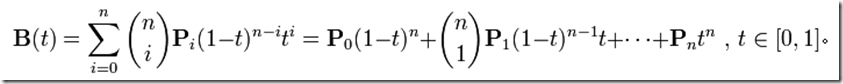CSS3中的transition和transform是制作HTML5动画一定要使用到的两个属性。
注:这篇文章不考虑兼容性,只讨论webkit核心的浏览器。所以本文的所有例子请用chrome,safari或360极速浏览器看。
transition
transition对标签的变化过程进行设置。比如我需要将这个图在2s内进行翻转180的动画,就使用到这个了
transition可以配置的属性有:
transision-property
要变化的属性,可以的参数请参考:http://www.zhangxinxu.com/css3/css3-transition-property.php
transition-duration
变化的速度,单位为s http://www.zhangxinxu.com/css3/css3-transition-duration.php
transition-timing-funtion
使用的是贝塞尔曲线的方式渐变 http://www.zhangxinxu.com/css3/css3-transition-timing-function.php
值可以是这么几个:
transition-delay
是否延迟执行变化,单位为s,默认值为0
要理解transition-timimg-funtion的几个渐变函数的意思,要知道的知识是贝塞尔曲线
贝塞尔曲线
贝塞尔曲线是计算机图形图像绘制曲线的基本工具。它的出现能使得在计算机上绘制出曲线变成可能。其中的三阶贝塞尔曲线可以通过四个点(不一定在曲线上)确定一个曲线。
贝塞尔曲线有1阶,2阶,3阶… n阶的形式
1阶的贝塞尔曲线
也称作为线性贝塞尔曲线,公式如下:
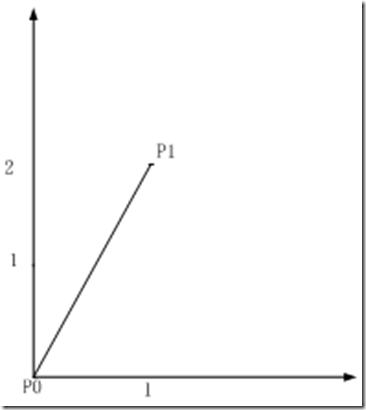
如果将1阶的贝塞尔曲线应用在坐标图上,那么这个曲线就是一条直线:
假设P0是坐标点(0,0)P1是坐标点(1, 2)。随着t从0开始不断变化成1,B(t)会得出一系列坐标点集合(这个集合当然是无限集合),将这些坐标点画成一条线,那么这条线就是一条直线
这个图画得很矬,http://zh.wikipedia.org/w/index.php?title=%E8%B2%9D%E5%A1%9E%E7%88%BE%E6%9B%B2%E7%B7%9A&variant=zh-cn 上有个动态图非常清晰
三阶的贝塞尔曲线
公式为:
这里会看到有四个系数P0,P1,P2,P3。换句话说,如果指定了这四个系数,那么我们就能得到一个贝塞尔值的集合。
这里要说一下,这四个系数可以是数值,也可以是二维坐标(比如平面坐标点),也可以是三维坐标(比如颜色RGB)。transition的timing-funtion如果作用在颜色上,这些系数就是使用三维坐标。
所以transition的timing-function这个属性的不同值就是对应了不同的P系数,其实最后呈现出来的效果就是不同的变化速度。这个页面有个例子:
http://www.funaio.com/html5/trans/transition.html
我使用ease-in和ease-out来改变图片的旋转速度,你能很明显地感觉到ease-in是在开始旋转速度慢,后来旋转速度快,ease-out则相反。
当然贝塞尔曲线是有n阶的通用形式的:
transform
transform指的是变换,一个东西的拉伸,压缩,旋转,偏移等就是使用这个属性。
transform可以设置这些函数:
rotate
将元素进行旋转,单位为deg。如rotate(45deg)
translate
将元素进行平移。这个属性是可以有两个参数的,分别表示向X轴和向Y轴进行平移的量,单位为px,第二个参数可以默认不填写
比如translate(20px,30px)
scale
将元素进行放大或缩小。记住,这里的放大和缩小不一定是维持比例的。
scale的参数有两个,分别表示向X轴和Y轴进行放大的倍数,大小在0~正无穷,第二个参数可以默认不填写,如果不填写则是默认等比放大缩小。比如scale(2)
skew
斜切变化。参数为角度deg
skew的参数有两个,分别表示X轴Y轴的斜切变化,第二个参数可以不填写,如果不填写,Y轴斜切无变化
基本的操作就是这些,这里有一篇文章有很好地例子展示:http://hi.baidu.com/rolly_zhang/item/9cc5d24b454f1f07c0161303
注:其实transform还设有一个属性matrix,这个属性是以一个含六值的(a,b,c,d,e,f)变换矩阵的形式指定一个2D变换,相当于直接应用一个[a b c d e f]变换矩阵。在下面的文章中会解释到的。
数学的角度来分析transform
w3官网上有一篇文章从数学的角度来分析transform:
http://www.w3.org/TR/SVG/coords.html
每个元素在html页面上所占有的区域称作viewport,这个区域可以建立出一个二维坐标系(Coordinate system),这个元素的所有图画上的点在二维坐标系上都有对应的x和y点
transform做的事实际上是将这个二维坐标系进行拉伸,放大,斜切变化。这个变化可以使用一个矩阵来表示:
如果原来的坐标轴表示成为1*3矩阵(这里使用1*3而不是使用1*2矩阵应该是考虑3D的变换吧,其实在介绍transform的时候,z的值一直设置为1,没有参与任何运算):
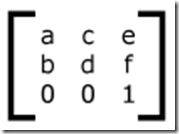
每个transform变化表示为1个3*3的矩阵(也成变化矩阵)
这里可以看到第三行为0,0,1,这就意味着这个transform不对z轴空间进行改变。因此其实上面可以填写的参数也只有6个了[a,b,c,d,e,f],看到这里就明白了transform的matrix的6个参数是什么意思
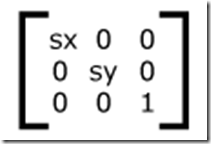
比如拉伸的变化矩阵为:
这个拉伸的变化矩阵设置了a和d,其余的设置为0
-webkit-transform:scale(2,2);
-webkit-transform:matrix(2,0,0,2,0,0);
这两个设置其实效果是一样
更多的变化矩阵请直接看w3的那篇文章
同理,如果对一个元素同时进行了拉伸和旋转效果,其实际上的效果是将拉伸的变化矩阵和旋转的变化矩阵相乘,两个3*3的矩阵相乘结果还是3*3矩阵,最后得到的矩阵才是实际的变化效果
transform-origin
下面说说transform-origin
上面说transform的变化其实是将坐标轴进行拉伸旋转等变化,那么坐标轴有一个原点,这个原点就是这个属性进行设置的了。记住,原点是永远不会变化位置的(因为它的坐标为0,0,1)。
transform-origin有两个参数,这两个参数可以是百分比,em,px等具体的值,也可以是left,center,right,top,button这样的描述性语句
就是说
-webkit-transform-origin:right top;
-webkit-transform-origin:100% 0%;
这两个其实是一样的
这里给一个例子:
其中一个图片只设置了:
.transition_function1:hover{
-webkit-transform:scale(2,2);
}
另外一个图片设置了:
.transition_function2:hover{
-webkit-transform:scale(2,2);
-webkit-transform-origin:right top;
}
点击查看效果:
http://www.funaio.com/html5/trans/transform.html
3D效果
3D效果是个很复杂的东西,以后再写一篇来专门研究吧。这里奉上几个css3 3D效果(请使用webkit浏览器):
图片翻转:
http://www.funaio.com/html5/trans/fanzhuan.html
三行翻转(有点像google图书馆):
http://www.webkit.org/blog-files/3d-transforms/poster-circle.html