Jungle Roads
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 3038 Accepted Submission(s): 2155
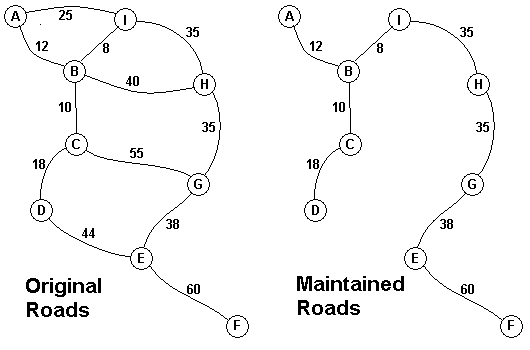
The Head Elder of the tropical island of Lagrishan has a problem. A burst of foreign aid money was spent on extra roads between villages some years ago. But the jungle overtakes roads relentlessly, so the large road network is too expensive to maintain. The Council of Elders must choose to stop maintaining some roads. The map above on the left shows all the roads in use now and the cost in aacms per month to maintain them. Of course there needs to be some way to get between all the villages on maintained roads, even if the route is not as short as before. The Chief Elder would like to tell the Council of Elders what would be the smallest amount they could spend in aacms per month to maintain roads that would connect all the villages. The villages are labeled A through I in the maps above. The map on the right shows the roads that could be maintained most cheaply, for 216 aacms per month. Your task is to write a program that will solve such problems.
The input consists of one to 100 data sets, followed by a final line containing only 0. Each data set starts with a line containing only a number n, which is the number of villages, 1 < n < 27, and the villages are labeled with the first n letters of the alphabet, capitalized. Each data set is completed with n-1 lines that start with village labels in alphabetical order. There is no line for the last village. Each line for a village starts with the village label followed by a number, k, of roads from this village to villages with labels later in the alphabet. If k is greater than 0, the line continues with data for each of the k roads. The data for each road is the village label for the other end of the road followed by the monthly maintenance cost in aacms for the road. Maintenance costs will be positive integers less than 100. All data fields in the row are separated by single blanks. The road network will always allow travel between all the villages. The network will never have more than 75 roads. No village will have more than 15 roads going to other villages (before or after in the alphabet). In the sample input below, the first data set goes with the map above.
The output is one integer per line for each data set: the minimum cost in aacms per month to maintain a road system that connect all the villages. Caution: A brute force solution that examines every possible set of roads will not finish within the one minute time limit.
#include<stdio.h> #include<string.h> #define MAXN 1000; #define NUM 30 int Graph[30][30]; int Traverse(int n) { int i, j; for(i=0; i<n; ++i) { for(j=0; j<n; ++j) printf("%3d ", Graph[i][j]); printf("\n"); } } int Prim(int n) { int i, j, k, t, flag[30], closedge[30], ans = 0; for(i=1; i<n; ++i) { closedge[i] = Graph[0][i]; flag[i] = 0; } flag[0] = 1; for(i=1; i<n; ++i) { k = 1, t = MAXN; for(j=1; j<n; ++j) if(!flag[j] && closedge[j] < t) k = j, t = closedge[j]; ans += t; flag[k] = 1; for(j=0; j<n; ++j) if(!flag[j] && Graph[k][j] < closedge[j]) closedge[j] = Graph[k][j]; } return ans; } int main() { int i, j, len, flag, ti, tj, n, w, m; char alpha; while(scanf("%d", &n) == 1 && n) { getchar(); for(i=0; i<n; ++i) for(j=0; j<n; ++j) Graph[i][j] = MAXN; for(i=1; i<n; ++i) { scanf("%c %d", &alpha, &m); ti = alpha-65; for(j=0; j<m; ++j) { scanf(" %c %d", &alpha, &w); tj = alpha - 65; Graph[ti][tj] = Graph[tj][ti] = w; } getchar(); } // Traverse(n); printf("%d\n", Prim(n)); } return 0; }
解题报告:
第一次写最小生成树(MST),觉得有必要写写思路,加深印象,尽管看起来像模板
首先设连通网为N = (V, {E}), 用邻接表建立图结构时,需将无邻接两节点之间边的权值用最大值MAXN表示。
初始化需将始点V。放入最小生成树的圈内用(U表示),标记在U中用数组 flag[ i ] = 1表示,否则为0(0<=i<=n),开一个数 组closedge[ i ] (0<=i<=n),开始时存储的是始点V。相关联边的权值,i为各自相关联边的邻接点。
for(first)循环: from 1 to (n-1) 确保最后所有的节点都放入到U中形成最小生成树
for(second)循环: 找到圈外一节点与U中节点(根据下面的for循环,可以保证一直都存在这个条件)权值达到最小,通过 t变量的不断减小来实现此功能
因为for(second)循环 和 for(first)循环从节点数的角度来看是同步,所以for(second) 中肯定会找到一个符合条件的k, 此时通过赋值flag[k]为1加入U中
其他需要的操作以实现题目的要求
for(second)循环:可以这样说,k节点的加入,对于U这个家庭来说,“带来了希望和新鲜的血液”,k与外面的节点可能更 亲切(与外面节点之间的权值更小),通过此for循环,找出更小的路径——只能在k身上发生,否则没有改变
end(first for)
其中起重要作用的是flag[]——标记数组,它会让你放心的将U中的节点的其他信息避而不谈。
