【数据结构】：算法（一）

算法基础

1、什么是算法？

算法（Algorithm）：一个计算过程，解决问题的方法

2、复习：递归

递归的两个特点：

• 调用自身
• 结束条件

两个重要递归函数的对比：

# 由大到小
def func3(x):
    if x > 0 :
        print(x)
        func3(x-1)

# func3(5)
# 5 4 3 2 1

# 由小到大
def func4(x):
    if x > 0 :
        func4(x-1)
        print(x)

func4(5)
# 1 2 3 4 5

　　

3、时间复杂度

时间复杂度：用来评估算法运行效率的一个东西：

print('Hello World')            # 0(1)

for i in range(n):                  # O(n)
    print('Hello World')

for i in range(n):                   # O(n^2)
    for j in range(n):
        print('Hello World')

for i in range(n):                   # O(n^3)
    for j in range(n):
        for k in range(n):
            print('Hello World')

第一个打印了一次时间复杂度为O(1)；第二个打印了n次，所以时间复杂度为O(n);第三四个依次为n²和n的3次方

那么看看下面代码中的时间复杂度为多少?

# 非O(3) 而是O(1)
print('Hello World')
print('Hello Python')
print('Hello Algorithm')

# 非O(n²+n) 而是O(n²)
for i in range(n):
    print('Hello World')
        for j in range(n):
            print('Hello World')

# 非O(1/2n²) 而是O(n2)
for i in range(n):
    for j in range(i): 
        print('Hello World')

再看看下面代码：　

# 时间复杂度 O(log2n) 或 O(logn)
while n > 1:
    print(n)
    n = n // 2

# n=64输出：
# 64
# 32
# 16
# 8
# 4
# 2

小结：

时间复杂度是用来估计算法运行时间的一个式子（单位）。

一般来说，时间复杂度低的算法比复杂度低的算法快。

常见的时间复杂度（按用时排序）

• O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n2logn)<O(n3)

不常见的时间复杂度（看看就好）

• O(n!) O(2n) O(nn) …

如何一眼判断时间复杂度？

• 循环减半的过程O(logn)
• 几次循环就是n的几次方的复杂度

4、空间复杂度

空间复杂度：用来评估算法内存占用大小的一个式子

列表查找

列表查找：从列表中查找指定元素

• 输入：列表、待查找元素
• 输出：元素下标或未查找到元素

1、顺序查找

从列表第一个元素开始，顺序进行搜索，直到找到为止

def linear_search(data_set, value):  
    for i in data_set:       
        if data_set[i] == value:    
            return i  
    return

时间复杂度为O(n)

2、二分查找

从有序列表的候选区data[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半

# 正宗的二分查找
data = [i for i in range(9000000)]
import time
def cal_time(func):
    def inner(*args,**kwargs):
        t1 = time.time()
        re =  func(*args,**kwargs)
        t2 = time.time()
        print('Time cost:',func.__name__,t2-t1)
        return re
    return inner

@cal_time
def bin_search(data_set,val):
    low = 0
    high = len(data_set) - 1
    while low <= high:
        mid = (low + high)//2
        if data_set[mid] == val:
            return mid
        elif data_set[mid] < val:
            low = mid +1
        else:
            high = mid -1

bin_search(data, 999)
# Time cost: bin_search 0.0005002021789550781

时间复杂度为O(logn),运行后会发现执行的很快，下面对比下之前Alex讲过的二分查找

# Alex的low版本
data = [i for i in range(9000000)]
import time
def cal_time(func):
    def inner(*args,**kwargs):
        t1 = time.time()
        re =  func(*args,**kwargs)
        t2 = time.time()
        print('Time cost:',func.__name__,t2-t1)
        return re
    return inner

def _binary_search(dataset, find_num):
    if len(dataset) > 1:
        mid = int(len(dataset) / 2)
        if dataset[mid] == find_num:  # find it
            print("找到数字", dataset[mid])
        elif dataset[mid] > find_num:  # 找的数在mid左面
            return _binary_search(dataset[0:mid], find_num)
        else:  # 找的数在mid右面
            return _binary_search(dataset[mid + 1:], find_num)

@cal_time
def binary_search(dataset, find_num):
    _binary_search(dataset, find_num)

binary_search(data, 999)
# Time cost: binary_search 0.4435563087463379

3、练习　　

现有一个学员信息列表（按id增序排列），格式为：

[
{id:1001, name:"张三", age:20},
{id:1002, name:"李四", age:25},
{id:1004, name:"王五", age:23},
{id:1007, name:"赵六", age:33}
]

修改二分查找代码，输入学生id，输出该学生在列表中的下标，并输出完整学生信息

import random
import time

# 生成随机列表
def  random_list(n):
    result = []
    ids = list(range(1001,1001+n))
    n1 = ['赵','王','孙','李']
    n2 = ['国','爱','清','菲','']
    n3 = ['甄','轩','雨','军']
    for i in range(n):
        age = random.randint(18,60)
        id = ids[i]
        name = random.choice(n1)+random.choice(n2)+random.choice(n3)
        dic = {'id':id,'name':name,'age':age}
        result.append(dic)
    return result

# 二分查找
def cal_time(func):
    def inner(*args,**kwargs):
        t1 = time.time()
        re =  func(*args,**kwargs)
        t2 = time.time()
        print('Time cost:',func.__name__,t2-t1)
        return re
    return inner

@cal_time
def bin_search(data_set,val):
    low = 0
    high = len(data_set) - 1
    while low <= high:
        mid = (low + high)//2
        if data_set[mid]['id'] == val:
            return mid
        elif data_set[mid]['id'] < val:
            low = mid +1
        else:
            high = mid -1


student_list = random_list(100000)
bin_search(student_list, 999)
# Time cost: bin_search 0.0004999637603759766

列表排序（lowB三人组）

概述

列表排序：

将无序列表变为有序列表

应用场景：

• 各种榜单
• 各种表格
• 给二分排序用
• 给其他算法用

排序low B三人组：
冒泡排序
选择排序
插入排序
快速排序
排序NB二人组：
堆排序
归并排序
没什么人用的排序：
基数排序
希尔排序
桶排序

1、冒泡排序（low）

排序思路：首先，列表每两个相邻的数，如果前边的比后边的大，那么交换这两个数，每次循环都会选中一个最大的数，然后依次把列表排序；

import random
import time

def call_time(func):
    def inner(*args,**kwargs):
        t1 = time.time()
        re = func(*args,**kwargs)
        t2 = time.time()
        print('Time cost:',func.__name__,t2-t1)
        return re
    return inner

@call_time
def bubble_sort(data):
    for i in range(len(data)-1):
        for j in range(len(data)-i-1):
            if data[j] > data[j+1]:
                data[j],data[j+1] = data[j+1],data[j]
    return data
data = list(range(10000))
random.shuffle(data)

bubble_sort(data)
# Time cost: bubble_sort 17.608235836029053

时间复杂度：O(n²)

优化：

@call_time
def bubble_sort_1(data):
    for i in range(len(data)-1):
        exchange = False                # 没有交换 表示前边都已经排好了 执行退出
        for j in range(len(data)-i-1):
            if data[j] > data[j+1]:
                data[j],data[j+1] = data[j+1],data[j]
                exchange = True
        if not exchange:
            break
    return data

　　

2、选择排序（low）

排序思路：一趟遍历记录最小的数，放到第一个位置； 再一趟遍历记录剩余列表中最小的数，继续放置；或遍历最大的放到最后

import random
import time

def call_time(func):
    def inner(*args,**kwargs):
        t1 = time.time()
        re = func(*args,**kwargs)
        t2 = time.time()
        print('Time cost:',func.__name__,t2-t1)
        return re
    return inner

@call_time
def select_sort(li):
    for i in range(len(li)-1):
        max_loc = 0
        for j in range(len(li)-i-1):
            if li[max_loc] < li[j]:
                max_loc = j
        li[len(li)-i-1],li[max_loc] = li[max_loc],li[len(li)-i-1]


data = list(range(10000))
random.shuffle(data)

select_sort(data)
# Time cost: select_sort 10.837876319885254

时间复杂度：O(n²)　　

def select_sort(li):
    for i in range(len(li)-1):
        min_loc = i
        for j in range(i+1,len(li)):
            if li[j] < li[min_loc]:
                min_loc = j
        li[i],li[min_loc] = li[min_loc],li[i]

3、插入排序（low）

插入思路：列表被分为有序区和无序区两个部分。最初有序区只有一个元素。 每次从无序区选择一个元素，插入到有序区的位置，直到无序区变空

import random
import time

def call_time(func):
    def inner(*args,**kwargs):
        t1 = time.time()
        re = func(*args,**kwargs)
        t2 = time.time()
        print('Time cost:',func.__name__,t2-t1)
        return re
    return inner

@call_time
def insert_sort(li):
    for i in range(1,len(li)):
        for k in range(i-1,-1,-1):
            if li[i] < li[k]:
                li[i],li[k] = li[k],li[i]
                i = k
            else:
                break

data = list(range(10000))
random.shuffle(data)

insert_sort(data)
# Time cost: insert_sort 9.358688592910767

时间复杂度：O(n²)　　

def insert_sort(li):
    for i in range(1,len(li)):
        tmp = li[i]
        j = i -1 
        while j >=0 and li[j] > tmp:
            li[j+1] = li[j]
            j = j -1
        li[j+1] = tmp

快速排序

快速排序：快

• 好写的排序算法里最快的
• 快的排序算法里最好写的

快排思路：

• 取一个元素p（第一个元素），使元素p归位；
• 列表被p分成两部分，左边都比p小，右边都比p大；
• 递归完成排序。

示图：

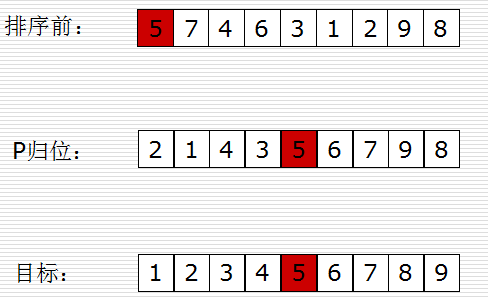
记住要领：

• 右手左手一个慢动作！右手左手慢动作重播

代码：

import random
import time

def call_time(func):
    def inner(*args,**kwargs):
        t1 = time.time()
        re = func(*args,**kwargs)
        t2 = time.time()
        print('Time cost:',func.__name__,t2-t1)
        return re
    return inner

def quick_sort_x(data,left,right):
    if left < right:
        mid = partition(data,left,right)
        quick_sort_x(data,left,mid-1)
        quick_sort_x(data,mid+1,right)

def partition(data,left,right):
    tmp = data[left]
    while left < right:
        while left < right and data[right] >= tmp:
            right -=1
        data[left] = data[right]
        while left < right and data[left] <= tmp:
            left +=1
        data[right] = data[left]
    data[left] = tmp
    return left

@call_time
def quick_sort(data):
    quick_sort_x(data, 0, len(data)-1)


data = list(range(10000))
random.shuffle(data)

quick_sort(data)
#Time cost: quick_sort 0.05100655555725098

时间复杂度：O(nlogn)