方向余弦阵，欧拉角，四元数

1，方向余弦阵

坐标变换矩阵的每一个元素都是i系某个坐标系与b系坐标系的夹角的余弦。这个转换方法也同样适用于二维坐标转换。只不过二维坐标转换不仅需要考虑旋转，同时也需要考虑坐标的平移变换。

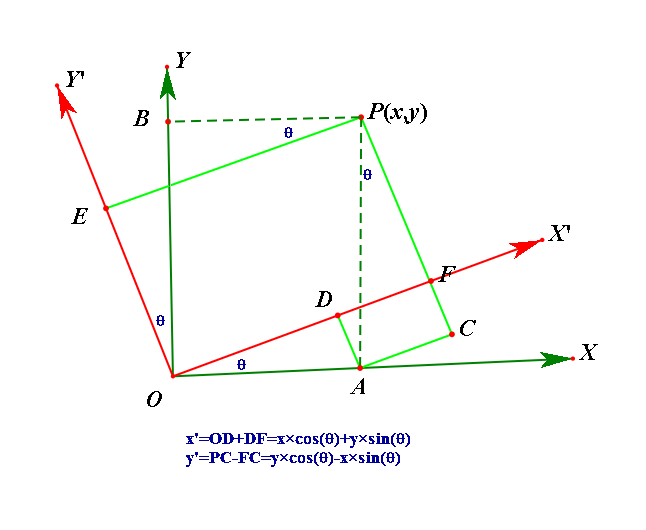
如上图所示，表示只进行旋转的时候二维坐标转换公式。此时旋转矩阵表示为P=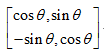

2，欧拉角

 经典的欧拉角有多种定义，下面只介绍内旋方式的定义。

 

所以，欧拉角只是绕着两个本机坐标轴在旋转，第三个坐标轴就没有用到。

之后提出 Tait-Bryan 角

经常说的yaw，pitch，roll就是用Tait-Bryan角实现的。并且yaw指的是绕z轴旋转的角度值，pitch指的是绕y轴旋转的角度值，roll指的是绕x轴旋转的角度值。

通常yaw角也用ψ表示，pitch角也用θ表示，roll角也用φ表示。并且yaw和roll的范围是[-∏,∏],pitch的范围是[-Π/2,Π/2].

不同的旋转组合虽然可以得到相同的坐标转换结果，但是得到的roll，pitch，yaw是不同的。

按照x，y，z顺序旋转得到由roll，pitch，yaw表示的方向余弦如下

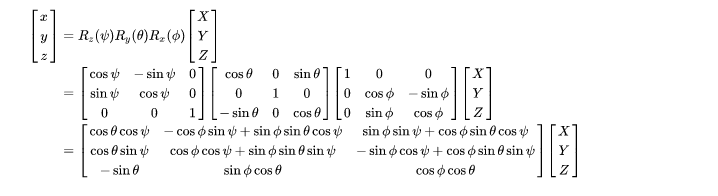
由方向余弦得到roll pitch yaw的表达式如下

roll(φ)=atan2(R(3,2),R(3,3));

pitch(θ)=-asin(R(3,1));

yaw(ψ)=atan2(R(2,1),R(1,1));

3,四元数

四元数的理解可以参考http://www.qiujiawei.com/understanding-quaternions/（理解四元数，比较通俗的解释了四元数）

推导请查看秦永元版惯性导航中相关章节。

四元数的几何意义：实部表示旋转角度的1/2的余弦值。虚部表示旋转轴与旋转角度的1/2的正弦值的乘积。

四元数得到方向余弦矩阵的表达式

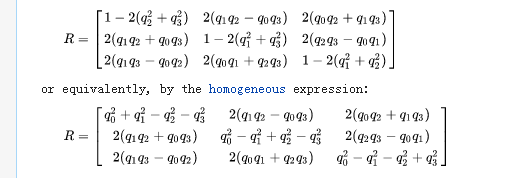
上式和下式是相同的，因为四元数的平方和等于1。

由方向余弦阵到四元数的转换可以参考以下matlab程序

function q=dcm2q(R)

T = 1 + R(1,1) + R(2,2) + R(3,3);

if T > 10^-8
    
    S = 0.5 / sqrt(T);
    qw = 0.25 / S;
    qx = ( R(3,2) - R(2,3) ) * S;
    qy = ( R(1,3) - R(3,1) ) * S;
    qz = ( R(2,1) - R(1,2) ) * S;

else
    
    if (R(1,1) > R(2,2)) && (R(1,1) > R(3,3))
        
        S = sqrt( 1 + R(1,1) - R(2,2) - R(3,3)) * 2; % S=4*qx
        qw = (R(3,2) - R(2,3)) / S;
        qx = 0.25 * S;
        qy = (R(1,2) + R(2,1)) / S;
        qz = (R(1,3) + R(3,1)) / S;
        
    elseif (R(2,2) > R(3,3))
        
        S = sqrt( 1 + R(2,2) - R(1,1) - R(3,3) ) * 2; %S=4*qy
        qw = (R(1,3) - R(3,1)) / S;
        qx = (R(1,2) + R(2,1)) / S;
        qy = 0.25 * S;
        qz = (R(2,3) + R(3,2)) / S;

    else
        
        S = sqrt( 1 + R(3,3) - R(1,1) - R(2,2) ) * 2; % S=4*qz
        qw = (R(2,1) - R(1,2)) / S;
        qx = (R(1,3) + R(3,1)) / S;
        qy = (R(2,3) + R(3,2)) / S;
        qz = 0.25 * S;

    end

end
q = [qx qy qz qw]';
end

4，方向余弦阵的微分

5，四元数微分

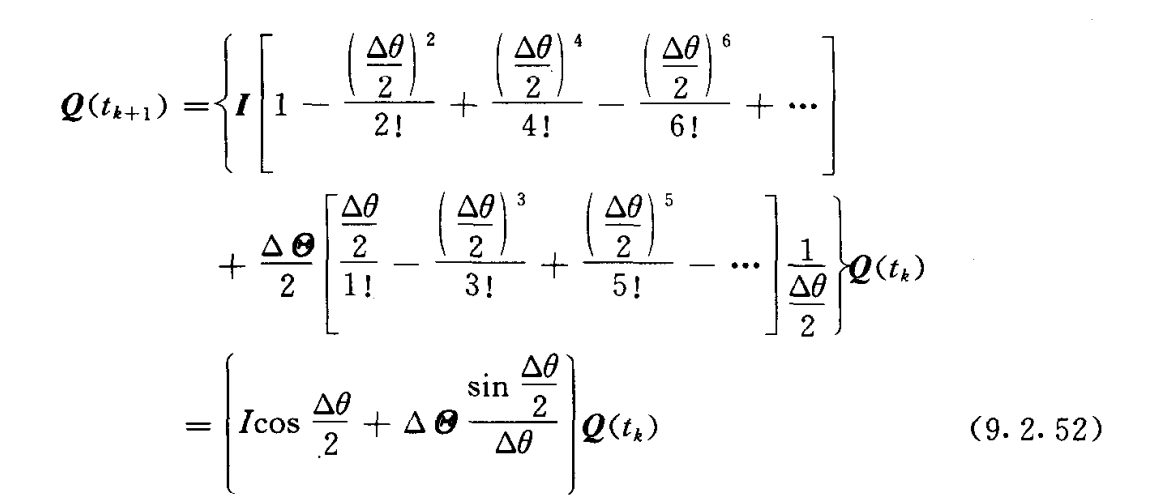
详细的推导参看秦永元版惯性导航