什么是贪心算法
贪心算法(英语:greedy algorithm),又称贪婪算法,是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法。
——维基百科
贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择,不能回退。动态规划则会保存以前的运算结果,并根据以前的结果对当前进行选择,有回退功能。
实际上,贪心算法适用的场景比较有限。这种算法思想更多的是指导设计基础算法。比如最 小生成树算法、单源最短路径算法,这些算法都用到了贪心算法。
贪心算法解决问题的步骤
第一步,当我们看到这类问题的时候,首先要联想到贪心算法:针对一组数据,我们定义了限制值和期望值,希望从中选出几个数据,在满足限制值的情况下,期望值最大。
第二步,我们尝试看下这个问题是否可以用贪心算法解决:每次选择当前情况下,在对限制 值同等贡献量的情况下,对期望值贡献最大的数据。
第三步,我们举几个例子看下贪心算法产生的结果是否是最优的。
贪心算法实战
1.分糖果
问题:我们有m个糖果和n个孩子。我们现在要把糖果分给这些孩子吃,但是糖果少,孩子多 (m < n),所以糖果只能分配给一部分孩子。
抽象:从n个孩子中,抽取一部分孩子分配糖果,让满足的孩子的个数 (期望值)是最大的。这个问题的限制值就是糖果个数m。
解题思路:从需求小的孩子开始分配糖果。
2.钱币找零
问题:假设我们有1元、2元、5元、10元、20元、50元、 100元这些面额的纸币,它们的张数分别是c1、c2、c5、c10、c20、c50、c100。我们现在 要用这些钱来支付K元,最少要用多少张纸币呢?
解题思路:是先用面值最大的来支付,如果不够,就继续用更小一点面值的,以此 类推,最后剩下的用1元来补齐
3.区间覆盖
问题:假设我们有n个区间,区间的起始端点和结束端点分别是[l1, r1],[l2, r2],[l3, r3],……,[ln, rn]。我们从这n个区间中选出一部分区间,这部分区间满足两两不相交(端点相交的情况不算 相交),最多能选出多少个区间呢?
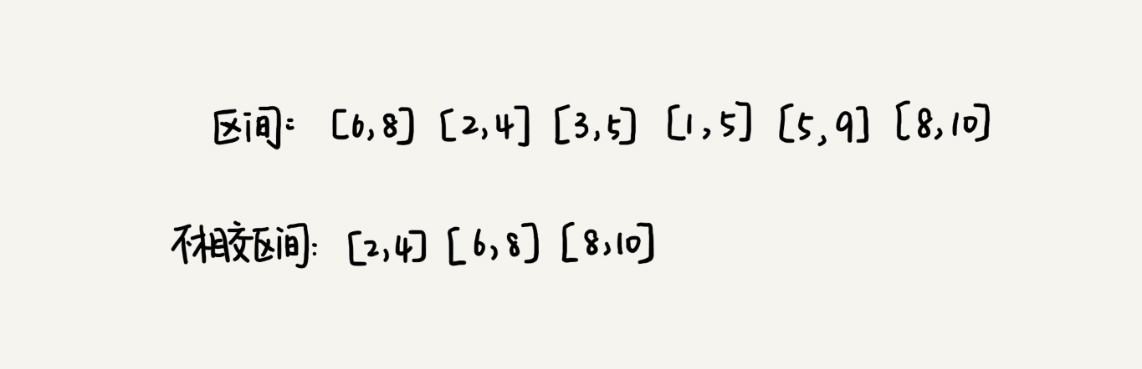
解题思路:
我们假设这n个区间中最左端点是lmin,最右端点是rmax。这 个问题就相当于,我们选择几个不相交的区间,从左到右将[lmin, rmax]覆盖上。我们按照起 始端点从小到大的顺序对这n个区间排序。
我们每次选择的时候,左端点跟前面的已经覆盖的区间不重合的,右端点又尽量小的,这样 可以让剩下的未覆盖区间尽可能的大,就可以放置更多的区间。