概念
树:是一种数据结构,像一颗倒挂的树。树的每个元素叫作“节点”;用来连续相邻节点之间的关系,叫作“父子关系”。
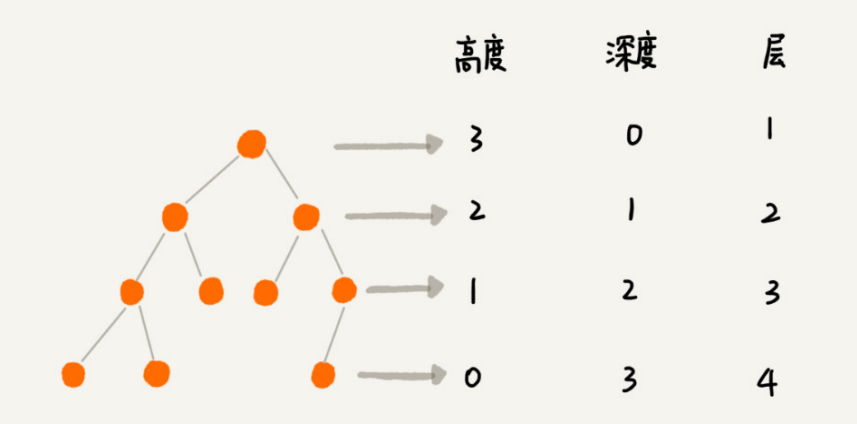
关于高度(Height)、深度(Depth)、层(Level)
- 节点的高度=节点到叶子节点的最长路径(边数)。
- 节点的深度=根节点到这个节点所经历的边的个数。
- 节点的层数=节点的深度+1。
- 树的高度=根节点的高度。
关于二叉种种类:
- 二叉树:每个节点最多有两个子节点的树。
- 满二叉树:除叶子节点外,每个节点都有左右的子节点的树。
- 完全二叉树:叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大。
如何存储
要存储一棵二叉树,有两种方法,一种是基于指针的链式存储,一种是基于数组的顺序存储。
链式存储法
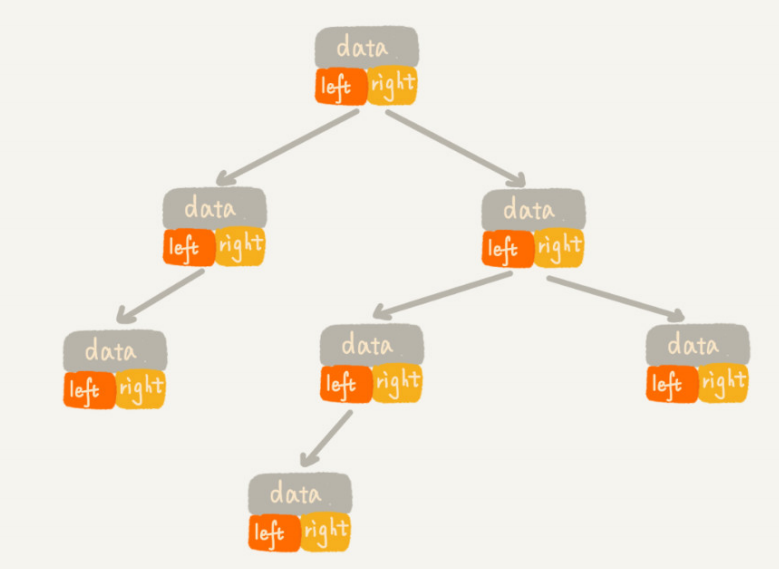
顺序存储法
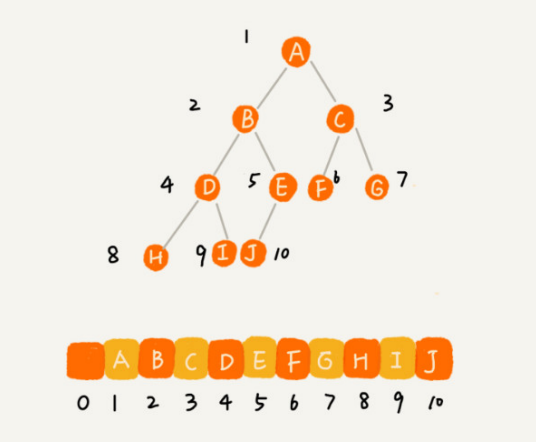
存储方式:如果节点X存储在数组中下标为i的位置,
- 下标为2 * i的位置存储的是左子节点;
- 下标为2 * i + 1的位置存储的是右子节点;
- 下标为i / 2的位置存储的是父节点;
注:如果存储的不是完全二叉树,会浪费比较多的空间,二叉树越稀疏,浪费的空间越多。
二叉树的遍历
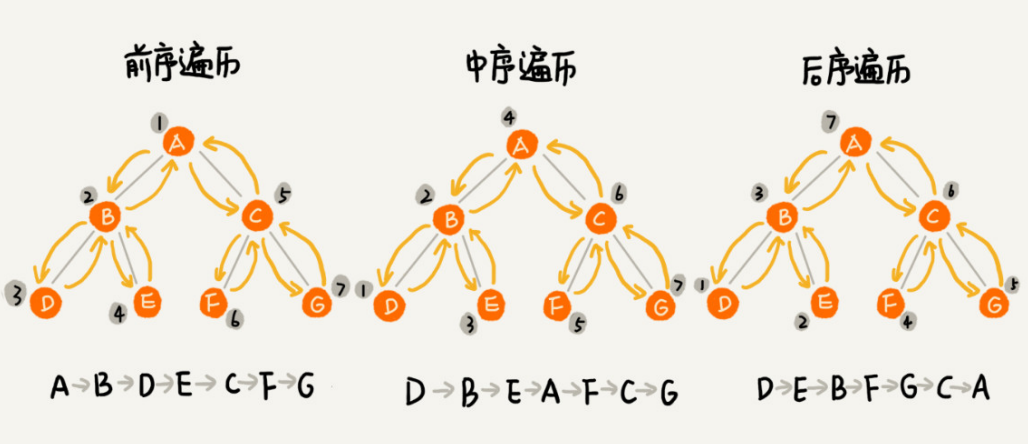
经典的方法有三种,前序遍历、中序遍历和后序遍历。
- 前序遍历:对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
- 中序遍历:对于树中的任意节点来说,先打印它的左子树,然后打印它本身,最后打印它的右子树。
- 后序遍历:对于树中的任意节点来说,先打印它的左子树,然后打印它的右子树,最后打印这个节点本身。
实现代码:
void preOrder(Node* root) {
if (root == null) return;
print root // 此处为伪代码,表示打印root节点
preOrder(root->left);
preOrder(root->right);
}
void inOrder(Node* root) {
if (root == null) return;
inOrder(root->left);
print root // 此处为伪代码,表示打印root节点
inOrder(root->right);
}
void postOrder(Node* root) {
if (root == null) return;
postOrder(root->left);
postOrder(root->right);
print root // 此处为伪代码,表示打印root节点
}
时间复杂度:O(n)。前、中、后序遍历对每个节点最多访问两次。
课后思考
1.给定一组数据,比如1,3,5,6,9,10。你来算算,可以构建出多少种不同的二叉树?
有两个因素:
- n个数构成的二叉树有a种
- n个数的组合有b种。
结果等于a * b。即卡塔兰数。https://en.wikipedia.org/wiki/Catalan_number
2.我们讲了三种二叉树的遍历方式,前、中、后序。实际上,还有另外一种遍历方式,也就是按层遍历,你知道如何实现吗?
利用队列的特性,步骤如下:
- 当前节点(第一个元素是根节点)入队(当前层数为1),然后指针指向当前节点。
- 把当前节点的子节点入队,并记录当前层数(当前节点层数+1)。
- 循环1-2步,直到指针指向队尾。
- 此时队列是按层序遍历的链式队列。
- 遍历队列输出即可。
代码实现:
/**
* Definition for a binary tree node.
* public class TreeNode {
* public int val;
* public TreeNode left;
* public TreeNode right;
* public TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public IList<int> LevelOrder(TreeNode root)
{
if (root == null) return new List<IList<int>>();
TreeLinkedList head = new TreeLinkedList(null, -1);
head.next = new TreeLinkedList(root, 1);
TreeLinkedList curr = head.next;
TreeLinkedList tail = head.next;
while (curr != null)
{
if (curr.node.left != null)
{
tail.next = new TreeLinkedList(curr.node.left, curr.level + 1);
tail = tail.next;
}
if (curr.node.right != null)
{
tail.next = new TreeLinkedList(curr.node.right, curr.level + 1);
tail = tail.next;
}
curr = curr.next;
}
IList<int> result = new List<int>();
curr = head.next;
while (curr != null)
{
result .Add(curr.node.val);
curr = curr.next;
}
return result;
}
public class TreeLinkedList
{
public TreeNode node;
public int level;
public TreeLinkedList next;
public TreeLinkedList(TreeNode node, int level)
{
this.node = node;
this.level = level;
}
}
}