第350题:
给定两个数组,编写一个函数来计算它们的交集。来源:力扣(LeetCode)
示例 1:
输入: nums1 = [1,2,2,1], nums2 = [2,2]
输出: [2,2]
示例 2:
输入: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出: [4,9]
说明:输出结果中每个元素出现的次数,应与元素在两个数组中出现的次数一致。我们可以不考虑输出结果的顺序。
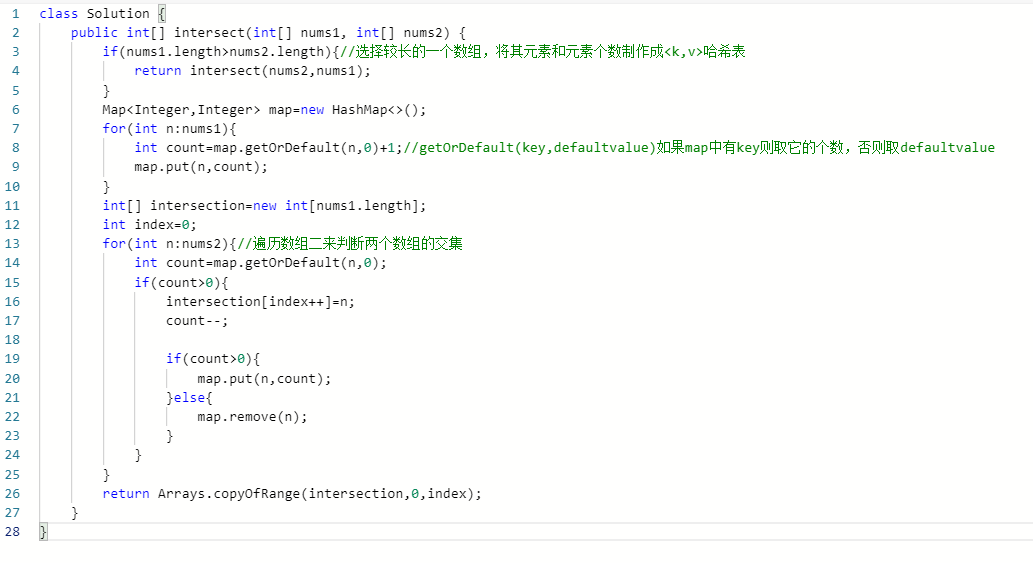
1、求两个数组的交集,就是判断数组内有多少个相同的元素,
直接用哈希表将长的数组内的元素和此元素个数作为key和valueput进hashmap中;
然后遍历数组二,当里面出现一个hashmap里面有的元素,就将hashmap中这个key对应的value-1;
所以不管有没有重复的相同元素,也可以取出来,用数组接收;
最终返回所需结果。
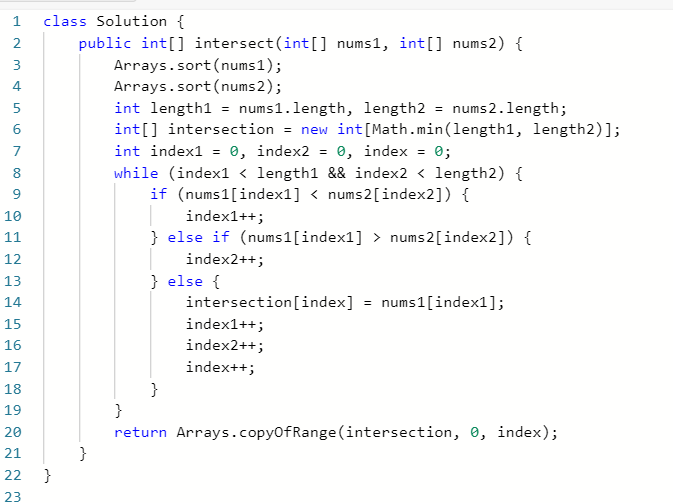
2、也可以先将两个数组排好序,然后用两个指针分别遍历两个数组,就可以得出两个数组的交集了。
第29题:
给定两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。
返回被除数 dividend 除以除数 divisor 得到的商。
整数除法的结果应当截去(truncate)其小数部分,例如:truncate(8.345) = 8 以及 truncate(-2.7335) = -2来源:力扣(LeetCode)
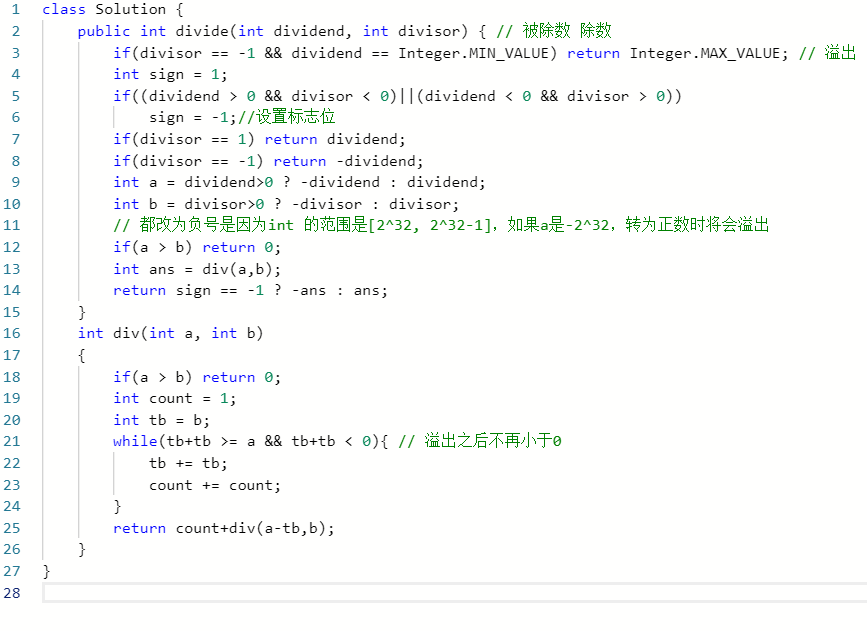
1、求被除数除以除数的商,不能使用乘法除法和mod运算符;
其实就是运算被除数里面包含了count个除数,可以用单纯的一个一个减来得出结果,但是好像时间超出限制;
对于结果的正负,可以设置一个标志位来直接判断;
由于数值的范围为int类型,所以可以将被除数和除数都转换为负数(因为有标志位,所以不妨碍结果);
对于被除数和除数,可以使用被除数减去2^n个除数来计算count个数,可降低运行时间;
先求出被除数可蕴含除数的最大个数,按照二次幂个数相加;
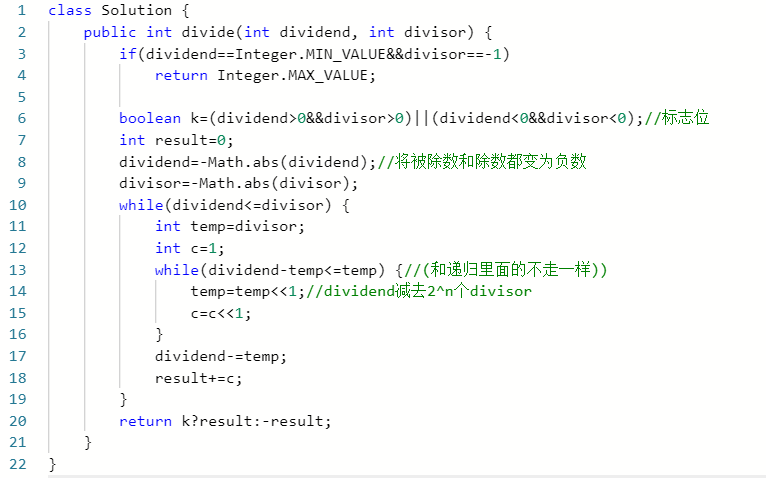
例如被除数时11除数是3时,3<11,所以count肯定可以=1,所以将3翻倍,count也翻倍,得到6,6也<11,所以count肯定也可以等于2;
当此时再次翻倍时,除数变为了12,但是12>11,所以除数和count不能再增加了,所以被除数=11-6=5;
这时候就可以将5作为被除数来和除数3再次计算余下的count个数,求处累加到上面的count,得出最终结果;
最后以标志位来判断count的正负。
第35题:
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。(来自LeetCode)
1、直接遍历数组,将插入位置找到。
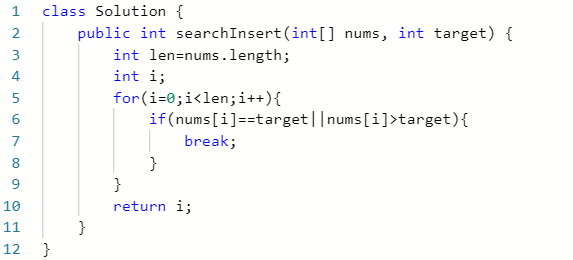
2、利用二分查找寻找插入位置。
