说是第二天,但我昨天太懒没写,今天一起补上吧。
PART ONE : DP复习一

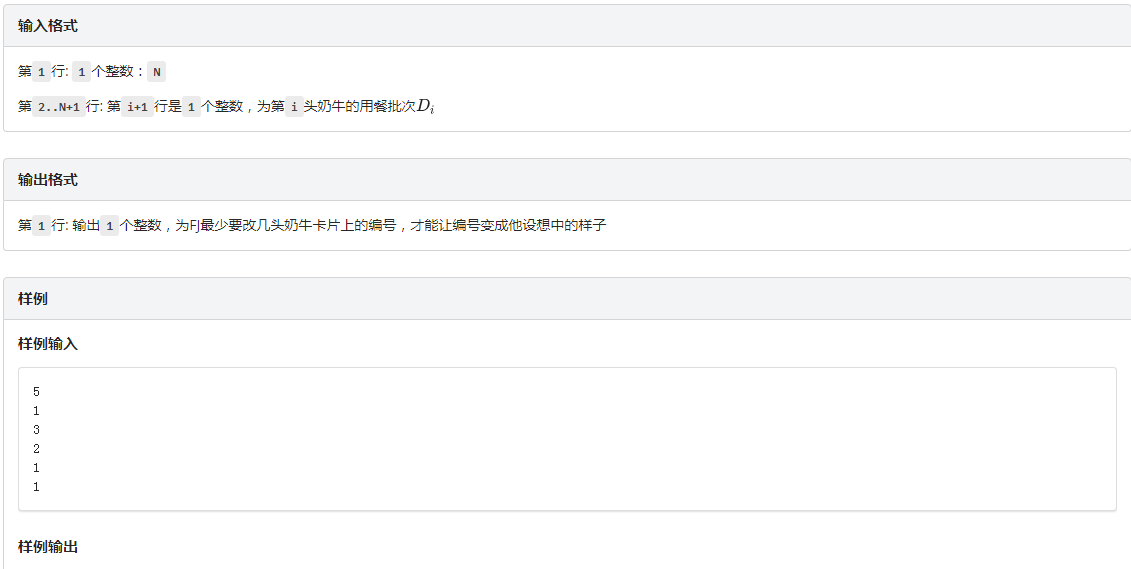

分析:其实这道题本身并不难,就是正反跑一遍最大上升子序列,求一个和总长度最小的差值就行了,但是这道题有一组神奇的数据导致n^3的方法过不去,我正好又不会写二分,于是......
于是我想趁机说一下二分的有关事项,代码在下面,但是对于可以二分的题我们可以尝试使用lower_bound和upper_bound,我暂时只会用单调上升的,下降的它会返回一些奇奇怪怪的数,他们的功能是这样的,如果我们查找的数在序列中没有,那么他们两个的作用都是返回最后一个小于所查数的位置(注意是位置,在最后要减去数组位置,从1开始的数组要减a+1),如果所查数存在,lower_bound作用不变,upper_bound变为返回位置最大的所查数的位置,比较麻烦,所以以后能手写二分还是手写吧.......
代码:

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 const int N=1e6+10; 5 using namespace std; 6 int erfen(int *a,int r,int x){ 7 int l=1,mid; 8 while(l<=r){ 9 mid=(l+r)>>1; 10 if(a[mid]<=x) l=mid+1; 11 else r=mid-1; 12 } 13 return l; 14 } 15 int a[N],b[N],c[N],sum,ans1,ans2; 16 int main(){ 17 //freopen("a.in","r",stdin); 18 int n; 19 scanf("%d",&n); 20 for(int i=1;i<=n;++i){ 21 scanf("%d",&a[i]); 22 b[n-i+1]=a[i]; 23 } 24 c[1]=a[1];sum=1; 25 for(int i=2;i<=n;++i){ 26 if(a[i]>=c[sum]) c[++sum]=a[i]; 27 else if(a[i]<c[sum]){ 28 int t=erfen(c,sum,a[i]); 29 c[t]=a[i]; 30 } 31 } 32 ans1=n-sum; 33 memset(c,0,sizeof(c));sum=1;c[1]=b[1]; 34 for(int i=2;i<=n;++i){ 35 //for(int j=1;j<=sum;++j) printf("%d ",c[j]); puts(""); 36 if(b[i]>=c[sum]) c[++sum]=b[i]; 37 else if(b[i]<c[sum]){ 38 int t=erfen(c,sum,b[i]); 39 c[t]=b[i]; 40 } 41 } 42 ans2=n-sum; 43 printf("%d ",min(ans1,ans2)); 44 return 0; 45 }

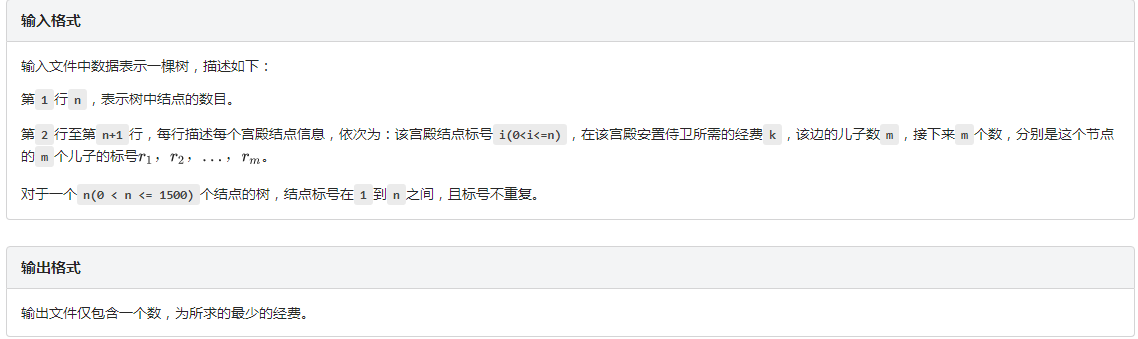

分析:long long age,某姚姓教练曾讲过这道题,但既然我把它放在了这里,显然我又错了啊,我又被老姚抓住我上课没认真听讲了.
这次练习中有几道树形DP的题,但是这道比较不同,想我自己写出的没有上司的舞会和三色二叉树,都是父节点通过子节点转移,而这道题还需要考虑父亲节点的情况,一个父亲节点如果自己不设防,父亲的父亲不设防,那么它至少一个儿子要设防,我们可以对每个儿子的设防花费和不设防花费的差取最小,如果此差值大于零,那么就表示没有一个儿子愿意设防来看护它们的老父亲,我们把上面的差值再加回去,就可以强迫一个最优的儿子尽孝,之后的转移就好说了,如果一个节点自己设防,儿子三种情况都要比较,如果不设防或自己不设防父亲设防,排除子节点的父亲设防情况即可.
代码:

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 const int N=1e4; 5 int dp[N][5],val[N]; 6 struct Node{ 7 int next,to; 8 }edge[N]; 9 int Head[N],tot; 10 int n; 11 void Add(int x,int y){ 12 edge[++tot].to=y; 13 edge[tot].next=Head[x]; 14 Head[x]=tot; 15 } 16 void dfs(int x){ 17 dp[x][0]=val[x]; 18 int cha=0x3f3f3f3f; 19 for(int i=Head[x];i;i=edge[i].next){ 20 int v=edge[i].to; 21 dfs(v); 22 dp[x][0]+=min(dp[v][0],min(dp[v][1],dp[v][2])); 23 dp[x][1]+=min(dp[v][0],dp[v][2]); 24 dp[x][2]+=min(dp[v][0],dp[v][2]); 25 cha=min(cha,dp[v][0]-dp[v][2]); 26 } 27 if(cha>0) dp[x][2]+=cha; 28 } 29 int main(){ 30 scanf("%d",&n); 31 int root=1; 32 for(int i=1;i<=n;++i){ 33 int x,y,m; 34 scanf("%d%d%d",&x,&y,&m); 35 val[x]=y; 36 int son=0; 37 for(int j=1;j<=m;++j){ 38 scanf("%d",&son); 39 if(son==root) root=x; 40 Add(x,son); 41 } 42 } 43 dfs(root); 44 // printf("%d ",root); 45 printf("%d ",min(dp[root][0],dp[root][2])); 46 return 0; 47 }
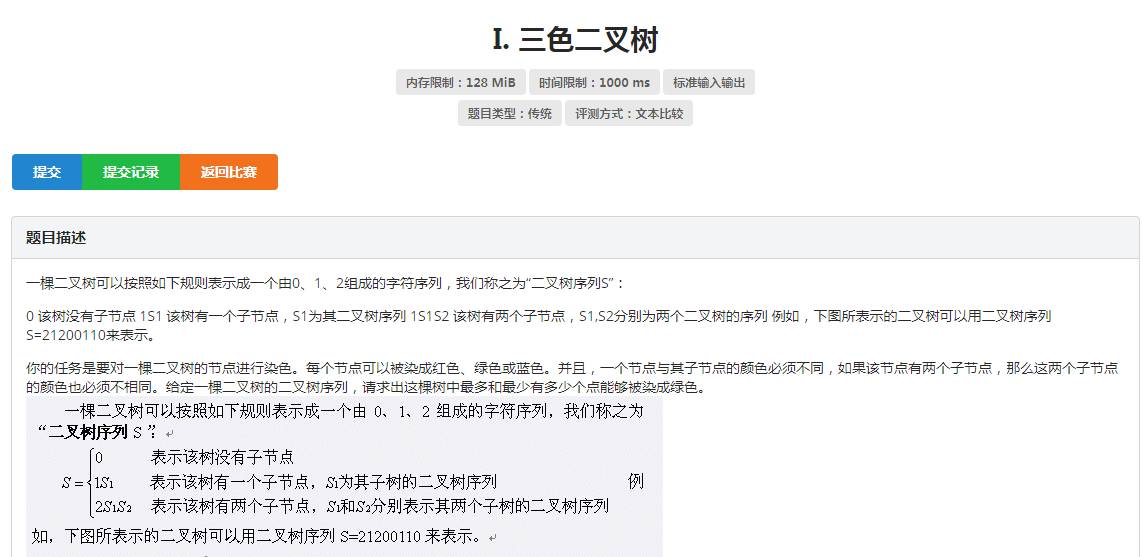
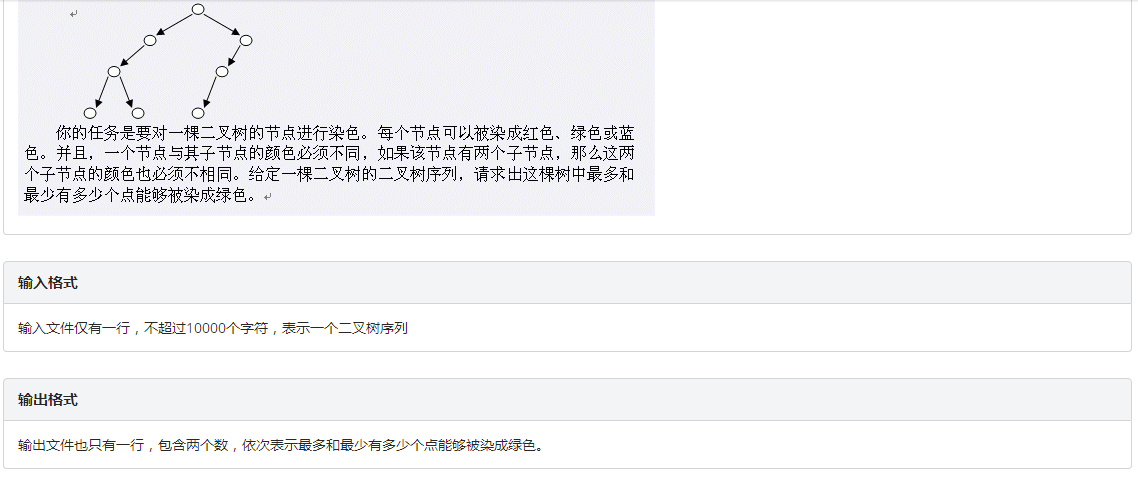
特别骄傲的说,这道题是我自己不看题解写出来的,成就感满满呀。
分析:这道题给你的除绿色意外的两种颜色没什么卵用,把他们看作一种颜色就好了,如果父节点为绿色,他的答案就是两个节点都不是绿色的答案和,如果不是绿色,那么答案就是两个子节点分别是绿色,不是绿色两种情况取最优即可,这里我用到了一个k滚动的方法,省了一些for循环,最后就是开始的建树过程,可能比较繁琐,但并不难,用一个栈维护即可。
代码:

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<stack> 5 #include<vector> 6 using namespace std; 7 const int N=6e5+10; 8 int val[N],dp[N][2],fa[N],ans,tot=1,now=1; 9 stack<int>q; 10 vector<int>edge[N]; 11 void dfs1(int u){ 12 dp[u][1]=1; 13 for(int i=0;i<edge[u].size();++i){ 14 int v=edge[u][i]; 15 dfs1(v); 16 dp[u][1]+=dp[v][0]; 17 if(edge[u].size()==1) dp[u][0]+=max(dp[v][0],dp[v][1]); 18 } 19 if(edge[u].size()==2){ 20 bool k=0; 21 int Max=-1; 22 for(int j=1;j<=2;++j){ 23 k=!k;dp[u][0]=0; 24 for(int i=0;i<edge[u].size();++i){ 25 int v=edge[u][i]; 26 k=!k; 27 dp[u][0]+=dp[v][k]; 28 } 29 Max=max(Max,dp[u][0]); 30 } 31 dp[u][0]=Max; 32 } 33 } 34 void dfs2(int u){ 35 dp[u][1]=1; 36 for(int i=0;i<edge[u].size();++i){ 37 int v=edge[u][i]; 38 dfs2(v); 39 dp[u][1]+=dp[v][0]; 40 if(edge[u].size()==1) dp[u][0]+=min(dp[v][0],dp[v][1]); 41 } 42 if(edge[u].size()==2){ 43 bool k=0; 44 int Min=0x3f3f3f3f; 45 for(int j=1;j<=2;++j){ 46 k=!k;dp[u][0]=0; 47 for(int i=0;i<edge[u].size();++i){ 48 int v=edge[u][i]; 49 k=!k; 50 dp[u][0]+=dp[v][k]; 51 } 52 Min=min(Min,dp[u][0]); 53 } 54 dp[u][0]=Min; 55 } 56 } 57 int main(){ 58 //freopen("a.in","r",stdin); 59 char ch; 60 while(true){ 61 ch=getchar(); 62 int t=ch-'0'; 63 if(t==0){ 64 if(q.empty()) break; 65 else{ 66 now=q.top();q.pop(); 67 } 68 } 69 else if(t==1){ 70 edge[now].push_back(++tot); 71 //printf("%d->%d ",now,tot); 72 now=tot; 73 } 74 else if(t==2){ 75 edge[now].push_back(++tot); 76 //printf("%d->%d ",now,tot); 77 edge[now].push_back(++tot); 78 //printf("%d->%d ",now,tot); 79 q.push(tot); 80 now=tot-1; 81 } 82 } 83 //printf("%d ",edge[2].size()); 84 dfs1(1); 85 //for(int i=1;i<=tot;++i) 86 // printf("%d %d ",dp[i][1],dp[i][0]); 87 printf("%d ",max(dp[1][1],dp[1][0])); 88 memset(dp,0,sizeof(dp)); 89 dfs2(1); 90 printf("%d ",min(dp[1][1],dp[1][0])); 91 return 0; 92 }
关于最后一道题:我就是个zz,这是之前的分享题呀,怎么就忘了那?滚回去看自己写的博客去[https://www.cnblogs.com/li-jia-hao/p/12650241.html]。
第一天总结:除了下午的突袭考试之外,还是比较顺的,上午帮回家的同学们搬书手都要瘸了,现在还疼(其实今天已经是第二天了),无论怎样,我们的第一次信息集训算是顺利地拉开了帷幕,教练说我们在这几天内会发生质变,让现在写蓝题都要看题解的我很期待自己将来能不能成为一名神犇呢。
