题目描述
B君在围观一群男生和一群女生玩游戏,具体来说游戏是这样的:
给出一棵n个节点的树,这棵树的每条边有一个权值,这个权值只可能是0或1。 在一局游戏开始时,会确定一个节点作为根。接下来从女生开始,双方轮流进行 操作。
当一方操作时,他们需要先选择一个不为根的点,满足该点到其父亲的边权为1; 然后找出这个点到根节点的简单路径,将路径上所有边的权值翻转(即0变成1,1 变成0 )。
当一方无法操作时(即所有边的边权均为0),另一方就获得了胜利。
如果在双方均采用最优策略的情况下,女生会获胜,则输出“Girls win!”,否则输 出“Boys win!”。
为了让游戏更有趣味性,在每局之间可能会有修改边权的操作,而且每局游戏指 定的根节点也可能是不同的。
具体来说,修改边权和进行游戏的操作一共有m个,具体如下:
∙“0 x”表示询问对于当前的树,如果以x为根节点开始游戏,哪方会获得胜利。
∙“1 x y z ”表示将x和y之间的边的边权修改为z。
B君当然知道怎么做啦!但是他想考考你。
Input
包含至多5组测试数据。
第一行有一个正整数,表示数据的组数。
接下来每组数据第一行,有二个空格隔开的正整数n,m,分别表示点的个数,操 作个数。保证n,m< 40000。
接下来n-1行,每行三个整数x,y,z,表示树的一条边。保证1<x<n, 1<y< n, 0 <= z <= 1。
接下来m行,每行一个操作,含义如前所述。保证一定只会出现前文中提到的两 种格式。
对于操作0,保证1 <= x <= n ;对于操作1,保证1 <= x <= n, 1 <= y <= n, 0 <= z <= 1,保证树上存在一条边连接x和y。
Output
对于每组数据的每一个询问操作,输出一行“Boys win!”或者“Girls win!”。
Sample Input
2 2 3 1 2 0 0 1 1 2 1 1 0 2 4 11 1 2 1 2 3 1 3 4 0 0 1 0 2 0 3 0 4 1 2 1 0 0 1 0 2 0 3 1 3 4 1 0 3 0 4
Sample Output
Boys win! Girls win! Girls win! Boys win! Girls win! Boys win! Boys win! Girls win! Girls win! Boys win! Girls win!
思路分析:
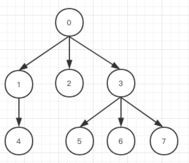
关于这道题我们可以考虑,设如果当前要反转的节点不是与当前游戏的根相连的话,在一方操作完之后,该节点上方所有的边的边权都会
发生翻转,例如下图所示,我们设3-7初始边权为1,0-3为0,在翻转完7号节点之后,0-3之间的边权变为了1,则之后后手可以继续翻转3
号节点以复原除3-7外其他被修改的边权,这就相当于我们以把一条边权为1的边变为0为代价将游戏的当前操作方又变回了原来的先手。那么
若这么考虑下去,先手必输。
但我们还需要考虑,后手要翻转边是有条件的,及该边与其父节点的边权为1,即1.有父节点,2.边权为1.
在先手翻完一条边后,后手应该从先手所翻转的点向上找到第一个可以翻转的点进行复原,但如果上面的点是根节点的话,后手将无法操作,
只好从一条新的树边开始,那么此时先手边掌握了主动权,直到再次遇到一条与根相连边权为1的点为止。如果主动权变换次数为偶数了话,
最终还是后手,即男孩赢,反之女孩赢。那么对于每个节点,只需统计与他相连的且边权为1的节点个数,当为偶数时,boy win,反之,
girl win。最后注意修改即可。
附上代码

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 const int N=1e6+10; 5 int Head[N],tot,sum[N]; 6 struct Node{ 7 int next,to,dis; 8 }edge[N]; 9 void Add(int x,int y,int z){ 10 edge[++tot].to=y; 11 edge[tot].next=Head[x]; 12 edge[tot].dis=z; 13 Head[x]=tot; 14 } 15 void update(int x,int y,int z){ 16 for(int i=Head[x];i;i=edge[i].next){ 17 int v=edge[i].to; 18 if(v==y){ 19 if(edge[i].dis==z) return; //如果修改值相同就不用改了. 20 else if(z){ 21 sum[x]++; 22 edge[i].dis++; 23 } 24 else{ 25 sum[x]--; 26 edge[i].dis--; 27 } 28 return; 29 } 30 } 31 } 32 void work(){ 33 int x; 34 scanf("%d",&x); 35 if(sum[x]%2==0) printf("Boys win! "); 36 else printf("Girls win! "); 37 } 38 int main(){ 39 int T; 40 scanf("%d",&T); 41 while(T--){ 42 memset(Head,0,sizeof(Head)); //多组数据需要更新。 43 memset(edge,0,sizeof(edge)); 44 memset(sum,0,sizeof(sum)); 45 tot=0; 46 int n,m; 47 scanf("%d%d",&n,&m); 48 for(int i=1;i<n;++i){ 49 int x,y,z; 50 scanf("%d%d%d",&x,&y,&z); 51 Add(x,y,z);Add(y,x,z); //加边建树 52 sum[x]+=z;sum[y]+=z; //统计相连且边权为1个数 53 } 54 for(int i=1;i<=m;++i){ 55 int t; 56 scanf("%d",&t); 57 if(t){ 58 int x,y,z; 59 scanf("%d%d%d",&x,&y,&z); 60 update(x,y,z);update(y,x,z); //进行更新 61 } 62 else work(); 63 } 64 } 65 return 0; 66 }