题目描述


输入格式

输出格式

思路分析:
这道题的题意简单来说就是两点之间的边权就是从0到n-1的值之中,从u到v到唯一路径(因为是树)不经过的值之中的最小值,题目最后要求算出从所有一点到所有另一点的所有权值之和的最大值。显然我们可以贪心,我们让权值小的边尽可能多的在任意两点之间的线段上,这样就能使最多的边的边权之和尽可能大。由于0最小,我们便把它安排在图的中央,则可以使两边的点互通使都过0(原因:0的这条边将图分为两部分,设这个图共有n个点,0将图分为大小为x和y的两部分,则互通过0的边数为x*y,则我们要求x*y的最大值,根据数学知识可得当x尽可能等于y时x*y最大,即0尽可能在图的中央)在安排完0之后,我们开始思考下一条边的位置,还是刚才括号内的原因,故越小的边越应该往中间凑,故1应该在0的旁边。
看一下从liuchang大佬那里白嫖的图
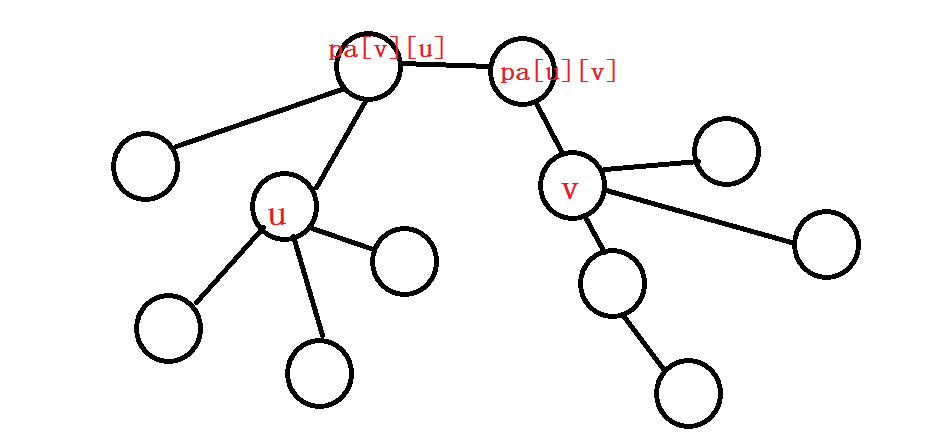
我们先跑n遍DFS,用sum[i][u]求出以i为根时u节点的子树大小,用pa[i][v]表示以i为根时v节点的父亲,先把0放在中央,权值为0的边的两边元素分别为u,v,则此时sum[u]*sum[v]个边同时过0,此时它们的权值都为1(1尚未进入图中),即答案值加上sum[u]*sum[v],之后我们既可以把1接在(u,pa[u][v])间,也可在 (v,pa[v][u])之间,此时sum[u]*sum[v]的部分边的权值由于过了1而发生改变,变为了2,由于它们的权值已经是1,最终结果再加上一个sum[u]*sum[v](u,v均已变为权值为1的两端节点),这相当与我们把大小n的大问题拆为了大小x和大小y的子问题,于是在统计答案时想到递归处理.最后记得要开long long
附上代码
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int N=5e3+10; 6 typedef long long ll; 7 int Head[N],tot,n,m; 8 struct Node{ 9 int next,to; 10 }edge[N]; 11 void Add(int x,int y){ 12 edge[++tot].to=y; 13 edge[tot].next=Head[x]; 14 Head[x]=tot; 15 } 16 ll dp[N][N]; //dp最终答案可能很大,要开long long 17 int sum[N][N],pa[N][N]; 18 void dfs(int rt,int u,int fa){ //初始化pa,sum 19 sum[rt][u]=1; 20 for(int i=Head[u];i;i=edge[i].next){ 21 int v=edge[i].to; 22 if(v==fa) continue; 23 dfs(rt,v,u); 24 sum[rt][u]+=sum[rt][v]; 25 pa[rt][v]=u; 26 } 27 } 28 ll Dp(int u,int v){ //递归进行答案计算 29 if(u==v) return 0; 30 if(dp[u][v]) return dp[u][v]; 31 return dp[u][v]=max(Dp(u,pa[u][v]),Dp(v,pa[v][u]))+sum[u][v]*sum[v][u]; 32 } 33 int main(){ 34 scanf("%d",&n); 35 for(int i=1;i<n;++i){ 36 int x,y; 37 scanf("%d%d",&x,&y); 38 Add(x,y);Add(y,x); 39 } 40 for(int i=1;i<=n;++i){ 41 dfs(i,i,0); //分别初始化每一个点 42 } 43 ll ans=-1; 44 for(int i=1;i<=n;++i){ 45 for(int j=1;j<=n;++j) 46 ans=max(ans,Dp(i,j)); //寻找答案 47 } 48 printf("%lld ",ans); 49 return 0; 50 }