Emergency Evacuation（贪心）

题目描述（中文版）

　　                                                                                       紧急疏散
                                                                                          时间限制：3秒
日本政府计划到2020年将入境游客人数增加到4000万，到2030年增加到6000万。不仅要增加游客的吸引力，而且要进一步发展旅游基础设施对于实现这一数字是必不可少的。
运输方面的一种可能的改进是提供极长和/或较宽的汽车，一次可搭载多名乘客。但是，太大的汽车可能需要太长时间才能在紧急情况下疏散所有乘客。请您帮助估计所需的时间。
假定汽车具有以下座椅布置。
•中央过道直通汽车，直接连接到汽车后部中央的紧急出口门。
•乘客座位数相同的行位于过道的两侧。
要求的粗略估算基于简单的逐步模型。最初，所有乘客都坐在不同的座位上，他们可以在每个步骤中进行以下任一动作。
•座位上的乘客可以朝过道移动到相邻的座位。与过道相邻的座位上的乘客可以直接向侧面移动到过道。
•过道上的乘客可以向后移动一排座位。如果乘客在紧急出口的前面，即在最后面的座位排，他/她可以下车。
要移动的座位或过道位置必须为空；或者在该步骤之前没有其他乘客在这里，或者该乘客通过在同一步骤中移至另一个位置来清空座位。当两个或两个以上的乘客满足同一位置的条件时，他们中只有一个可以移动，而其他人则保持在原来的位置等待。
图C.1的最左图描绘了样本输入1中给出的小型汽车的座椅布置。该汽车有五排座椅，在过道两侧各有两个座椅，共二十个。还显示了船上七名乘客的初始位置。
图C.1的另外两个图显示了第一步和第二步之后乘客的可能位置。乘客的移动由粗箭头指示。请注意，前排座位中的两名乘客必须在第一步中等待空缺，而第二排中的一名乘客必须在下一步中等待。
您的任务是编写一个程序，在给定座位安排和乘客初始位置的情况下，为所有乘客下车提供尽可能少的步骤。

错误的思路分析

　　我上来看到这道题的第一印象就是模拟人们下车的过程，当时没有考虑时间效率，就调出来了一个极其难看的代码，跑的还贼慢。大家感兴趣的可以看看我的笨蛋思路。

1. 在考虑下车时,由于开始时过道两边可能都有人坐,我们就要考虑是左边先下还是右边先进过道的问题

我们便可以假设有如图的一种情况,我们设他们相邻过道上的位置距离出口d，则三个点无论以什么样的顺序出，最终耗时都为（d+1）+（d+1）+（d+2）即3d+4个单位时间，所以相邻过道两边的先后进入过道的顺序与最终答案无关。

2. 若出现如下图的情况，红色的人应该先插入过道还是待一列人走完后从末尾跟着走（有颜色代表有人）

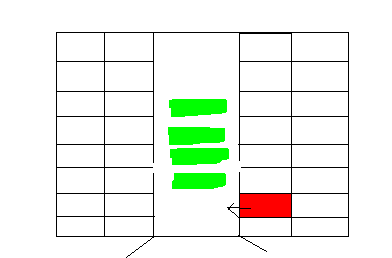
我们可以假设红色在前面，则该五个人出去所需的总时间为7个单位时间，而让红色跟在后面，则需要8个单位时间，故如果在过道边坐着的人如果可以进入过道的话就让优先进入过道。

则我们最终模拟的顺序为先让能进入过道的人先进过道，再让中间的还没动过的人向下走，最后往中间移得动的人向中间动，这是一次移动，最后计数即可。

弄上代码

#include<cstdio>
#include<cstring>
#include<algorithm>
const int N=500;
const int maxn=N*N;
struct People{  //People保存每个人的位置（x，y），是否下车（chu） 
    int x,y;    // 本轮是否移动(ok) 
    bool chu,ok;
}pe[N];
int a[N][N];    //存储车的平面图. 
int id[N][N];   //存储每个位置的编号 
int r,s,p,mid;
int ans=0;
int main(){
    scanf("%d%d%d",&r,&s,&p);
    int mid=s+1;
    for(int i=1;i<=p;++i){
        int x,y;
        scanf("%d%d",&x,&y);
        if(y>=mid) y++;
        a[x][y]=1;
        id[x][y]=i;
        pe[i].x=x;pe[i].y=y;
    }
    int cnt=p;
    while(cnt){
        for(int i=1;i<=p;++i)   //每轮更新 
            pe[i].ok=0;
        for(int i=1;i<=p;++i){   //可以进过道的进过道 
            if(pe[i].y==s&&!a[pe[i].x][mid]){
                int x=pe[i].x,y=pe[i].y;
                a[x][y]=0;a[x][y+1]=1;
                pe[i].y++;id[x][y+1]=id[x][y];id[x][y]=0;
                pe[i].ok=1;
            }
            if(pe[i].y==s+2&&!a[pe[i].x][mid]){
                int x=pe[i].x,y=pe[i].y;
                a[x][y]=0;a[x][y-1]=1;
                pe[i].y--;id[x][y-1]=id[x][y];id[x][y]=0;
                pe[i].ok=1;
            }
        }
        for(int i=r;i>=1;--i){   //过道可以往下走的往下走. 
            int t=id[i][mid];
            if(!t||pe[t].chu) continue;
            if(pe[t].ok) continue;
            if(i==r){
                pe[t].chu=true;a[i][mid]=0;
                cnt--;
            }
            else if(a[i+1][mid]) continue;
            a[i+1][mid]=1;a[i][mid]=0;
            pe[t].x=i+1;pe[t].ok=1;
            id[i+1][mid]=id[i][mid];id[i][mid]=0;
        }
        for(int i=1;i<=p;++i){  //两边可以向中间靠的向中间靠. 
            int x=pe[i].x,y=pe[i].y;
            if(pe[i].chu) continue;
            if(y==mid) continue;
            if(y<mid){
                if(a[x][y+1]) continue;
                a[x][y+1]=1;a[x][y]=0;id[x][y+1]=id[x][y];id[x][y]=0;
                pe[i].ok=true;pe[i].y=y+1;
                while(a[x][y-1]&&!pe[id[x][y-1]].ok){
                    if(y>=mid||y<1) break;
                    a[x][y-1]=0;a[x][y]=1;id[x][y]=id[x][y-1];id[x][y-1]=0;
                    pe[id[x][y]].ok=true;pe[id[x][y]].y++;
                    y--;
                }
            }
            if(y>mid){
                if(a[x][y-1]) continue;
                a[x][y-1]=1;a[x][y]=0;id[x][y-1]=id[x][y];id[x][y]=0;
                pe[i].ok=true;pe[i].y--;
                while(a[x][y+1]&&!pe[id[x][y+1]].ok){
                    if(y<=mid||y>2*s+1) break;
                    a[x][y+1]=0;a[x][y]=1;id[x][y]=id[x][y+1];id[x][y+1]=0;
                    pe[id[x][y]].ok=true;pe[id[x][y]].y--;
                    y++;
                }
            }
        }
        ans++;  //统计次数 
    }
    printf("%d
",ans);
    return 0;
}

如果你这样写了，恭喜你，由于超时你一个点都过不了。

下面才是正确思路及写法

我们可以逆序考虑，既然求下车的最大时间，我们可以转化为每个人都在车下，先后上车到他的座位，求出上车最慢的等待时间即可。每个人的时间开销为上车时间+等待时间，则根据贪心的思想，我们可以对每个人的上车时间进行排序，时间花销大的先上车，最后将每个人的上车时间和等待时间之和取最大值即可。（每个人的时间开销即从座位到出口的距离）

附上代码

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=500005;
struct People{ //保存每个人的位置,及距出口的距离. 
    int r,c;
    int d;
}pe[N];
bool cmp(People a,People b){
    return a.d>b.d;
} 
int main(){
    int r,s,p;
    scanf("%d%d%d",&r,&s,&p);
    for(int i=1;i<=p;++i){
        scanf("%d%d",&pe[i].r,&pe[i].c);
        if(pe[i].c>s)   //计算距离,横向加竖向. 
            pe[i].d=(pe[i].c-s)+(r-pe[i].r+1);
        else
            pe[i].d=(s-pe[i].c+1)+(r-pe[i].r+1);    
    }
    sort(pe+1,pe+1+p,cmp);
    int k=1;  //k用于计算每个人的等待时间 
    int max_time=pe[1].d;
    for(int i=2;i<=p;++i){
        if(pe[i].d+k>max_time)
            max_time=pe[i].d+k;  //计算最大时间开销 
        k++;
    }
    printf("%d
",max_time);
    return 0;
}

正确写法及思路来自https://blog.csdn.net/qq_40534166/article/details/88894175?depth_1-utm_source=distribute.pc_relevant.none-task-blog-OPENSEARCH-1&utm_source=distribute.pc_relevant.none-task-blog-OPENSEARCH-1