呀,图真是一个令人头疼而又很重要的东西。在现实生活中,我们有很多的问题都不能用树来实现,所以烦人啊不伟大的图就出现了——
图的存储
没有存储哪来的操作,所以存储是最基础的呢。
邻接矩阵
我们对于图的存储需要存储顶点和边的信息,最简单的就是邻接矩阵的方法了。
如果我们想要存储这样的一张图
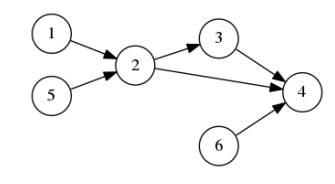
就可以使用到我们的好伙伴二维数组来帮忙了,具体点来说,如果有一张有 N 个点的图,那么我们就可以使用 N×N 的二维数组来存储。数组的每个元素的值代表了对应的边的数量。就像这个样子——
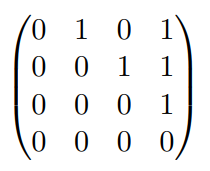
这样可以很方便快捷地存储一些很稠密的图,而且可以很快速地定位到某条边。
代码长这样——
1 scanf("%d",&n); 2 for(int i = 1; i <= n; i++){ 3 scanf("%d%d",&x,&y); 4 a[x][y] = a[y][x] = 1;//无向图,x->y和y->x都要存 5 }
*敲代码的时候注意有向图和无向图^=^
权矩阵
若边有权,就用A[i,j]存储边<i,j>的权。若没有边则默认无穷大。
代码长这样——
1 scanf("%d",&n); 2 memset(a,0x3f,sizeof(a)); 3 for(int i = 1; i <= n; i++){ 4 scanf("%d%d%d",&x,&y,&w); 5 a[x][y] = a[y][x] = w; 6 }
我们用邻接矩阵存图的时候需要开一个二维数组来存边,空间会很大,更适合一些稠密图。对于一些点多边少的图,空间和时间的代价也会随之增加,所以我们需要设计一个数据结构用来记录与其相连的边之间的联系。
So,我们优秀的代表邻接表就出现了——
邻接表
(小声BB:虽然我们老师一直叫它链式前向星,但我一直没明白前向星是什么东东)
邻接表把与顶点相连的所有边依次来拿成一条链,并新建一个元素在定点与这条链的开端建立一个联系,这样我们可以通过顶点的初始链接访问到与这个顶点相连的第一条边,再沿着这条链依次往后访问下一条边。(此文出自CCF中学生计算机程序设计提高篇P77)
当然它也可以用来存树。
代码长这样——
1 struct edge{ 2 int to,nxt,w; 3 }e[10000]; 4 5 void addedge(int u,int v){ 6 e[++tot].to=v; 7 e[tot].nxt=head[u]; 8 e[tot].w = w;//存权~ 9 head[u]=tot; 10 }
看着有点神奇,其实也没有那么复杂,手动模拟一下就能明白了。
首先我们假设我们有这样的一张图——
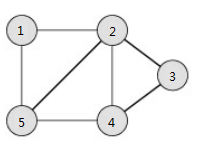
一共7条边(u,v):
① 1 --> 2 ⑤ 2 --> 4
② 1 --> 5 ⑥ 2 --> 3
③ 2 --> 5 ⑦ 3 --> 4
④ 4 --> 5
我们需要几个东西:
tot 用来记录有几条边
e[] 用来记录边与点与边之间的关系
head[] 用来记录点最后一条存储的边的序号
首先我们先把所有的数组值初始化为-1
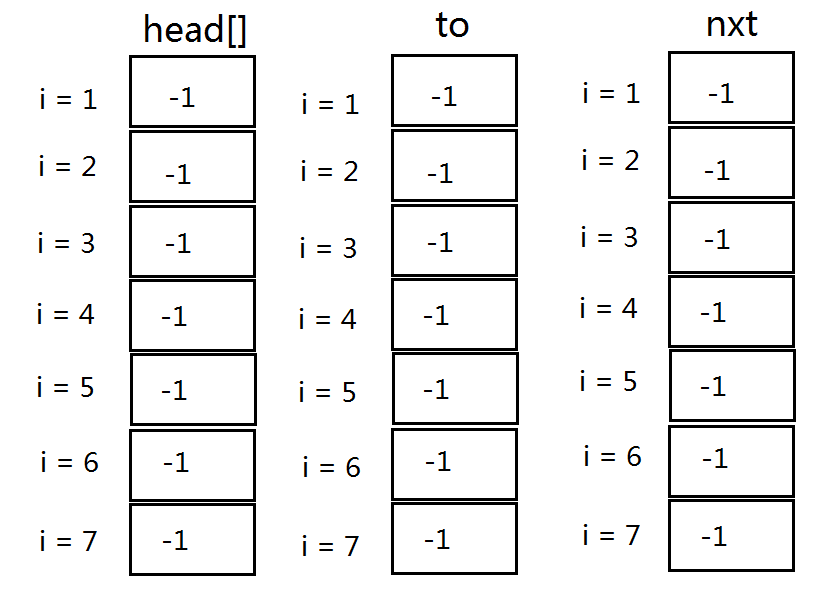
存第一条边 ① 1 --> 2时,tot = 1
就会变成这样——
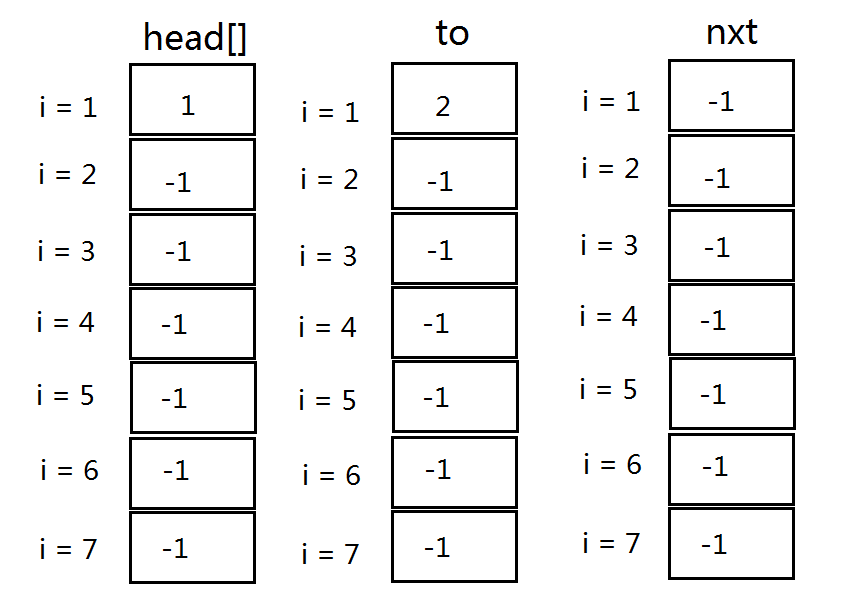
存第二条边 ② 2 --> 4,tot = 2
就会变成这样——
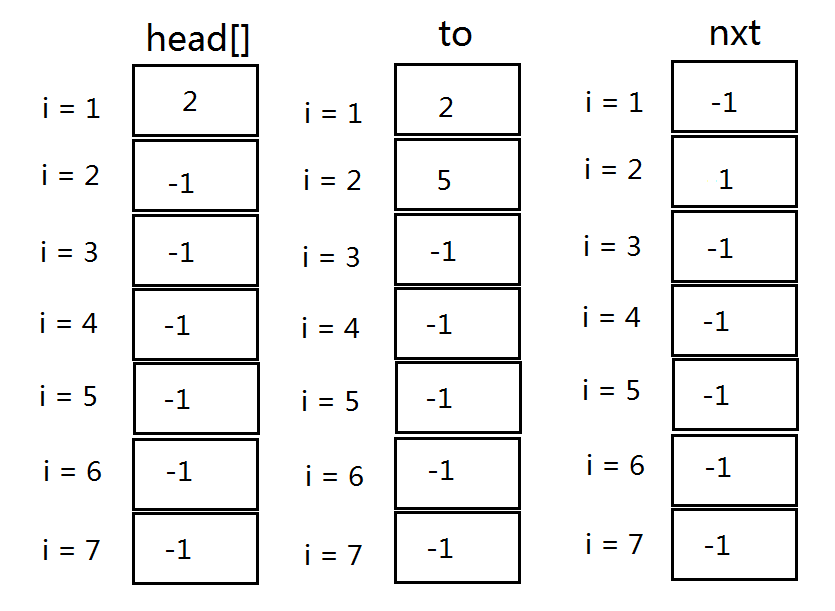
将它们全部模拟一遍就会变成这个样子——

(应该没错吧)
然后我们就巧妙地获得了点与边之间的关系,那应该怎么运用呢?那就是图的遍历啦~
图的遍历
邻接矩阵没什么好讲的啦,循环一遍就OK。我们重点来talk about邻接表
我们刚刚经过一系列的折腾操作得到了点与边之间的联系,当然得好好地利用啊。
当我们想从 u 点遍历整张图or树时,让 i 指向 head[u],如果 i != -1,i 就可以指向 e[i].nxt 去寻找下一条边。
代码长这样——
1 void dfs(int u){ 2 vis[u] = 1;//搜过了标记一下,无向图以防重复搜,树以防搜到它爸爸 3 for(int i = head[u]; i; i = e[i].nxt){ 4 int v = e[i].to; 5 if(vis[v]) continue; 6 dfs(v); 7 } 8 }
这样子我们就可以顺着一个个点一条条边有序地遍历一整张图,如果还不清晰的话就自己手动模拟一遍吧。
这种做法我第一次知道的时候感觉它特别神奇,几个看不出什么关系的数(也可能是我太菜了)竟然可以让我们遍历整张图。
事实证明它确实很好用(多半是学校老师逼得),但这并不影响我对它初见面时惊讶的看法。
相信你们肯定也能体会到它的好处的~
总结一下
图是个挺重要的东西,把一张图用几个数字所记录,对于我来说是把具体变成抽象,是个不小的挑战。
写这篇东西主要是想多巩固巩固基础,也希望大家看了之后能有收获。
拜拜~
(如果文章有不对的地方,请指出,谢谢啦^=^)