概念
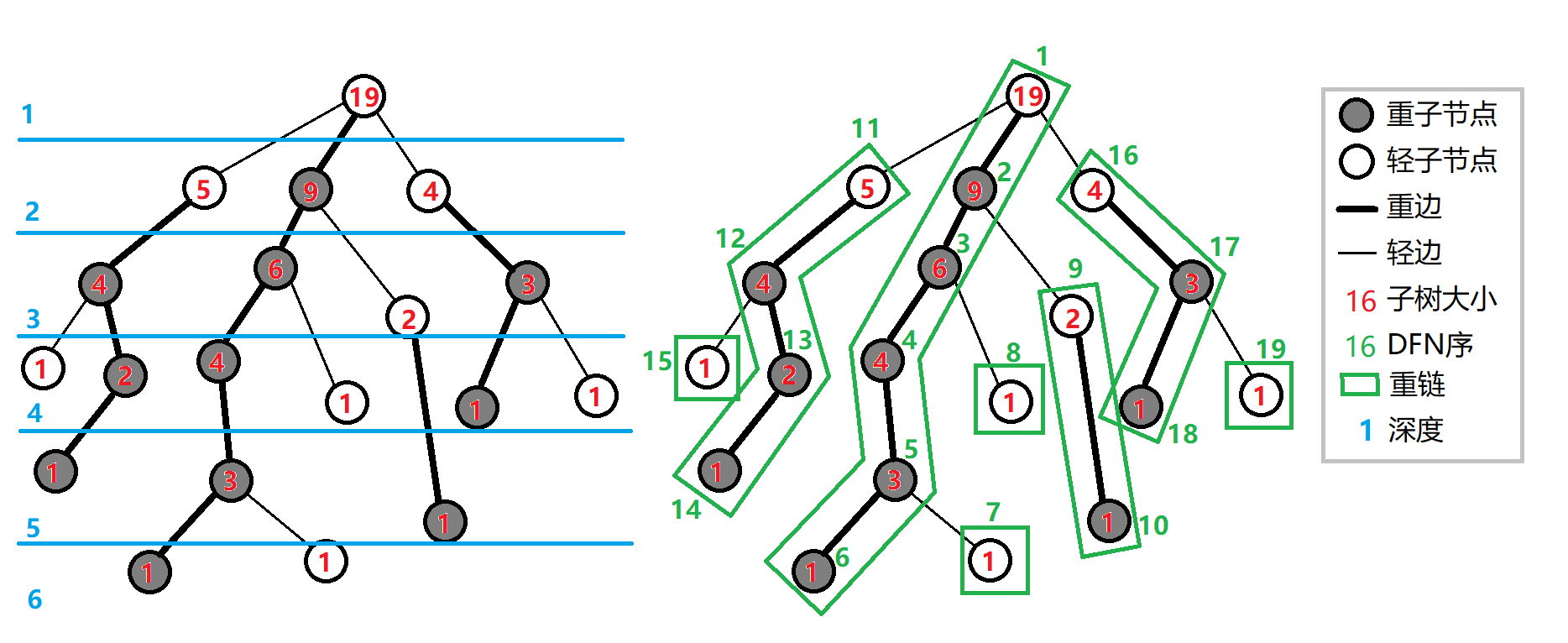
长链剖分按深度剖分,重儿子为叶子最深的儿子。具体应用时可以通过指针记录信息,也可以优先遍历重儿子来 (dfs),链上信息为一个在 (dfs) 序上的连续区间,便于统计信息和将信息从重儿子合并过来。
void dfs_son(int x,int fa)
{
d[x]=dep[x]=d[fa]+1;
for(int i=head[x];i;i=e[i].nxt)
{
int y=e[i].to;
if(y==fa) continue;
dfs_son(y,x),dep[x]=max(dep[x],dep[y]);
if(dep[y]>dep[son[x]]) son[x]=y;
}
len[x]=dep[x]-d[x];
}
一个节点到根节点的轻边个数是 (sqrt n) 级别的。
树上 k 级祖先
可以做到 (O(1)) 查询树上 (k) 级祖先。对于每个长度为 (len) 的链,预处理链顶端向上 (len) 个节点,和沿链向下 (len) 个节点,其为即链上的点。询问时先树上倍增,跳到 (2^i) 级祖先,满足 (2^i leqslant k <2^{i+1}),对于 (2^i) 级祖先所在的链,满足 (k-2^i < 2^i < len),所以可以跳到所在的链顶端后再通过预处理的信息来调整。
void dfs_son(int x)
{
de[x]=dep[x]=de[f[x][0]]+1;
for(int i=1;i<=19;++i) f[x][i]=f[f[x][i-1]][i-1];
for(int i=head[x];i;i=e[i].nxt)
{
int y=e[i].to;
dfs_son(y),dep[x]=max(dep[x],dep[y]);
if(dep[y]>dep[son[x]]) son[x]=y;
}
}
void dfs_dfn(int x,int tp,int anc)
{
top[x]=tp,dfn[x]=++cnt,u[cnt]=anc,d[cnt]=x;
if(son[x]) dfs_dfn(son[x],tp,f[anc][0]);
for(int i=head[x];i;i=e[i].nxt)
{
int y=e[i].to;
if(y==son[x]) continue;
dfs_dfn(y,y,y);
}
}
int ask(int x,int k)
{
if(!k) return x;
x=f[x][lg[k]],k-=(1<<lg[k])+de[x]-de[top[x]],x=top[x];
if(k>=0) return u[dfn[x]+k];
else return d[dfn[x]-k];
}
优化 DP
对于形如状态为 (f_{x,i}) ,(i) 那一维是关于深度的树形 (DP),可以通过长链剖分来优化。每次转移时先从重儿子来继承,对轻儿子扫一遍其所在的链,因为每个轻儿子都是其所在链的顶端,所以每个点只会被扫一遍。