首先考虑题目的性质,发现点向区间连的边为双向边,所以也就可以从一个点向右跳到区间包含该点的点,如图所示:
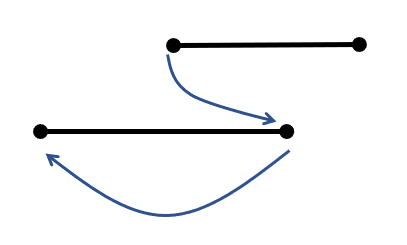
但事实上向后跳其实是不优的,可以有更好的方法来节省花费:

因此我们发现一个点跳到其前一个区间的花费为 (1),且在跳跃过程中不会向右跳,同时我们还证明了一个点向左的花费单调递增。
但是从起点进行第一步跳跃时,有可能会向后跳:

其通过向后跳来到达一个更大的包含该点的区间,然后使下一步跳跃到达一个更向前的位置,第一步采取向后跳方案的花费为 (2)。
发现只有第一步是特殊的,所以单独来考虑第一步的情况。
设 (pos_i=minlimits_{j=i}^n l_j),即 (l_i) 的后缀最小值,(pos_i) 即为位置 (i) 第一步采取向后跳方案来到达的最向前的位置。
对每个位置建可持久化线段树,线段树中对应的值为该位置不考虑第一步的花费,位置 (i) 的线段树从位置 (pos_i) 转移过来,然后在区间 ([1,i-1]) 通过标记永久化来实现区间加一,表示不是第一步跳的花费。
查询时只需在 (l_x) 所对应的线段树上查询区间 ([l,min(r,l_x-1)]) 的和,其为位置 (x) 除去第一步的总花费,然后再加上第一步花费的贡献即可。
(code:)
#include<bits/stdc++.h>
#define maxn 300010
#define maxm 10000010
#define mid ((l+r)>>1)
using namespace std;
typedef long long ll;
template<typename T> inline void read(T &x)
{
x=0;char c=getchar();bool flag=false;
while(!isdigit(c)){if(c=='-')flag=true;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
if(flag)x=-x;
}
int n,q,tot;
int a[maxn],pos[maxn],rt[maxn],ls[maxm],rs[maxm];
ll sum[maxm],add[maxm];
ll gcd(ll a,ll b)
{
return b?gcd(b,a%b):a;
}
void modify(int L,int R,int l,int r,int &cur)
{
int x=++tot;
ls[x]=ls[cur],rs[x]=rs[cur],add[x]=add[cur];
sum[x]=sum[cur]+(min(R,r)-max(L,l)+1),cur=x;
if(L<=l&&R>=r)
{
add[cur]++;
return;
}
if(L<=mid) modify(L,R,l,mid,ls[cur]);
if(R>mid) modify(L,R,mid+1,r,rs[cur]);
}
ll query(int L,int R,int l,int r,int cur)
{
if(L>R) return 0;
if(L<=l&&R>=r) return sum[cur];
ll v=add[cur]*(min(R,r)-max(L,l)+1);
if(L<=mid) v+=query(L,R,l,mid,ls[cur]);
if(R>mid) v+=query(L,R,mid+1,r,rs[cur]);
return v;
}
int main()
{
read(n);
for(int i=2;i<=n;++i) read(a[i]),pos[i]=a[i];
for(int i=n-1;i>=2;--i) pos[i]=min(pos[i],pos[i+1]);
for(int i=2;i<=n;++i) rt[i]=rt[pos[i]],modify(1,i-1,1,n,rt[i]);
read(q);
while(q--)
{
int l,r,x;
ll g,v;
read(l),read(r),read(x),v=r-l+1;
v+=query(l,min(r,a[x]-1),1,n,rt[a[x]]);
g=gcd(v,r-l+1),printf("%lld/%lld
",v/g,(r-l+1)/g);
}
return 0;
}