先考虑对题目进行转化,我们称两个区间有交集为这两个区间能匹配,每个询问就是在序列中最长能连续匹配的长度。
对序列中的一个区间([l,r])和询问的一个区间([L,R]),若满足(L leqslant r)且(l leqslant R),那么这两个区间是能匹配的。
可以将一个区间用点来表示,然后用(K-D Tree)来维护所有的询问区间,序列区间按顺序一个个去更新每个询问的匹配信息即可。
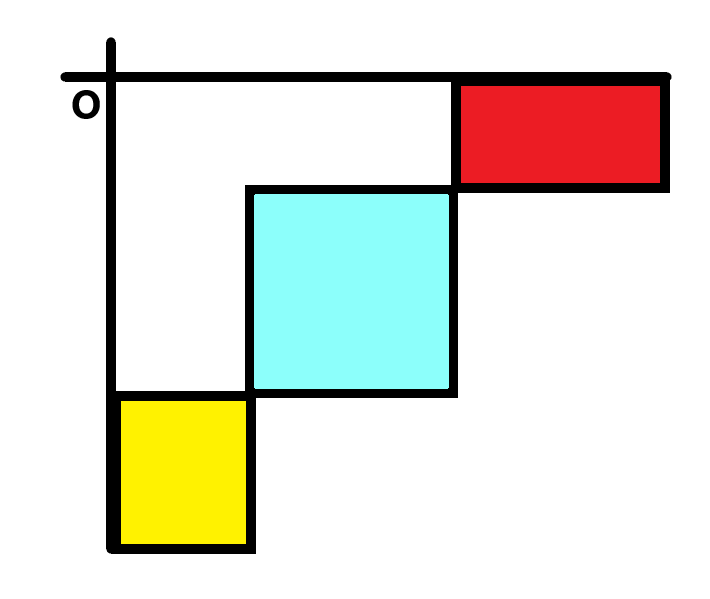
对(K-D Tree)中的维护一个矩形来考虑,比如下图的蓝色矩形为这个矩形。
当一个点落在红色矩形时,那么该点和矩形内的所有点都能匹配,对该矩形打上加法标记,使矩形内所有点的当前匹配数加一。
当一个点落在黄色矩形时,那么该点和矩形内的所有点都不能匹配,对该矩形打上清零标记,使矩形内所有点的当前匹配数清零。
同时记录一个点在整个过程中的历史最大匹配数,其即为最终一个点所对应询问的答案。
对一个矩形清空后,还会进行一系列对其匹配数增加的操作,但此时打上加法标记是错误的,所以给它打上一个赋值标记,打标记时增加赋值标记即可,同时记录下这阶段赋值标记的历史最大值,并用其去更新该点的历史最大匹配数。
标记比较多,有很多细节,具体实现看代码吧。
(code:)
#include<bits/stdc++.h>
#define maxn 400010
using namespace std;
template<typename T> inline void read(T &x)
{
x=0;char c=getchar();bool flag=false;
while(!isdigit(c)){if(c=='-')flag=true;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
if(flag)x=-x;
}
int n,m,root,tot,type;
int cov[maxn],his[maxn],add[maxn],tag[maxn];
int ans[maxn],ma[maxn],cnt[maxn];
struct node
{
int l,r;
}p[maxn];
struct KD_tree
{
int d[2],mi[2],ma[2],ls,rs,id;
}t[maxn],dat[maxn];
bool cmp(const KD_tree &a,const KD_tree &b)
{
return a.d[type]<b.d[type];
}
void pushup(int x)
{
int ls=t[x].ls,rs=t[x].rs;
for(int i=0;i<=1;++i)
{
t[x].ma[i]=t[x].mi[i]=t[x].d[i];
if(ls)
{
t[x].ma[i]=max(t[x].ma[i],t[ls].ma[i]);
t[x].mi[i]=min(t[x].mi[i],t[ls].mi[i]);
}
if(rs)
{
t[x].ma[i]=max(t[x].ma[i],t[rs].ma[i]);
t[x].mi[i]=min(t[x].mi[i],t[rs].mi[i]);
}
}
}
void update(int x,int v)
{
cnt[x]+=v,ma[x]=max(ma[x],cnt[x]);
}
void pushadd(int x,int v)
{
update(x,v);
if(cov[x]) tag[x]+=v,his[x]=max(his[x],tag[x]);
else add[x]+=v;
}
void pushcov(int x)
{
if(!cov[x]) cov[x]=1,his[x]=0;
cnt[x]=tag[x]=0;
}
void pushtag(int x,int v1,int v2)
{
cov[x]=1,his[x]=max(his[x],v2);
cnt[x]=tag[x]=v1,ma[x]=max(ma[x],his[x]);
}
void pushdown(int x)
{
int ls=t[x].ls,rs=t[x].rs;
if(add[x])
{
pushadd(ls,add[x]),pushadd(rs,add[x]);
add[x]=0;
}
if(cov[x])
{
pushtag(ls,tag[x],his[x]),pushtag(rs,tag[x],his[x]);
cov[x]=tag[x]=0;
}
}
void build(int l,int r,int k,int &x)
{
x=++tot,type=k;
int mid=(l+r)>>1;
nth_element(dat+l+1,dat+mid+1,dat+r+1,cmp);
t[x]=dat[mid];
if(l<mid) build(l,mid-1,k^1,t[x].ls);
if(r>mid) build(mid+1,r,k^1,t[x].rs);
pushup(x);
}
bool in(KD_tree tr,int l,int r)
{
return tr.ma[0]<=r&&l<=tr.mi[1];
}
bool out(KD_tree tr,int l,int r)
{
return tr.mi[0]>r||l>tr.ma[1];
}
void modify(int x,int l,int r)
{
int ls=t[x].ls,rs=t[x].rs;
if(in(t[x],l,r))
{
pushadd(x,1);
return;
}
if(out(t[x],l,r))
{
pushcov(x);
return;
}
pushdown(x);
if(t[x].d[0]<=r&&l<=t[x].d[1]) update(x,1);
else cnt[x]=0;
if(ls) modify(ls,l,r);
if(rs) modify(rs,l,r);
}
void dfs(int x)
{
int ls=t[x].ls,rs=t[x].rs;
pushdown(x),ans[t[x].id]=ma[x];
if(ls) dfs(ls);
if(rs) dfs(rs);
}
int main()
{
read(n),read(m);
for(int i=1;i<=n;++i) read(p[i].l),read(p[i].r);
for(int i=1;i<=m;++i)
read(dat[i].d[0]),read(dat[i].d[1]),dat[i].id=i;
build(1,m,0,root);
for(int i=1;i<=n;++i) modify(root,p[i].l,p[i].r);
dfs(root);
for(int i=1;i<=m;++i) printf("%d
",ans[i]);
return 0;
}